Envelope Detection in MATLAB
This example shows how to implement two common methods of envelope detection. One method uses squaring and lowpass filtering. The other uses the Hilbert transform. For a similar example in Simulink™, see Envelope Detection in Simulink.
Introduction
The signal envelope is equivalent to its outline, and an envelope detector connects all the peaks in this signal. Envelope detection has numerous applications in the fields of signal processing and communications, one of which is amplitude modulation (AM) detection. The following block diagram shows the implementation of the envelope detection using the two methods.

Method 1: Squaring and Lowpass Filtering
This envelope detection method involves squaring the input signal and sending it through a lowpass filter. Squaring the signal effectively demodulates the input by using the signal as its own carrier wave, which means that half the energy of the signal is pushed up to higher frequencies and half is shifted down toward DC. You then downsample this signal to reduce the sampling frequency. You can downsample if the signal does not have any high frequencies that can cause aliasing. Otherwise you must use FIR decimation, which applies a lowpass filter before downsampling the signal. After this step, pass the signal through a minimum-phase lowpass filter to eliminate the high-frequency energy, and you are left with only the signal envelope.
To maintain the correct scale, you must perform two additional operations. First, you must amplify the signal by a factor of two. Since you are keeping only the lower half of the signal energy, this gain matches the final energy to its original energy. Second, you must take the square root of the signal to reverse the scaling distortion that resulted from squaring the signal.
This envelope detection method is easy to implement and can be performed using a low-order filter, which minimizes the lag of the output.
Method 2: The Hilbert Transform
This envelope detection method involves creating an analytic signal of the input using the Hilbert transform. An analytic signal is a complex signal, where the real part is the original signal and the imaginary part is the Hilbert transform of the original signal.
Mathematically, the envelope e(t) of a signal x(t) is defined as the magnitude of the analytic signal as shown by the following equation.
where is the Hilbert transform of .
You can find the Hilbert transform of the signal using a 32-point Parks-McClellan FIR filter. To form the analytic signal, you then multiply the Hilbert transform of the signal by sqrt(-1) (the imaginary unit) and add it to the time-delayed original signal. It is necessary to delay the input signal because the Hilbert transform, which is implemented by an FIR filter, introduces a delay equal to half the filter length.
You find the envelope of the signal by taking the absolute value of the analytic signal. The envelope is a low frequency signal compared to the original signal. To reduce its sampling frequency, to eliminate ringing and to smooth the envelope, you downsample this signal and pass the result through a lowpass filter.
Initialization
Specify the sample rate, number of samples, downsample factor, and frame size.
Fs = 22050; numSamples = 10000; DownsampleFactor = 15; frameSize = 10*DownsampleFactor;
Creating and initializing your System objects before they are used in a processing loop is critical for getting optimal performance. Create a sine wave System object™ and set its properties to generate two sine waves. One sine wave acts as the message signal and the other sine wave as the carrier signal to produce amplitude modulation.
sine = dsp.SineWave([0.4 1],[10 200], ... SamplesPerFrame=frameSize, ... SampleRate=Fs);
Create a lowpass FIR filter for filtering the squared signal to detect its envelope.
lp1 = dsp.FIRFilter(Numerator=firpm(20,[0 0.03 0.1 1],[1 1 0 0]));
Create three digital filter System objects. The first implements the Hilbert transformer, the second compensates for the delay introduced by the Hilbert transformer, and the third is a lowpass filter for detecting the signal envelope.
N = 60; % Filter order hilbertTransformer = dsp.FIRFilter( ... Numerator=firpm(N,[0.01 .95],[1 1],"hilbert")); delay = dsp.Delay(Length=N/2); lp2 = dsp.FIRFilter(Numerator=firpm(20,[0 0.03 0.1 1],[1 1 0 0]));
Create and configure two time scope System objects to plot the input signal and its envelope.
scope1 = timescope( ... Name="Envelope detection using Amplitude Modulation", ... SampleRate=[Fs,Fs/DownsampleFactor], ... TimeDisplayOffset=[(N/2+frameSize)/Fs,0], ... TimeSpan=0.45, ... YLimits=[-2.5 2.5]); pos = scope1.Position; scope2 = timescope( ... Name="Envelope detection using Hilbert Transform", ... Position=[pos(1)+pos(3),pos(2:4)], ... SampleRate=[Fs,Fs/DownsampleFactor], ... TimeDisplayOffset=[(N/2+frameSize)/Fs,0], ... TimeSpan=0.45, ... YLimits=[-2.5 2.5]);
Stream Processing Loop
Create the processing loop to perform envelope detection on the input signal. This loop uses the System objects you instantiated in the previous section.
for i = 1:numSamples/frameSize sig = sine(); sig = (1 + sig(:,1)) .* sig(:, 2); % Amplitude modulation % Envelope detector by squaring the signal and lowpass filtering sigsq = 2 * sig .* sig; sigenv1 = sqrt(lp1(downsample(sigsq,DownsampleFactor))); % Envelope detector using the Hilbert transform in the time domain sige = abs(complex(0, hilbertTransformer(sig)) + delay(sig)); sigenv2 = lp2(downsample(sige,DownsampleFactor)); % Plot the signals and envelopes scope1(sig,sigenv1); scope2(sig,sigenv2); end release(scope1);
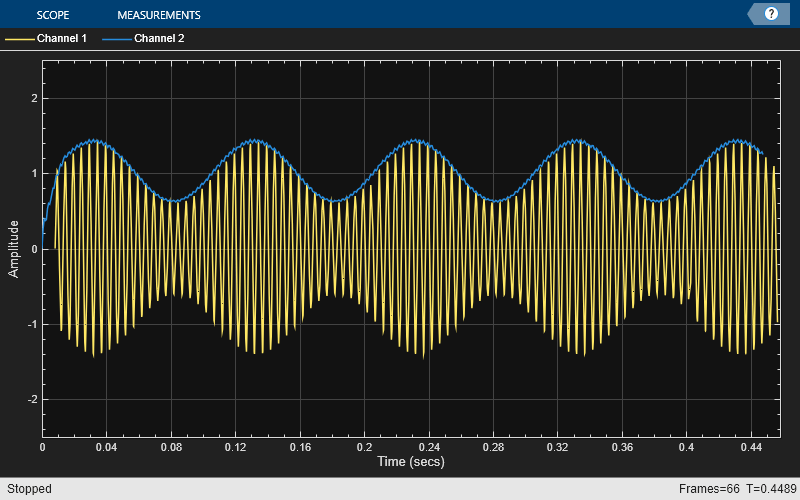
release(scope2);
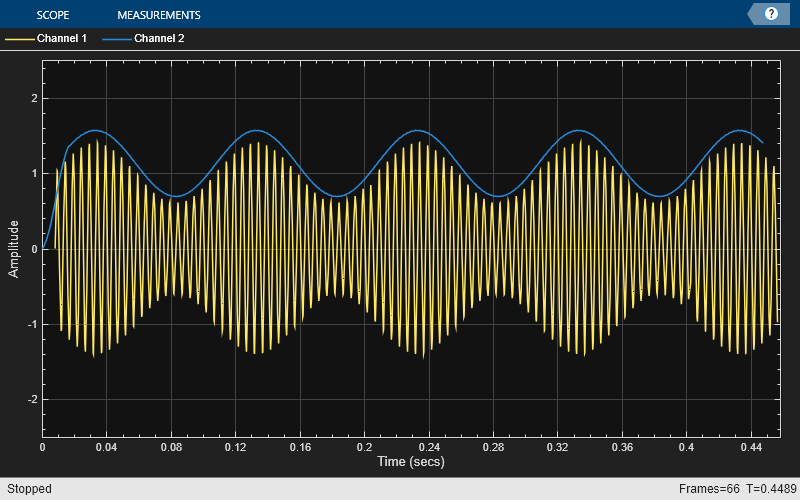
Envelope Detector Results
In the plots, for the envelope detection method using Hilbert transform, the envelope amplitude does not match the actual signal because the Hilbert transform that you implemented using the FIR filter is not ideal as its magnitude response does not equal 1 for all frequencies. The shape of the envelope still matches the envelope of the actual signal.
See Also
dsp.SineWave | dsp.FIRFilter | timescope