MATLAB での包絡線検出
この例では、包絡線検出を実装する 2 種類の一般的な方法を説明します。1 つは、2 乗とローパス フィルター処理を使用する方法です。もう 1 つは、ヒルベルト変換を使用する方法です。Simulink™ の同様の例については、Envelope Detection in Simulinkを参照してください。
はじめに
信号の包絡線は信号の外枠に等しく、包絡線検出器はこの信号のすべてのピークを接続します。包絡線検出は信号処理と通信の分野に多くの用途がありますが、その 1 つに振幅変調 (AM) 検出があります。2 つの方法を使用した包絡線検出の実装を次のブロック線図に示します。

メソッド 1: 2 乗とローパス フィルター処理
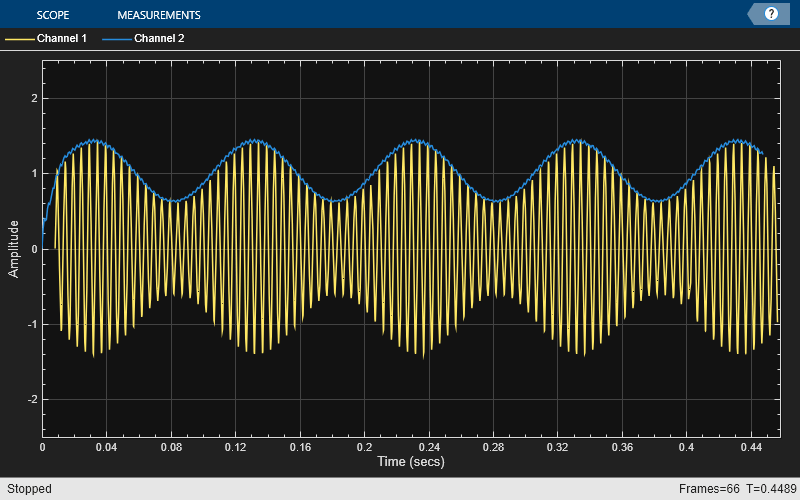
この包絡線検出方法では、入力信号を 2 乗して、それをローパス フィルターに送信します。信号を 2 乗する場合は、信号をそれ自体の搬送波として使用することで入力が実質的に復調されます。つまり、信号のエネルギーの半分は高い周波数に押し上げられ、残りの半分は DC に向かって下にシフトします。次にこの信号をダウンサンプリングして、サンプリング周波数を下げます。ダウンサンプリングは、信号に、エイリアシングを起こす可能性がある高周波数がない場合に行うことができます。それ以外の場合は、信号をダウンサンプリングする前に FIR 間引きを使用してローパス フィルターを適用しなければなりません。この手順の後で最小位相のローパス フィルターから信号を渡し、高周波数エネルギーを除去します。これにより信号の包絡線のみが残ります。
正しいスケールを保つために、2 つの操作を追加しなければなりません。最初にファクター 2 で信号を増幅しなければなりません。低周波数側の半分の信号エネルギーのみを保持しているため、このゲインにより最終エネルギーが元のエネルギーに一致します。次に、信号の平方根を求めて、信号を 2 乗したときに生じたスケーリングの歪みを反転します。
この包絡線検出方法は実装が簡単で低次数フィルターで実行できるため、出力のラグを最小限に抑えることができます。
メソッド 2: ヒルベルト変換
この包絡線検出方法では、ヒルベルト変換を使用して入力の解析信号を作成します。解析信号は複素数信号であり、実数部は元の信号で、虚数部は元の信号のヒルベルト変換です。
数学的には、信号 x(t) の包絡線 e(t) は、次の方程式に示される解析信号の振幅として定義されます。
ここで、 は のヒルベルト変換です。
信号のヒルベルト変換は、32 点 Parks-McClellan FIR フィルターを使用して求めます。解析信号を形成するには、信号のヒルベルト変換に sqrt(-1) (虚数単位) を乗算し、これを時間遅延した元の信号に加算します。FIR フィルターによって実装されるヒルベルト変換により、フィルター長の半分に等しい遅延が生じるため、入力信号の遅延が必要になります。
信号の包絡線は、解析信号の絶対値を使用して検出できます。包絡線は元の信号より低い周波数信号です。サンプリング周波数を減らし、リンギングを除去して滑らかな包絡線を得るには、この信号をダウンサンプリングして結果をローパス フィルターから渡します。
初期化
サンプル レート、サンプル数、ダウンサンプリング係数、およびフレーム サイズを指定します。
Fs = 22050; numSamples = 10000; DownsampleFactor = 15; frameSize = 10*DownsampleFactor;
処理ループで使用する前に System object を作成して初期化することは、最適なパフォーマンスを得るために不可欠です。正弦波 System object™ を作成し、2 つの正弦波を生成するようにプロパティを設定します。1 つの正弦波はメッセージ信号として動作し、もう 1 つの正弦波は搬送波として振幅変調を生成します。
sine = dsp.SineWave([0.4 1],[10 200], ... SamplesPerFrame=frameSize, ... SampleRate=Fs);
方形の信号をフィルター処理して包絡線を検出するために、ローパス FIR フィルターを作成します。
lp1 = dsp.FIRFilter(Numerator=firpm(20,[0 0.03 0.1 1],[1 1 0 0]));
デジタル フィルター System object を 3 つ作成します。最初のオブジェクトはヒルベルト変換器を実装し、2 番目のオブジェクトはヒルベルト変換器によって導入された遅延を補正し、3 番目のオブジェクトは信号の包絡線を検出するためのローパス フィルターです。
N = 60; % Filter order hilbertTransformer = dsp.FIRFilter( ... Numerator=firpm(N,[0.01 .95],[1 1],"hilbert")); delay = dsp.Delay(Length=N/2); lp2 = dsp.FIRFilter(Numerator=firpm(20,[0 0.03 0.1 1],[1 1 0 0]));
2 つの Time Scope System object を作成し、入力信号と包絡線をプロットするように設定します。
scope1 = timescope( ... Name="Envelope detection using Amplitude Modulation", ... SampleRate=[Fs,Fs/DownsampleFactor], ... TimeDisplayOffset=[(N/2+frameSize)/Fs,0], ... TimeSpan=0.45, ... YLimits=[-2.5 2.5]); pos = scope1.Position; scope2 = timescope( ... Name="Envelope detection using Hilbert Transform", ... Position=[pos(1)+pos(3),pos(2:4)], ... SampleRate=[Fs,Fs/DownsampleFactor], ... TimeDisplayOffset=[(N/2+frameSize)/Fs,0], ... TimeSpan=0.45, ... YLimits=[-2.5 2.5]);
ストリーム処理ループ
入力信号で包絡線検出を実行する処理ループを作成します。このループは前のセクションでインスタンス化した System object を使用します。
for i = 1:numSamples/frameSize sig = sine(); sig = (1 + sig(:,1)) .* sig(:, 2); % Amplitude modulation % Envelope detector by squaring the signal and lowpass filtering sigsq = 2 * sig .* sig; sigenv1 = sqrt(lp1(downsample(sigsq,DownsampleFactor))); % Envelope detector using the Hilbert transform in the time domain sige = abs(complex(0, hilbertTransformer(sig)) + delay(sig)); sigenv2 = lp2(downsample(sige,DownsampleFactor)); % Plot the signals and envelopes scope1(sig,sigenv1); scope2(sig,sigenv2); end release(scope1);
release(scope2);
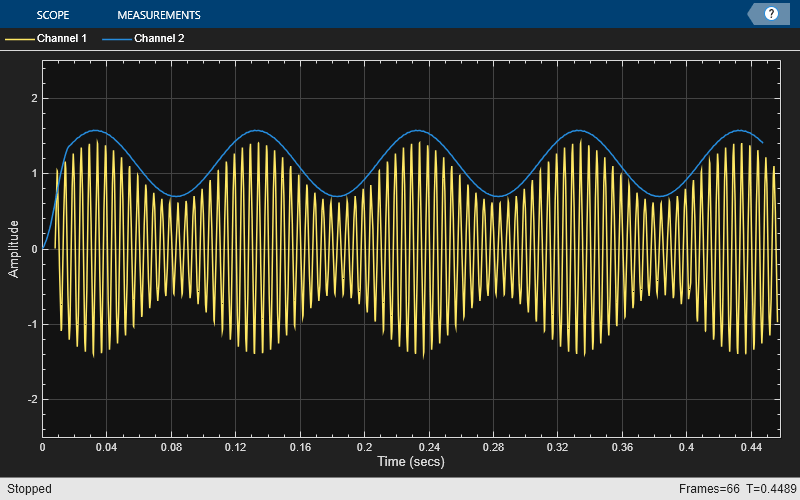
包絡線検出器結果
ヒルベルト変換を使用した包絡線検出方法のプロットでは、包絡線の振幅が実際の信号に一致しません。これは、FIR フィルターを使用して実装したヒルベルト変換では振幅応答がすべての周波数で 1 に等しくなるとは限らないため、理想値を得ることができないためです。包絡線の形状は実際の信号の包絡線に一致しています。
参考
dsp.SineWave | dsp.FIRFilter | timescope