ディープネットワークデザイナーを使用した時系列予測ネットワークの構築

この例では、ディープネットワークデザイナーアプリを使用して、時系列データを予測するためのシンプルな長短期記憶 (LSTM) ネットワークを作成する方法を示します。

LSTM ネットワークは、タイムステップ全体にわたってループ処理して RNN の状態を更新することにより入力データを処理する再帰型ニューラルネットワーク (RNN) です。RNN の状態には、前のすべてのタイムステップで記憶された情報が含まれています。LSTM ニューラルネットワークを使用して、前のタイムステップを入力として使用して、時系列またはシーケンスの後続の値を予測できます。時系列予測用の LSTM ネットワークを作成するには、ディープネットワークデザイナーアプリを使用します。

以下の Figure は、閉ループ予測を使用した予測値のシーケンスの例を示しています。

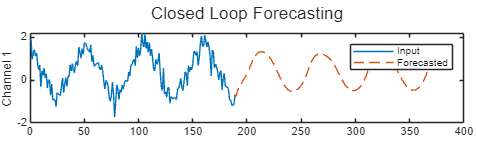
シーケンスデータの読み込み

サンプルデータを WaveformData から読み込みます。このデータにアクセスするには、例をライブスクリプトとして開きます。この波形データセットには、3 つのチャネルの異なる波長の合成生成波形が格納されています。この例では、前のタイムステップからの値を与えて波形の将来の値を予測するように LSTM ニューラルネットワークに学習させます。

load WaveformData

最初のいくつかのシーケンスのサイズを表示します。

data(1:4)

ans=4×1 cell array
    {103×3 double}
    {136×3 double}
    {140×3 double}
    {124×3 double}

チャネル数を表示します。LSTM ニューラルネットワークに学習させるには、各シーケンスのチャネル数が同じでなければなりません。

numChannels = size(data{1},2)

numChannels = 3

シーケンスの一部を可視化します。

idx = 1;
numChannels = size(data{idx},2);

figure
stackedplot(data{idx},DisplayLabels="Channel " + (1:numChannels))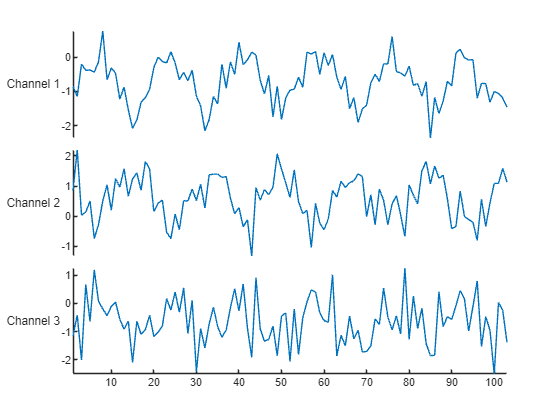

学習用データの準備

シーケンスの将来のタイムステップの値を予測するには、1 タイムステップ分シフトした値を持つ学習シーケンスとしてターゲットを指定します。学習シーケンスには最終タイムステップを含めないでください。つまり、入力シーケンスの各タイムステップで、次のタイムステップの値を予測するように LSTM ニューラルネットワークに学習させます。予測子は、最後のタイムステップを含まない学習シーケンスです。

numObservations = numel(data);
XData = cell(numObservations,1);
TData = cell(numObservations,1);
for n = 1:numObservations
    X = data{n};
    XData{n} = X(1:end-1,:);
    TData{n} = X(2:end,:);
end

データを学習セット、検証セット、テストセットに分割します。データの 80% は学習に使用し、10% は検証に使用し、10% はテストに使用します。データを分割するには、この例にサポートファイルとして添付されている関数 trainingPartitions を使用します。このファイルにアクセスするには、例をライブスクリプトとして開きます。

[idxTrain,idxValidation,idxTest] = trainingPartitions(numObservations,[0.8 0.1 0.1]);

XTrain = XData(idxTrain);
TTrain = TData(idxTrain);

XValidation = XData(idxValidation);
TValidation = TData(idxValidation);

XTest = XData(idxTest);
TTest = TData(idxTest);

良好な適合を実現し、学習の発散を防ぐには、チャネルがゼロ平均と単位分散をもつように予測子とターゲットを正規化します。予測を行うときは、学習データと同じ統計を使用して検証データとテストデータも正規化しなければなりません。

シーケンスについて、チャネルごとの平均値と標準偏差値を計算します。学習データの平均と標準偏差を簡単に計算するには、関数 cell2mat を使用して、連結されたシーケンスを含む数値配列を作成します。

muX = mean(cell2mat(XTrain));
sigmaX = std(cell2mat(XTrain),0);

muT = mean(cell2mat(TTrain));
sigmaT = std(cell2mat(TTrain),0);

計算された平均値と標準偏差値を使用して学習データを正規化します。

for n = 1:numel(XTrain)
    XTrain{n} = (XTrain{n} - muX) ./ sigmaX;
    TTrain{n} = (TTrain{n} - muT) ./ sigmaT;
end

学習データから計算された統計を使用して、検証データとテストデータを正規化します。

for n = 1:numel(XValidation)
    XValidation{n} = (XValidation{n} - muX) ./ sigmaX;
    TValidation{n} = (TValidation{n} - muT) ./ sigmaT;
end

for n = 1:numel(XTest)
    XTest{n} = (XTest{n} - muX) ./ sigmaX;
    TTest{n} = (TTest{n} - muT) ./ sigmaT;
end

ネットワークアーキテクチャの定義

ネットワークを構築するには、ディープネットワークデザイナーアプリを開きます。

deepNetworkDesigner

シーケンスネットワークを作成するには、[シーケンスネットワーク] セクションの [Sequence-to-Sequence] で、[開く] をクリックします。

これにより、シーケンス分類の問題に適したプリビルドネットワークが開きます。ネットワークには以下の層が含まれています。

sequenceInputLayer
lstmLayer
dropoutLayer
fullyConnectedLayer
softmaxLayer

最終層を編集することで、分類ネットワークを時系列予測に適したネットワークに変換できます。まず、ソフトマックス層を削除します。

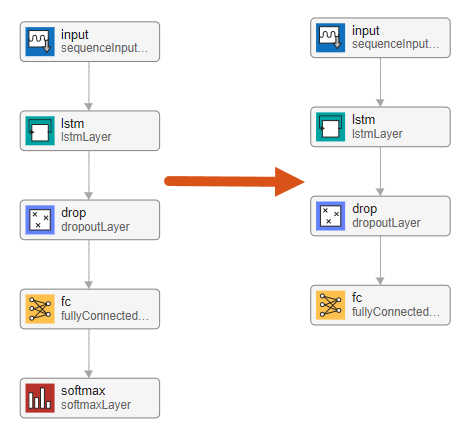
次に、波形データセットに適するように層のプロパティを調整します。時系列の将来のデータ点を予測することが目的なので、出力サイズは入力サイズと同じでなければなりません。この例では、入力データに 3 つの入力チャネルがあるため、ネットワーク出力にも 3 つの出力チャネルがなければなりません。

シーケンス入力層 input を選択し、[InputSize] を 3 に設定します。

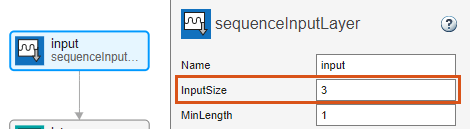
全結合層 fc を選択し、[OutputSize] を 3 に設定します。

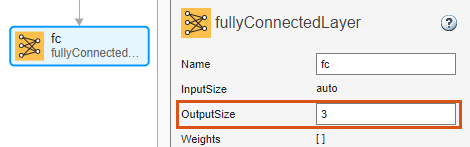
LSTM 層は 128 個の隠れユニットをもちます。隠れユニットの数によって、層に学習させる情報量が決まります。より多くの隠れユニットを使用するほど正確な結果が得られますが、学習データの過適合につながる可能性が高くなります。ドロップアウト層は、層への入力をランダムにゼロに設定し、学習の反復間でネットワークアーキテクチャを効果的に変更することにより、過適合の回避を支援します。ドロップアウトの確率が高いと、情報が失われ、学習プロセスが遅くなりますが、モデルの汎化は促進されます。

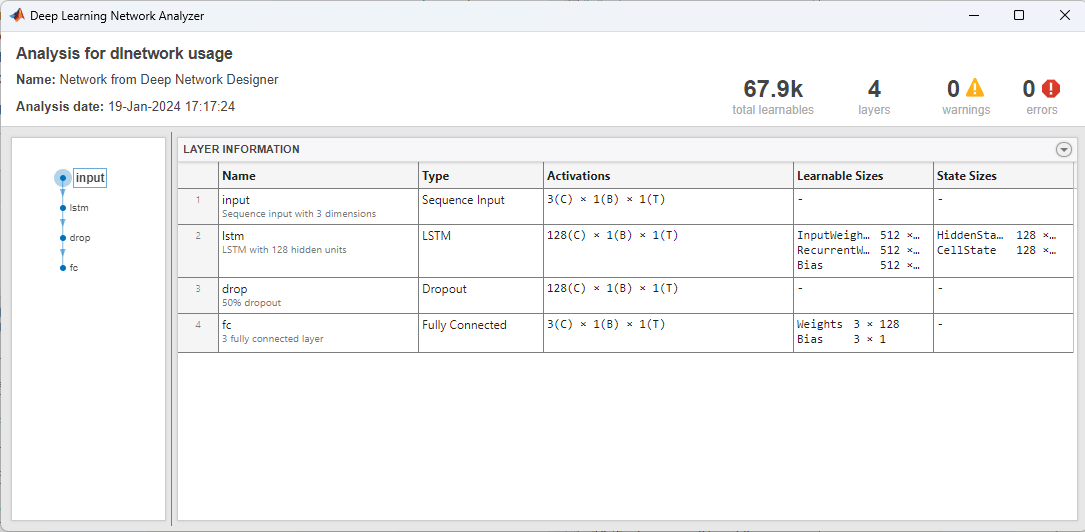
ネットワークの学習の準備が整っていることを確認するには、[解析] をクリックします。深層学習ネットワークアナライザーによってエラーや警告が報告されていないため、ネットワークの学習の準備は整っています。ネットワークをエクスポートするには、[エクスポート] をクリックします。アプリはネットワークを変数 net_1 に保存します。

学習オプションの指定

学習オプションを指定します。オプションの中から選択するには、経験的解析が必要です。実験を実行してさまざまな学習オプションの構成を調べるには、実験マネージャーアプリを使用できます。

Adam 最適化を使用して学習させます。
学習を 200 エポック行います。より大きなデータセットでは、良好な適合を実現させるために多くのエポックを学習させる必要がない場合があります。
各ミニバッチでシーケンスを左パディングし、シーケンスが同じ長さになるようにします。左パディングにより、シーケンスの最後にパディングされた値を RNN が予測することを防ぎます。
すべてのエポックでデータをシャッフルします。
検証データを使用して過適合を監視します。
平方根平均二乗誤差を監視します。
学習の進行状況をプロットに表示します。
詳細出力を無効にします。

options = trainingOptions("adam", ...
    MaxEpochs=200, ...
    SequencePaddingDirection="left", ...
    Shuffle="every-epoch", ...
    ValidationData={XValidation,TValidation}, ...
    Metrics="rmse", ...
    Plots="training-progress", ...
    Verbose=false);

ニューラルネットワークの学習

関数trainnetを使用して LSTM ニューラルネットワークに学習させます。回帰の場合は、平均二乗誤差損失を使用します。既定では、関数 trainnet は利用可能な GPU がある場合にそれを使用します。GPU を使用するには、Parallel Computing Toolbox™ ライセンスとサポートされている GPU デバイスが必要です。サポートされているデバイスについては、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。そうでない場合、関数は CPU を使用します。実行環境を指定するには、ExecutionEnvironment 学習オプションを使用します。

net = trainnet(XTrain,TTrain,net_1,"mse",options);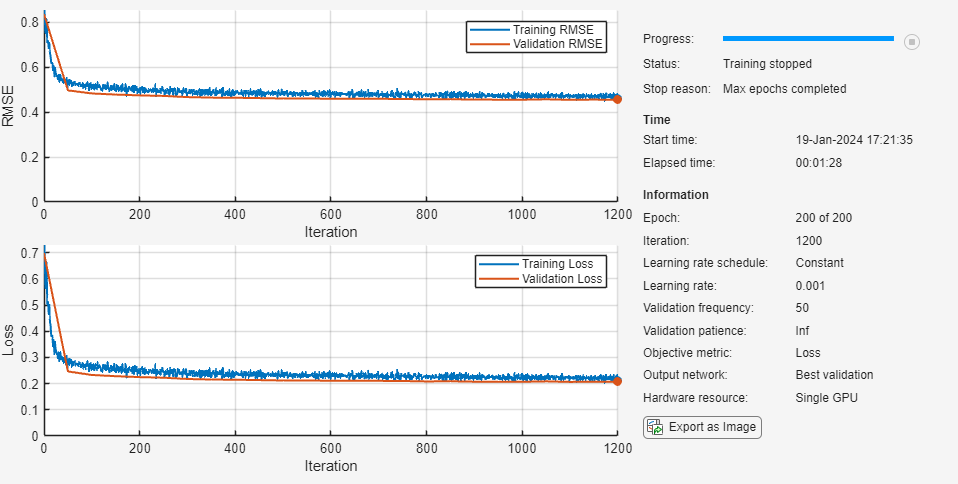

再帰型ニューラルネットワークのテスト

関数minibatchpredictを使用して予測を行います。既定では、関数 minibatchpredict は利用可能な GPU がある場合にそれを使用します。学習の場合と同じパディングオプションを使用してシーケンスをパディングします。さまざまな長さのシーケンスを含む sequence-to-sequence タスクでは、UniformOutput オプションを false に設定して、予測を cell 配列として返します。

YTest = minibatchpredict(net,XTest, ...
    SequencePaddingDirection="left", ...
    UniformOutput=false);

各テストシーケンスについて、予測とターゲットの間の平方根平均二乗誤差 (RMSE) を計算します。RMSE を計算する前にパディング値を削除して、すべてのパディング値を無視します。

numObservationsTest = numel(XTest);

for n = 1:numObservationsTest
    
    T = TTest{n};
    sequenceLength = size(T,1);
    Y = YTest{n}(end-sequenceLength+1:end,:);

    err(n) = rmse(Y,T,"all");
end

ヒストグラムで誤差を可視化します。値が小さいほど精度が高いことを示しています。

figure
histogram(err)
xlabel("RMSE")
ylabel("Frequency")

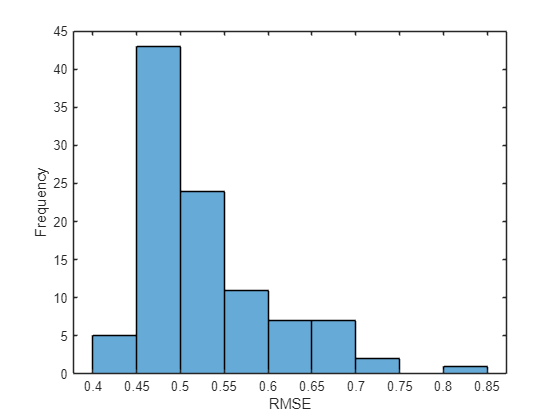
すべてのテスト観測について平均 RMSE を計算します。

mean(err,"all")

ans = single
    0.5304

将来のタイムステップの予測

入力された時系列またはシーケンスについて、将来の複数のタイムステップの値を予測するには、関数 predict を使用して、タイムステップを 1 つずつ予測し、予測ごとに RNN の状態を更新します。予測ごとに、前の予測を関数への入力として使用します。

テストシーケンスの 1 つをプロットに可視化します。

idx = 3;
X = XTest{idx};
T = TTest{idx};

figure
stackedplot(X,DisplayLabels="Channel " + (1:numChannels))
xlabel("Time Step")
title("Test Observation " + idx)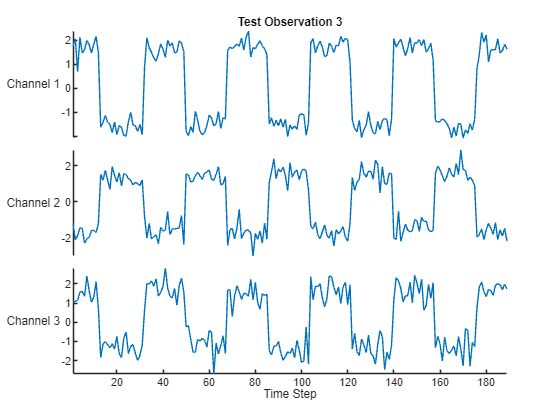

予測には、開ループ予測と閉ループ予測の 2 つの方法があります。

開ループ予測 — 入力データのみを使用してシーケンスの次のタイムステップを予測します。後続のタイムステップの予測を行うときは、真の値をデータソースから収集し、それを入力として使用します。たとえば、1 ～ $t - 1$ のタイムステップで収集されたデータを使用して、そのシーケンスのタイムステップ $t$ の値を予測するとします。タイムステップ $t + 1$ の予測を行うには、タイムステップ $t$ の真の値が記録されるまで待ち、それを入力として使用して次の予測を行います。次の予測を行う前に RNN に提供する真の値がある場合は、開ループ予測を使用します。
閉ループ予測 — 前の予測を入力として使用して、シーケンスの後続のタイムステップを予測します。この場合、モデルは予測を行うために真の値を必要としません。たとえば、1 ～ $t - 1$ のタイムステップでのみ収集されたデータを使用して、シーケンスのタイムステップ $t$ ～ $t + k$ の値を予測するとします。タイムステップ $i$ の予測を行うには、タイムステップ $i - 1$ の予測値を入力として使用します。複数の後続のタイムステップを予測する場合、または次の予測を行う前に RNN に提供する真の値がない場合には、閉ループ予測を使用します。

開ループ予測

開ループ予測を実行します。

まず、関数 resetState を使用して状態をリセットし、RNN の状態を初期化します。次に、入力データの最初のいくつかのタイムステップを使用して初期予測を求めます。入力データの最初の 75 タイムステップを使用して、RNN の状態を更新します。

net = resetState(net);
offset = 75;
[Z,state] = predict(net,X(1:offset,:));
net.State = state;

さらに予測を続行するには、タイムステップ全体にわたってループ処理し、関数 predict を使用して予測を行います。各予測の後、RNN の状態を更新します。入力データをタイムステップ全体にわたってループ処理し、それらを RNN への入力として使用することにより、テスト観測の残りのタイムステップの値を予測します。初期予測の最後のタイムステップが最初の予測タイムステップになります。

numTimeSteps = size(X,1);
numPredictionTimeSteps = numTimeSteps - offset;
Y = zeros(numPredictionTimeSteps,numChannels);
Y(1,:) = Z(end,:);

for t = 1:numPredictionTimeSteps-1
    Xt = X(offset+t,:);
    [Y(t+1,:),state] = predict(net,Xt);
    net.State = state;
end

予測を入力値と比較します。

figure
t = tiledlayout(numChannels,1);
title(t,"Open Loop Forecasting")

for i = 1:numChannels
    nexttile
    plot(X(:,i))
    hold on
    plot(offset:numTimeSteps,[X(offset,i) Y(:,i)'],"--")
    ylabel("Channel " + i)
end

xlabel("Time Step")
nexttile(1)
legend(["Input" "Forecasted"])

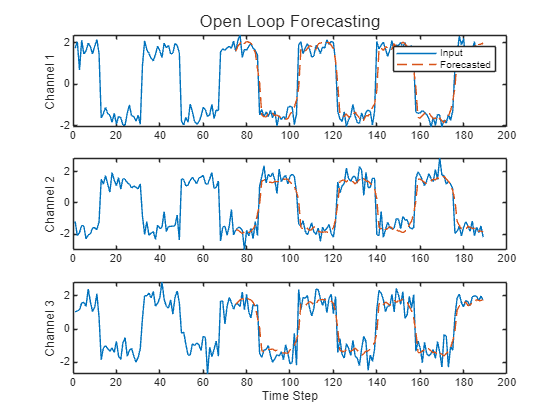
閉ループ予測

閉ループ予測を実行します。

まず、関数 resetState を使用して状態をリセットし、RNN の状態を初期化します。次に、入力データの最初のいくつかのタイムステップを使用して初期予測 Z を求めます。入力データのすべてのタイムステップを使用して、RNN の状態を更新します。

net = resetState(net);
offset = size(X,1);
[Z,state] = predict(net,X(1:offset,:));
net.State = state;

さらに予測を続行するには、タイムステップ全体にわたってループ処理し、関数 predict を使用して予測を行います。各予測の後、RNN の状態を更新します。RNN に前の予測値を繰り返し渡すことにより、次の 200 タイムステップを予測します。RNN はさらに予測を行うための入力データを必要としないため、予測するタイムステップには任意の数を指定できます。初期予測の最後のタイムステップが最初の予測タイムステップになります。

numPredictionTimeSteps = 200;
Y = zeros(numPredictionTimeSteps,numChannels);
Y(1,:) = Z(end,:);

for t = 2:numPredictionTimeSteps
    [Y(t,:),state] = predict(net,Y(t-1,:));
    net.State = state;
end

予測値をプロットに可視化します。

numTimeSteps = offset + numPredictionTimeSteps;

figure
t = tiledlayout(numChannels,1);
title(t,"Closed Loop Forecasting")

for i = 1:numChannels
    nexttile
    plot(X(1:offset,i))
    hold on
    plot(offset:numTimeSteps,[X(offset,i) Y(:,i)'],"--")
    ylabel("Channel " + i)
end

xlabel("Time Step")
nexttile(1)
legend(["Input" "Forecasted"])