敵対的学習デノイザー モデルを使用した信号のノイズ除去
この例では、敵対的学習デノイザー モデル [1] を使用して、ノイズを含む信号のノイズを除去する方法を示します。モデルは、現実の 1 次元信号から成る任意のデータ セットを使用して学習可能なオブジェクトとしてラップされます。学習後、オブジェクトは学習セット内の信号と同様の特性をもつテスト信号をノイズ除去できるようになります。この例では、ノイズを含む心電図 (ECG) 信号と脳波 (EEG) 信号に対するモデルの有効性を示します。これらのタイプの信号は非定常であり、ノイズ スペクトルとオーバーラップする関心スペクトル成分をもっているため、ノイズ除去は困難な問題となります。この例では、敵対的学習モデルを使用して信号のノイズを除去した後、その結果を従来のウェーブレット ノイズ除去手法および LSTM ネットワーク デノイザー モデルの結果と比較します。
敵対的学習デノイザー モデル
敵対的学習と敵対的生成ネットワーク (GAN) はイメージ生成で広く使用されてきましたが、現在では信号処理を含む他の分野にも適用されています。敵対的モデルには、ディスクリミネーターを騙そうとするデータを生成するジェネレーターと、人工的に生成されたデータと現実のデータを区別するディスクリミネーターという 2 つの主要なコンポーネントが含まれます。
この例では、クリーンな信号とノイズを含む信号を使用して敵対的学習モデルに学習させます。モデルは信号デノイザーとして機能し、次のような学習アーキテクチャをもっています。

学習入力データは、クリーンな実現とノイズを含む実現の両方を含む信号セットで構成されます。"符号化器" はジェネレーターでもあり、入力信号の符号化潜在表現を生成します。符号化表現が次の 2 つの要件を満たしていることが理想的です。
表現は、ノイズ情報を符号化しておらず、クリーンな入力信号から符号化されたとディスクリミネーターを騙すのに十分なほどクリーンである。
表現は、復号化器が元の信号を再構成するのに十分な情報を符号化している。
ディスクリミネーターは、潜在表現がクリーンな入力信号から生成されたものか、ノイズを含む入力信号から生成されたものかを識別する役割を担います。最後に、復号化器は潜在表現からノイズ除去した信号を再構成します。ディスクリミネーターと復号化器は両方とも、計算された損失値の形式でフィードバックを提供します。システムはこのフィードバックを使用して、符号化器、ディスクリミネーター、および復号化器を更新します。
"Loss1" は、生成されたノイズ除去信号とクリーンな入力信号の間の平均二乗誤差 (MSE) です。"Loss2"、"Loss3"、および "Loss4" はすべて、ディスクリミネーターからの予測ラベルのクロスエントロピー損失です。モデルは、ノイズを含むソース信号学習セットを使用して "Loss2" と "Loss4" を計算し、クリーンなソース信号学習セットを使用して "Loss3" を計算します。
"Loss4" のターゲット ラベルは、符号化器がディスクリミネーターを騙そうとするために常にノイズを含む信号入力を使用して計算されているにもかかわらず、クリーンです。
データの準備
この例では、Physionet ECG-ID データベース [2] [3] を使用します。このデータベースには、90 人の被験者からの 310 個の ECG 記録が含まれています。各記録には、ノイズを含む生の ECG 信号と、手動でフィルター処理されたクリーンなグラウンド トゥルース バージョンが含まれています。
データ セットをローカル フォルダーに保存するか、次のコードを使用してデータをダウンロードします。
datasetFolder = fullfile(tempdir,"ecg-id-database-1.0.0"); if ~isfolder(datasetFolder) loc = websave(tempdir,"https://physionet.org/static/published-projects/ecgiddb/ecg-id-database-1.0.0.zip"); unzip(loc,tempdir); end
データを管理するためのsignalDatastore (Signal Processing Toolbox)オブジェクトを作成します。10 人の異なる被験者からのデータをテスト セットとしてランダムに選択します。乱数シードをリセットして、データ セグメンテーションと可視化の結果が再現可能になるようにします。
sds = signalDatastore(datasetFolder, ... IncludeSubfolders = true, ... FileExtensions = ".dat", ... ReadFcn = @helperReadSignalData); rng("default") subjectIds = unique(extract(sds.Files,"Person_"+digitsPattern)); testSubjects = contains(sds.Files,subjectIds(randperm(numel(subjectIds),10))); testDs = subset(sds,testSubjects);
残りのデータの 80% を学習に使用し、20% を検証に使用します。
trainAndValDs = subset(sds,~testSubjects); trainAndValDs = shuffle(trainAndValDs); [trainInd,valInd] = dividerand(1:numel(trainAndValDs.Files),0.8,0.2,0); trainDs = subset(trainAndValDs,trainInd); validDs = subset(trainAndValDs,valInd);
敵対的信号デノイザー オブジェクトの学習
後で学習とノイズ除去に使用するために、信号デノイザー オブジェクトを作成します。モデルは信号長に依存するため、オブジェクトは固定長の信号でのみ機能します。モデル作成時に信号長を指定します。
sampleSignal = preview(trainDs);
signalLength = length(sampleSignal{1});
advDenoiser = helperAdversarialSignalDenoiser(signalLength);関数 train を使用して、デノイザー オブジェクトに学習させます。追加のオプションの引数入力を渡して学習プロセスをカスタマイズすることで、複数の学習オプションを指定できます。
学習プロセスをスキップして、事前学習済みのオブジェクトを直接読み込む場合は、doTrain フラグを false に設定します。
doTrain =true; if doTrain train(advDenoiser,trainDs,... ValidationData = validDs, ... MaxEpochs = 100, ... MiniBatchSize = 32, ... Plots = true, ... Normalization = true); else zipFile = matlab.internal.examples.downloadSupportFile('SPT','data/adversarialLearningDenoiserModelParameters.zip'); unzip(zipFile); loadParameters(advDenoiser,"adversarialLearningDenoiserModelParameters"); end
Training loss after epoch 1: 1.7162 Training loss after epoch 10: 0.011477 Training loss after epoch 20: 0.018192 Training loss after epoch 30: 0.0096357 Training loss after epoch 40: 0.044912 Training loss after epoch 50: 0.003166 Training loss after epoch 60: 0.060249 Training loss after epoch 70: 0.0038481 Training loss after epoch 80: 0.0061918 Training loss after epoch 90: 0.0021122 Training loss after epoch 100: 0.001513

テスト データ セットの信号のノイズ除去
denoise を使用し、テスト信号データストア testDs 内の信号データでデノイザー オブジェクトをテストします。関数 denoise が使用するバッチ サイズと実行環境を指定できます。関数 denoise の出力もデータストアであることに注意してください。
denoisedSignalsDs = denoise(advDenoiser,testDs, ... "MiniBatchSize",32, ... "ExecutionEnvironment","auto");
データストアからクリーンな信号、ノイズを含む信号、およびノイズ除去された信号を取得し、行方向の行列として保存します。
testData = readall(testDs);
denoisedSignals = readall(denoisedSignalsDs);
denoisedSignals = cat(1,denoisedSignals{:});
noisySignals = cellfun(@(x) x(1),testData);
noisySignals = cat(1,noisySignals{:});
cleanSignals = cellfun(@(x) x(2),testData);
cleanSignals = cat(1,cleanSignals{:});元の S/N 比 (SNR) 値とノイズ除去後の S/N 比 (SNR) 値を比較します。
N = size(cleanSignals,1); snrsNoisy = zeros(N,1); snrsDenoised = zeros(N,1); snrsWaveletDenoised = zeros(N,1); for i = 1:N snrsNoisy(i) = snr(cleanSignals(i,:),cleanSignals(i,:)-noisySignals(i,:)); end for i = 1:N snrsDenoised(i) = snr(cleanSignals(i,:),cleanSignals(i,:)-denoisedSignals(i,:)); end SNRs = [snrsNoisy,snrsDenoised]; bins = -10:2:16; count = zeros(2,length(bins)-1); for i =1:2 count(i,:) = histcounts(SNRs(:,i),bins); end bar(bins(1:end-1),count,"stack"); legend(["Noisy","Denoised (advDenoiser)"],"Location","northwest") title("SNR of the Noisy and Denoised Signals") xlabel("SNR (dB)") ylabel("Number of Samples") grid on

ノイズ除去後の最良の SNR 値と最悪の SNR 値を表示し、対応する信号をプロットします。元のノイズを含む一部の信号は非常に歪んでいますが、どちらの場合でもノイズ削減効果は依然として明瞭です。
[bestSNR,bestSNRIdx] = max(snrsDenoised)
bestSNR = 14.2563
bestSNRIdx = 9
[worstSNR,worstSNRIdx] = min(snrsDenoised)
worstSNR = -1.8763
worstSNRIdx = 19
helperPlotDenoisedSignal(bestSNRIdx,worstSNRIdx,noisySignals,denoisedSignals,cleanSignals)


ウェーブレット ノイズ除去との結果の比較
深層学習アプローチを使用して信号処理の問題を解決するときに生じる一般的な疑問は、それらの手法が古典的な、または従来の信号処理手法とどのように比較されるかということです。敵対的学習モデルの性能を従来のウェーブレット ノイズ除去手法と比較します。ウェーブレット ノイズ除去関数wdenoise (Wavelet Toolbox)を使用して、テスト信号のノイズを除去します。この例のパラメーターは、元の論文 [1] の著者が網羅的探索を行って取得したものです。
noisySignalsNormalized = noisySignals - mean(noisySignals,2); waveletDenoisedSignals = wdenoise(double(noisySignalsNormalized),... Wavele = "sym8", ... ThresholdRule = "soft", ... NoiseEstimate = "LevelDependent");
ウェーブレット ノイズ除去信号の SNR を計算して可視化します。
for i = 1:N snrsWaveletDenoised(i) = snr(cleanSignals(i,:),cleanSignals(i,:)-waveletDenoisedSignals(i,:)); end SNRs = [snrsNoisy,snrsDenoised snrsWaveletDenoised]; bins = -10:2:16; count = zeros(3,length(bins)-1); for i =1:3 count(i,:) = histcounts(SNRs(:,i),bins); end bar(bins(1:end-1),count,"stack"); legend(["Noisy","Denoised (advDenoiser)","Denoised (wavDenoiser)"],"Location","best") title("SNR of the Noisy and Denoised Signals") xlabel("SNR (dB)") ylabel("Number of Samples") grid on

最悪の SNR と最良の SNR について、ウェーブレット ノイズ除去信号と敵対的ノイズ除去信号をプロットします。
helperPlotDenoisedSignal(bestSNRIdx,worstSNRIdx,noisySignals,denoisedSignals,cleanSignals,waveletDenoisedSignals)
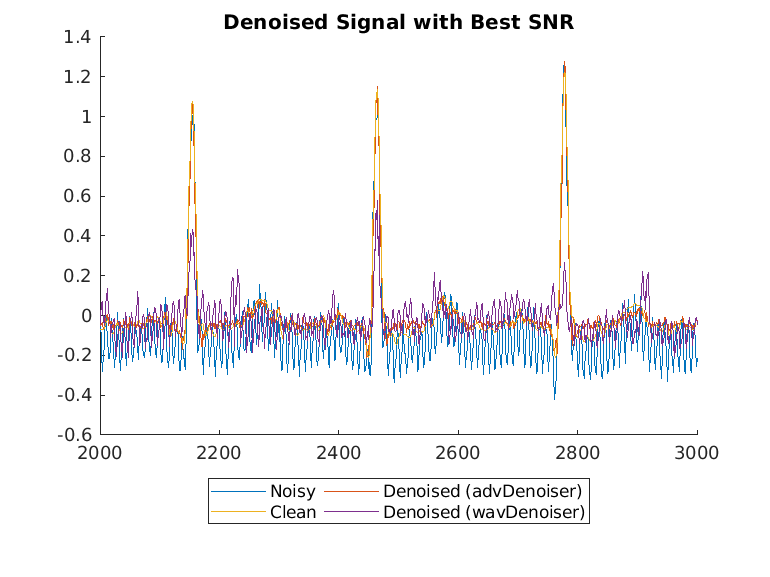

敵対的デノイザーは、特に最悪の SNR 値に対して、ウェーブレット デノイザーよりも優れたパフォーマンスを発揮します。
このデータ セットのグラウンド トゥルースとして使用されるクリーンな信号は、信号とノイズに関する事前の知識に基づいて、いくつかの従来のノイズ削減方法を組み合わせて手動でフィルター処理されていることに注意してください。これらの従来の方法も信号のノイズを除去するのにうまく機能しますが、この例の敵対的ノイズ除去モデルは信号のノイズ除去を適用するための予備知識を必要としません。
異なるデータ セットに対するデノイザー オブジェクトの適用
他の多くのデータ セットを使用して、敵対的学習信号デノイザー オブジェクトに学習させることができます。たとえば、デノイザーを使用して EEG 信号のノイズを除去できます。
敵対的信号デノイザーの性能を理解するために、このモデルを、短時間フーリエ変換 (STFT) 機能を入力として使用する LSTM ネットワーク stftNet と比較しました。敵対的デノイザー オブジェクトと stftNet を、異なる SNR の EOG 信号によって汚染された EEG 信号をノイズ除去するために使用しました。stftNet と EEG データ セットの詳細については、Denoise EEG Signals Using Differentiable Signal Processing Layers (Signal Processing Toolbox)を参照してください。
敵対的デノイザー オブジェクトと stftNet には、EEG 信号の元のセットの 10% を使用して学習させました。プロットは、2 つのモデルの性能を平均二乗誤差で示したものです。プロットには比較のために、ノイズ除去していない、ノイズを含む元の信号の平均二乗誤差も示しています。
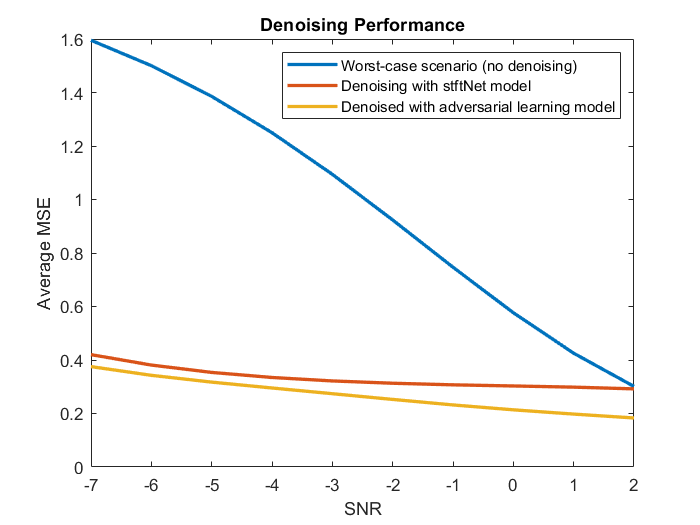
特に SNR が大きい場合、敵対的モデルは stftNet モデルよりも優れた性能を発揮します。
参考文献
[1] Casas, Leslie, Attila Klimmek, Nassir Navab, and Vasileios Belagiannis. “Adversarial Signal Denoising with Encoder-Decoder Networks.” In 2020 28th European Signal Processing Conference (EUSIPCO), 1467–71. Amsterdam, Netherlands: IEEE, 2021. https://doi.org/10.23919/Eusipco47968.2020.9287738.
[2] Lugovaya, Tatiana. 2005."Biometric Human Identification Based on Electrocardiogram." Master's thesis, Saint Petersburg Electrotechnical University.
[3] Goldberger, Ary L., Luis A. N. Amaral, Leon Glass, Jeffrey M. Hausdorff, Plamen Ch. Ivanov, Roger G. Mark, Joseph E. Mietus, George B. Moody, Chung-Kang Peng, and H. Eugene Stanley. “PhysioBank, PhysioToolkit, and PhysioNet.” Circulation 101, no. 23 (June 13, 2000): e215–20. https://doi.org/10.1161/01.CIR.101.23.e215.
[4] Zhang, Haoming, Mingqi Zhao, Chen Wei, Dante Mantini, Zherui Li, and Quanying Liu. “EEGdenoiseNet: A Benchmark Dataset for End-to-End Deep Learning Solutions of EEG Denoising.” Preprint, submitted July 28, 2021. https://arxiv.org/abs/2009.11662.
付録: 補助関数
function [dataOut,infoOut] = helperReadSignalData(filename) fid = fopen(filename,"r"); % 1st row : raw data, 2nd row : filtered data data = fread(fid,[2 Inf],"int16=>single"); fclose(fid); fid = fopen(replace(filename,".dat",".hea"),"r"); header = textscan(fid,"%s%d%d%d",2,"Delimiter"," "); fclose(fid); gain = single(header{3}(2)); dataOut{1} = data(1,:)/gain; % noisy, raw data dataOut{2} = data(2,:)/gain; % filtered, clean data infoOut.SampleRate = header{3}(1); end function helperPlotDenoisedSignal(varargin) bestSNRidx = varargin{1}; worstSNRidx = varargin{2}; plotRange = 2000:3000; labels = ["Noisy","Denoised (advDenoiser)","Clean","Denoised (wavDenoiser)"]; figure hold on for i = 3:nargin signal = varargin{i}; plot(plotRange,(signal(bestSNRidx,plotRange))); end legend(labels(1:nargin-2),Location="southoutside",Orientation = "horizontal",NumColumns=2) title("Denoised Signal with Best SNR") hold off figure hold on for i = 3:nargin signal = varargin{i}; plot(plotRange,(signal(worstSNRidx,plotRange))); end legend(labels(1:nargin-2),Location="southoutside",Orientation = "horizontal",NumColumns=2) title("Denoised Signal with Worst SNR") hold off end
PhysioNet ECG-ID データベースからの情報が含まれます。このデータベースは、ODC Attribution License (https://opendatacommons.org/licenses/by/1-0/ で参照可能) に基づいて利用可能です。
参考
関数
wdenoise(Wavelet Toolbox)
オブジェクト
signalDatastore(Signal Processing Toolbox)