このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

多出力の誤差の正規化

ニューラル ネットワークの学習に使用される最も一般的な性能関数は、平均二乗誤差 (mse) です。ただし、値の範囲が異なる複数の出力がある場合、平均二乗誤差を使用する学習では、値の範囲が狭い出力要素に比べ、値の範囲が広い出力要素に基づいて精度を最適化する傾向があります。

たとえば、次の 2 つのターゲット要素の範囲は大きく異なります。

x = -1:0.01:1;
t1 = 100*sin(x);
t2 = 0.01*cos(x);
t = [t1; t2];

t1 の範囲は 200 (最小 -100 から最大 100 まで) ですが、t2 の範囲はわずか 0.02 (-0.01 から 0.01 まで) です。t1 の範囲は、t2 の範囲の 10,000 倍の大きさです。

この条件でニューラル ネットワークを作成して学習させ、平均二乗誤差を最小化した場合、学習は 2 番目の出力要素よりも最初の出力要素の相対精度に偏ります。

net = feedforwardnet(5);
net1 = train(net,x,t);

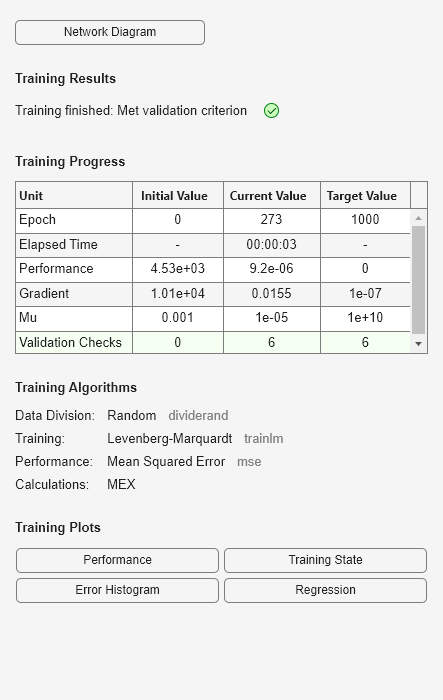
y = net1(x);

ここでは、ネットワークが、最初の出力要素が非常によく当てはまるような学習をしていることがわかります。

figure(1)
plot(x,y(1,:),x,t(1,:))

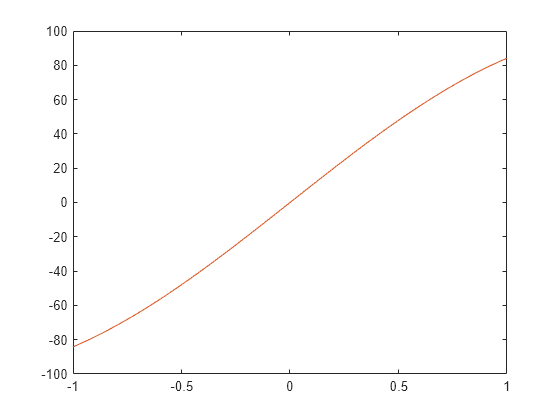
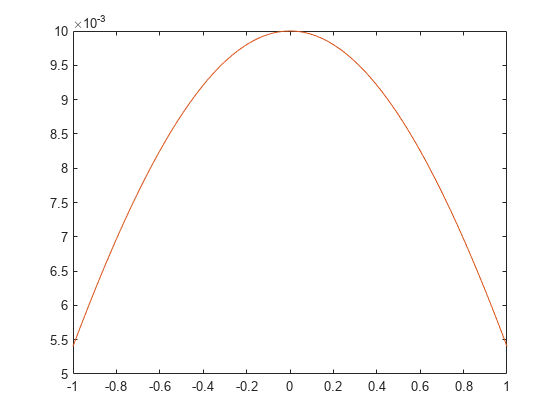
一方で、2 番目の要素の関数は、あまり適切に当てはまっていません。

figure(2)
plot(x,y(2,:),x,t(2,:))

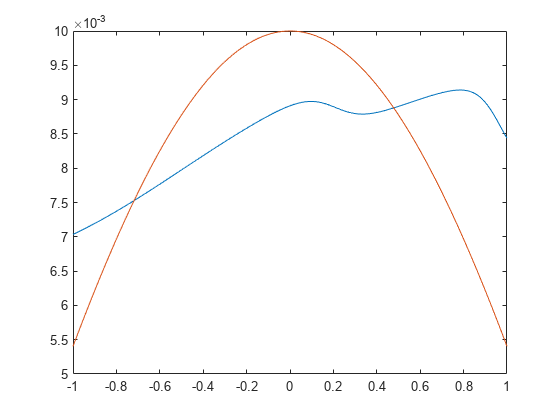
両方の出力要素について相対的に同等に適合させるためには、normalization 性能パラメーターを 'standard' に設定します。この場合、性能測定の誤差は、各出力要素の範囲を 2 として (つまり、各出力要素の値の範囲が異なる範囲ではなく、-1 から 1 であるとして) 計算されます。

net.performParam.normalization = 'standard';
net2 = train(net,x,t);

y = net2(x);

これで、2 つの出力要素がどちらも適切に当てはまります。

figure(3)
plot(x,y(1,:),x,t(1,:))

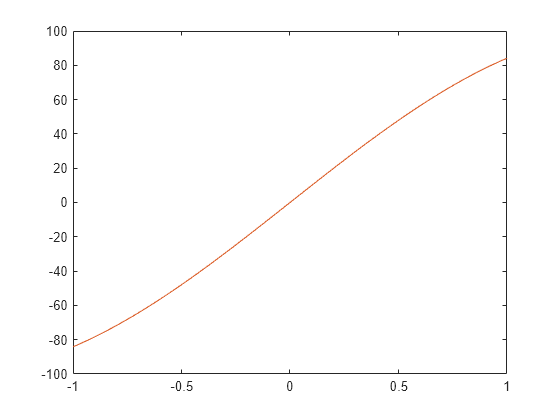
figure(4)
plot(x,y(2,:),x,t(2,:))