ニューロン モデル
シンプルなニューロン
ニューラル ネットワークの基本構成は、この例のような単入力ニューロンです。
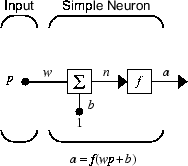
この例のニューロンで実行されるのは、異なる 3 つの関数演算です。最初に、スカラー入力 p にスカラーの重み w が乗算され、同じくスカラーである積 wp になります。次に、重み付けされた入力 wp にスカラーのバイアス b が加算され、正味入力 n になります (この場合、バイアスは関数 f の b 分の左シフトと見なせます。バイアスは、定数入力 1 をもつ点を除いて、重みとよく似ています)。最後に、正味入力が伝達関数 f に渡され、スカラー出力 a が生成されます。これら 3 つの処理には、重み関数、正味入力関数、および伝達関数という名前が付いています。
多くのタイプのニューラル ネットワークでは、重み関数は重みと入力の積ですが、場合によっては、他の重み関数 (重みと入力の距離 |w - p| など) も使用されます (重み関数の一覧については、help nnweight と入力してください)。最も一般的な正味入力関数は、重み付けされた入力とバイアスの和ですが、乗算など他の演算も使用できます (正味入力関数の一覧については、help nnnetinput と入力してください)。放射基底ニューラル ネットワークの概要では、距離を重み関数として使用し、乗算を正味入力関数として使用する方法を説明しています。伝達関数にも数多くのタイプがあります。さまざまな伝達関数の例が、伝達関数に記載されています (伝達関数の一覧については、help nntransfer と入力してください)。
w と b はどちらも、ニューロンの "調整可能な" スカラー パラメーターであることに注意してください。ニューラル ネットワークの中心となる考え方は、ネットワークが目的のまたは関心対象となる動作を示すように、これらのパラメーターを調整できるということです。したがって、重みまたはバイアス パラメーターを調整することで、ネットワークに特定のジョブの実行を学習させることができます。
Deep Learning Toolbox™ ソフトウェアのすべてのニューロンはバイアスへの用意があります。バイアスは例の多くで使用されており、このツールボックスのほとんどでバイアスが想定されています。ただし、必要に応じて、ニューロンのバイアスを省略できます。
伝達関数
多数の伝達関数が Deep Learning Toolbox ソフトウェアに含まれています。
最もよく使用される 2 つの関数を以下に示します。
次の図は線形伝達関数を示しています。
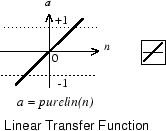
このタイプのニューロンは、関数近似を目的とした多層ネットワークの最後の層で使用されます。これについては、浅層の多層ニューラル ネットワークと逆伝播学習に示します。
以下に示すシグモイド伝達関数は、負の無限大から正の無限大の間にある任意の値を入力として取り、出力を 0 から 1 の範囲にスカッシングします。
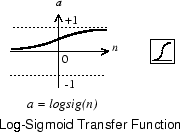
この伝達関数は多層ネットワークの隠れ層で一般的に使用されますが、これは 1 つには、この関数が微分可能であるためです。
上に示した各伝達関数のグラフの右にある正方形内の記号は、対応する伝達関数を表します。これらのアイコンは、ネットワーク図のブロック内の通常の f に代わり、使用されている特定の伝達関数を示します。
伝達関数の詳細な一覧については、help nntransfer と入力してください。また、独自の伝達関数を指定することもできます。
ベクトル入力を持つニューロン
シンプルなニューロンは、ベクトル入力を扱うように拡張できます。以下に、単一の R 要素入力ベクトルを持つニューロンを示します。ここで、個々の入力要素
に次の重みが乗算され
重み付けされた値がサミング ジャンクションに渡されます。これらの和は単に、(単一行の) 行列 W とベクトル p のドット積 Wp です (ドット積だけでなく、放射基底ニューラル ネットワークの概要にあるように、重み行列の行と入力ベクトルの間の距離など、他の重み関数もあります)。
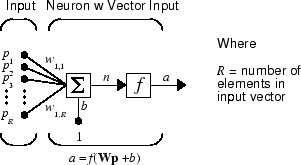
このニューロンにはバイアス b があり、重み付けされた入力に加算され、正味入力 n になります (加算だけでなく、放射基底ニューラル ネットワークの概要で使用されている乗算など、他の正味入力関数も使用できます)。正味入力 n は伝達関数 f の引数です。
もちろん、この式は、MATLAB® コードで次のように記述できます。
n = W*p + b
ただし、このようなコードは、ネットワーク全体を定義しシミュレーションを行う関数に既に組み込まれているため、このレベルのコードを書くことはほとんどありません。
省略表記
上に示した 1 つのニューロンの図には、詳細が多数含まれています。多数のニューロン、そしておそらくは多数のニューロンから成る層を含むネットワークを考える場合、詳細が多くなりすぎて、主要な概念が見落とされる傾向があります。そのため、個々のニューロンの省略表記が考案されています。この表記を以下に示します。この表記は、以降の複数のニューロンから成る回路で使用されます。
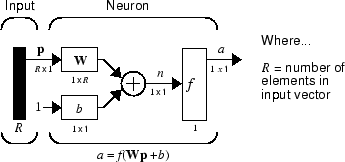
ここで、入力ベクトル p は、左側の黒い垂直バーで表現されます。p の次元は、図の記号 p の下に R × 1 と表示されています (なお、前文の R のような大文字は、ベクトルの "サイズ" を参照するときに使用されます)。したがって、p は R 個の入力要素のベクトルです。これらの入力には、1 行 R 列の行列 W が右から乗算されます。前と同じように、定数 1 が入力としてニューロンに渡され、スカラー バイアス b が乗算されます。伝達関数 f への正味入力は n、つまり、バイアス b と積 Wp の和です。この和が伝達関数 f に渡され、ニューロンの出力 a が得られます。この場合、出力はスカラーです。ニューロンが複数ある場合、ネットワークの出力はベクトルになることに注意してください。
前の図では、1 つの "層" のネットワークが定義されています。1 つの層には、重み、乗算および加算 (ここでは、ベクトルの積 Wp に対応)、バイアス b、および伝達関数 f が含まれています。入力の配列であるベクトル p は、層には含まれず、層とは呼ばれません。
シンプルなニューロンと同様に、層にはそこで実行される 3 つの演算、重み関数 (この場合は行列の乗算、つまりドット積)、正味入力関数 (この場合は加算)、および伝達関数があります。
このネットワークの省略表記を使用するときは、行列のサイズが行列変数名のすぐ下にいつも表示されます。この表記により、アーキテクチャを理解して、アーキテクチャに関連する行列演算処理を把握できます。
伝達関数で説明されているように、特定の伝達関数が図で使用される場合、その伝達関数の記号が上記の f に代わります。こちらはその例です。
