深層学習を使用したバッテリー サイクル寿命の予測
物理学に基づいたモデル化手法を使用したリチウムイオン バッテリーのサイクル寿命の予測は、動作状態が多岐にわたり、製造元が同じバッテリーでもデバイスの変動性が大きいため、非常に複雑です。また、バッテリーは使用状況や製造時の状態により、それぞれ経年劣化の仕方が異なります。この例では、深層学習技術を使用して、急速充電されたリチウムイオン バッテリーの残量サイクルを推定する方法について説明します。バッテリーのライフサイクルを表すデータを使用して 2 次元畳み込みニューラル ネットワーク ベースのアーキテクチャに学習させ、この学習済みネットワークを使用して、新しいバッテリーの残りのサイクル寿命を推定します。
データ セット
データ セットには、定格容量 1.1 Ah、定格電圧 3.3 V のリチウムイオン電池 40 個から取られた、さまざまな充放電プロファイルにおける測定値が格納されています。各バッテリーは、あらかじめ決められたポリシーに従って、電池容量の 80% に達するまで充電と放電を繰り返します。この状態になるまでのサイクル数をバッテリー サイクル寿命といいます。この数値は、この例で使用しているデータのヒストグラムに見られるように、150 ~ 2300 サイクルの間で大きく変化します。
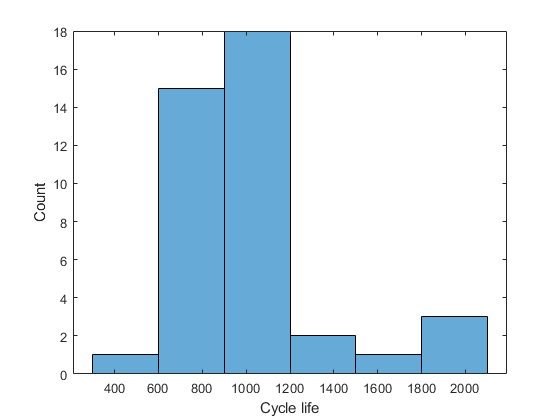
124 個の電池の測定値を含むデータ セット全体にはこちら [2] から、詳細説明にはこちら [1] からアクセスできます。この例では、ダウンロードと実行をしやすくするため、40 個の電池の測定値のみを含むデータ量を減らしたデータ セットを使用しています。各バッテリーのデータは構造体に格納され、次の情報が含まれています。
サイクル内で収集されるデータ: 電流、電圧、温度、容量、差動放電容量
MathWorks® サポート ファイル サイトからデータを読み込みます (これは約 1.2 GB の大きなデータ セットです)。
url = 'https://ssd.mathworks.com/supportfiles/predmaint/batterycyclelifeprediction/v2/batteryDischargeData.zip'; websave('batteryDischargeData.zip',url); unzip('batteryDischargeData.zip') load('batteryDischargeData');
データ中の最初のバッテリーの 1 フル サイクルの電流、電圧、温度測定値のプロットを作成し、データ特性を可視化します。
battIndx = 1; cycleIndx = 1; batteryMeasurements = table(batteryDischargeData(battIndx).cycles(cycleIndx).I,batteryDischargeData(battIndx).cycles(cycleIndx).V,... batteryDischargeData(battIndx).cycles(cycleIndx).T, batteryDischargeData(battIndx).cycles(cycleIndx).Qd); stackedplot(batteryMeasurements, "Title","Measurements over one cycle",... "DisplayLabels", ["Current (A)","Voltage(V)","Temperature(C)","DischargeCapacity(Ah)"], ... "Xlabel", "Sample Index");
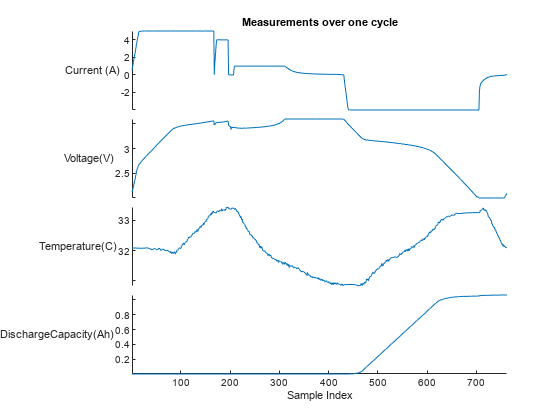
先ほどのプロットでは、正の電流は充電動作を、負の電流は放電動作を表しています。バッテリーが 3.6 V になると満充電、2 V になると完全放電の状態です。さらに、このデータ セットでは、バッテリーの劣化プロファイルを時間や負荷に応じて理解するために、さまざまな急速充電ポリシーが適用されています。
バッテリー放電測定値の抽出
バッテリーの充電ポリシーはすべて異なりますが、放電電圧範囲は同じであるため、この例では信号の放電部分のみを使用します。補助関数 hExtractDischargeData を使用して、サイクルの放電部分に対応する測定値を抽出します。1 個目のバッテリーの最初のサイクルの放電データをプロットします。
dischargeData = hExtractDischargeData(batteryDischargeData);
batteryMeasurements = table(dischargeData{battIndx}.Vd{cycleIndx},dischargeData{battIndx}.Td{cycleIndx},...
dischargeData{battIndx}.QdClipped{cycleIndx});
stackedplot(batteryMeasurements, "Title","Measurements over one cycle",...
"DisplayLabels", ["Voltage(V)","Temperature(C)","DischargeCapacity(Ah)"],...
"Xlabel", "Sample Index");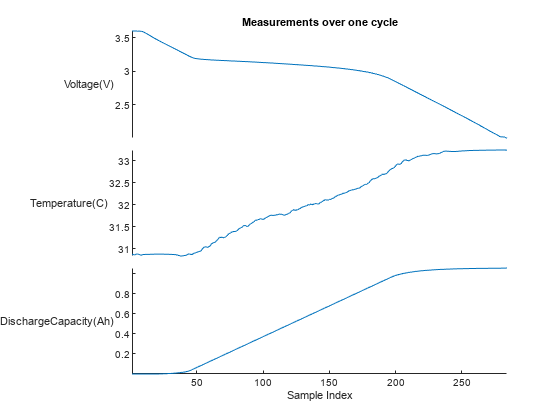
このデータ セットのバッテリーはさまざまな充電ポリシーでテストされているため、サイクルによっては他のサイクルよりも先に完了します。したがって、サイクル時間はバッテリー間の充電と温度の比較には使用できません。放電時間は接続された負荷やバッテリーの健全性によって変化するため、時間の代わりに電圧範囲を基準としています。また、電荷と温度の測定値は、この電圧範囲にわたって内挿されます。関数 hLinearInterpolation を使用して、電圧、温度、および放電容量の測定値を、3.6 V ~ 2 V の均一にサンプリングされた 900 個の点の電圧範囲に内挿します。内挿されたデータは、測定値ごとに 30 行 30 列の配列として返され、バッテリーの放電サイクルごとに 2 次元表現が形成されます。900x1 ベクトルを 30x30 行列に形状変更すると、畳み込みネットワークが行列の各列間の空間関係を検索することに注意してください。この例では、そのような関係がさまざまなサイクルにわたって存在する可能性があると想定し、存在する場合はそれを活用します。下のイメージは、900 個の点に内挿されてから 30 行 30 列に形状変更された電池の 1 サイクルの温度と電圧のデータを示しています。各サイクルの測定値の 2 次元表現は、センサーの測定値を CNN 層のイメージ形式に変換します。
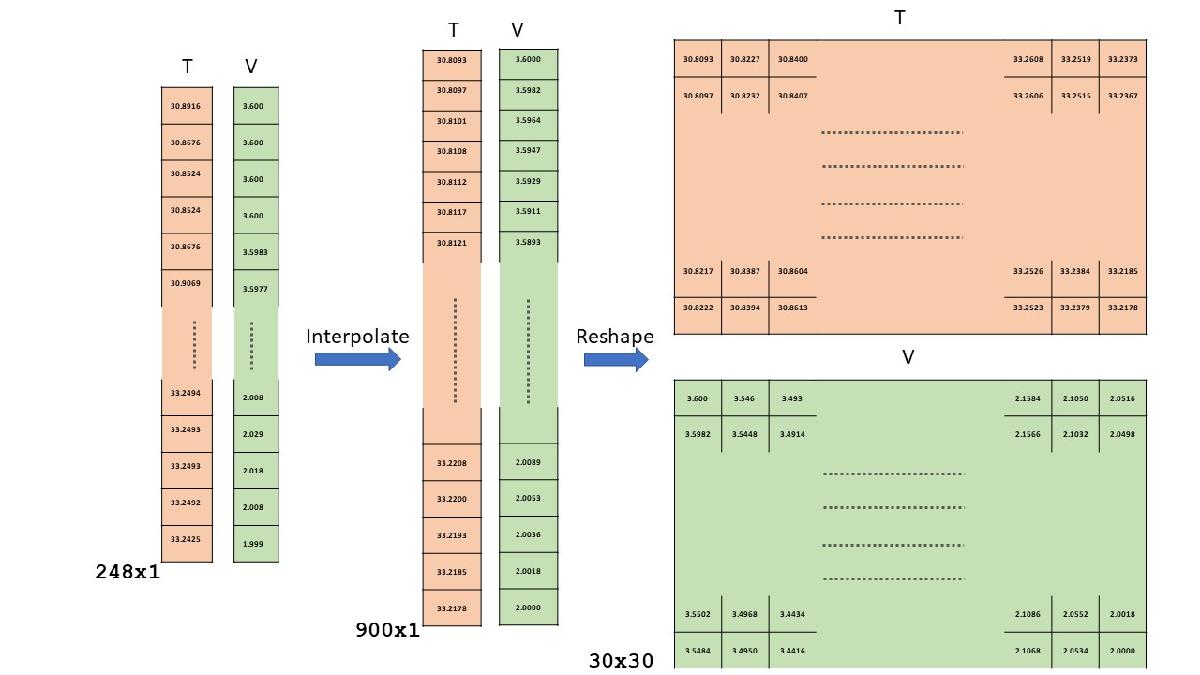
[VInterpol,TInterpol,QdInterpol] = hLinearInterpolation(dischargeData);
内挿温度と放電容量を、電圧の関数としてプロットします。
figure yyaxis left plot(reshape(VInterpol{1}{1}, 900, 1),reshape(TInterpol{1}{1},900,1)) title('Measurements as a function of Voltage') ylabel('Temperature') xlabel('Voltage') yyaxis right plot(reshape(VInterpol{1}{1},900,1),reshape(QdInterpol{1}{1},900,1)) ylabel('Discharge Capacity')
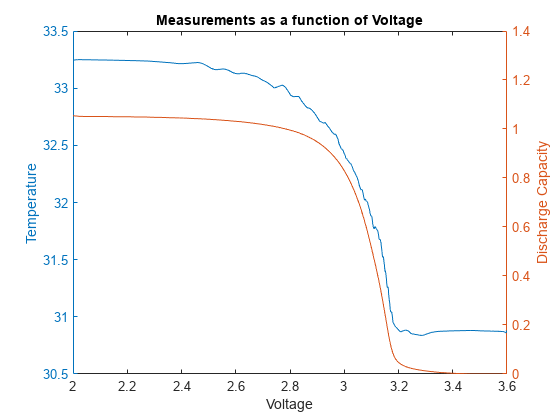
深層ネットワークの 2D 畳み込みニューラル ネットワーク層では、内挿された電圧、放電容量、および温度の 30 行 30 列の行列が、各サイクルの 30x30x3 行列を形成するように形状変更されます。これは、イメージの RGB チャネルに似ています。推定される残りのサイクルの範囲を最小化するには、予測される出力信号を 2000 (データ内のバッテリーの最大寿命) で除算して正規化します。30 個のバッテリーから得られたデータを学習に使用し、5 個のバッテリーを検証に、5 個のバッテリーを深層ニューラル ネットワークのテストに使用します。hreshapeData 補助関数を使用して、各ラベルの 30x30x3 データ セットをすべて作成します。この関数は、測定データ (trainData) と RUL データ (trainRulData) を出力し、各ケースのラベルとして使用します。
testBatteryIndex = 2:8:40; valBatteryIndex = 1:8:40; trainBatteryIndex = setdiff(1:40,[2:8:40 1:8:40]); [trainData,trainRulData] = hreshapeData(VInterpol(trainBatteryIndex), ... TInterpol(trainBatteryIndex),QdInterpol(trainBatteryIndex)); [valData,ValRulData] = hreshapeData(VInterpol(valBatteryIndex), ... TInterpol(valBatteryIndex),QdInterpol(valBatteryIndex)); [testData,testRulData] = hreshapeData(VInterpol(testBatteryIndex), ... TInterpol(testBatteryIndex),QdInterpol(testBatteryIndex)); fprintf('Size of reshaped matrix of interpolated measurement data:%dx%dx%dx%d\n', ... size(trainData))
Size of reshaped matrix of interpolated measurement data:30x30x3x30706
ネットワーク アーキテクチャの定義
畳み込みニューラル ネットワークのアーキテクチャの定義には、層の種類の選択、層の数の選択、テスト データに対して満足な性能が得られるまでのハイパーパラメーターの調整が含まれます。このセクションでは、層の種類と層の数を指定します。深層ニューラル ネットワーク構造を作成するには、連続するネットワーク層のセットを定義します。次の層でネットワーク構造を使用します。
イメージ入力層 — 電圧、放電容量、温度データを入力イメージの 3 つのカラー チャネルとして扱い、測定値を範囲 [0,1] に正規化します。
2 次元畳み込み層 — これらの各層は、スライディング畳み込みフィルターをイメージ入力に適用します。この例では、4 つの隠れ畳み込み層を使用します。試行錯誤によって選択されたこの層の数は、妥当な学習時間を維持しながら最良の結果をもたらします。
レイヤー正規化層 — 各畳み込み層の後にレイヤー正規化層が続きます。これにより、ネットワークの学習が高速化され、ネットワーク初期化に対する感度が低下します。
ReLU 層 — 各レイヤー正規化層の後には、入力の各要素に対してしきい値演算を実行する非線形活性化関数が続きます。
プーリング層 — 最初の 2 つの ReLU 層の後にプーリング層が続き、特徴マップのサイズを小さくします。これらの層は冗長な情報を削除し、後続の層で学習すべきパラメーターの数を減少させます。
全結合層 — 最後に、ReLU 層の後に全結合層が続きます。これは、学習したすべての特徴を単一の出力に結合します。
layers = [ imageInputLayer([30 30 3],"Normalization","rescale-zero-one") convolution2dLayer(3,8,"Padding","same") layerNormalizationLayer reluLayer maxPooling2dLayer(2,"Stride",2) convolution2dLayer(3,16,"Padding","same") layerNormalizationLayer reluLayer averagePooling2dLayer(2,'Stride',2) convolution2dLayer(3,32,'Padding','same') layerNormalizationLayer reluLayer convolution2dLayer(3,32,'Padding','same') layerNormalizationLayer reluLayer convolution2dLayer(3,32,'Padding','same') layerNormalizationLayer reluLayer fullyConnectedLayer(1)]; figure; plot(dlnetwork(layers))

ネットワーク ハイパーパラメーターの定義とネットワークの学習
このセクションでは、前のセクションで指定したネットワークのハイパーパラメーターを定義します。学習率やバッチ サイズなどのハイパーパラメーターの選択は、通常、選択したネットワークとデータ セットに最適なセットを検出してネットワークから満足な性能を得ることを目標に、試行錯誤によって行われます。
この例では、計算時間が短く、調整するパラメーターがほとんどない Adam (適応モーメント推定) オプティマイザーを使用します。ソルバーを次のように構成します。
256 個の観測値のミニバッチ サイズを使用します。
データ セット全体を 50 回学習させます。これは学習エポックの数です。
各エポックの前にデータ セットをシャッフルして収束を改善します。
収束とオーバーシュートのバランスが取れた学習率 0.001 を使用します。
ネットワークを定期的に検証して、ネットワークが学習データを過適合している時期を特定します。
Adam ソルバーの学習オプションの詳細については、TrainingOptionsADAMを参照してください。この例で使用した学習ハイパーパラメーターは、試行錯誤の結果として選択したものです。パラメーターを調整して、学習をさらに改善できます。
miniBatchSize = 256; validationFrequency = 10*floor(numel(trainRulData)/miniBatchSize); options = trainingOptions("adam", ... "MaxEpochs",100, ... "MiniBatchSize",miniBatchSize, ... "Plots","training-progress", ... "Metrics","rmse", ... "Verbose",false, ... "Shuffle","every-epoch", ... "InitialLearnRate",0.001, ... "OutputNetwork","best-validation-loss", ... "ValidationData",{valData, ValRulData}, ... "ValidationFrequency",validationFrequency, ... "ValidationPatience",10, ... "ResetInputNormalization",false); rng("default") batteryNet = trainnet(trainData, trainRulData, layers, "mae", options);
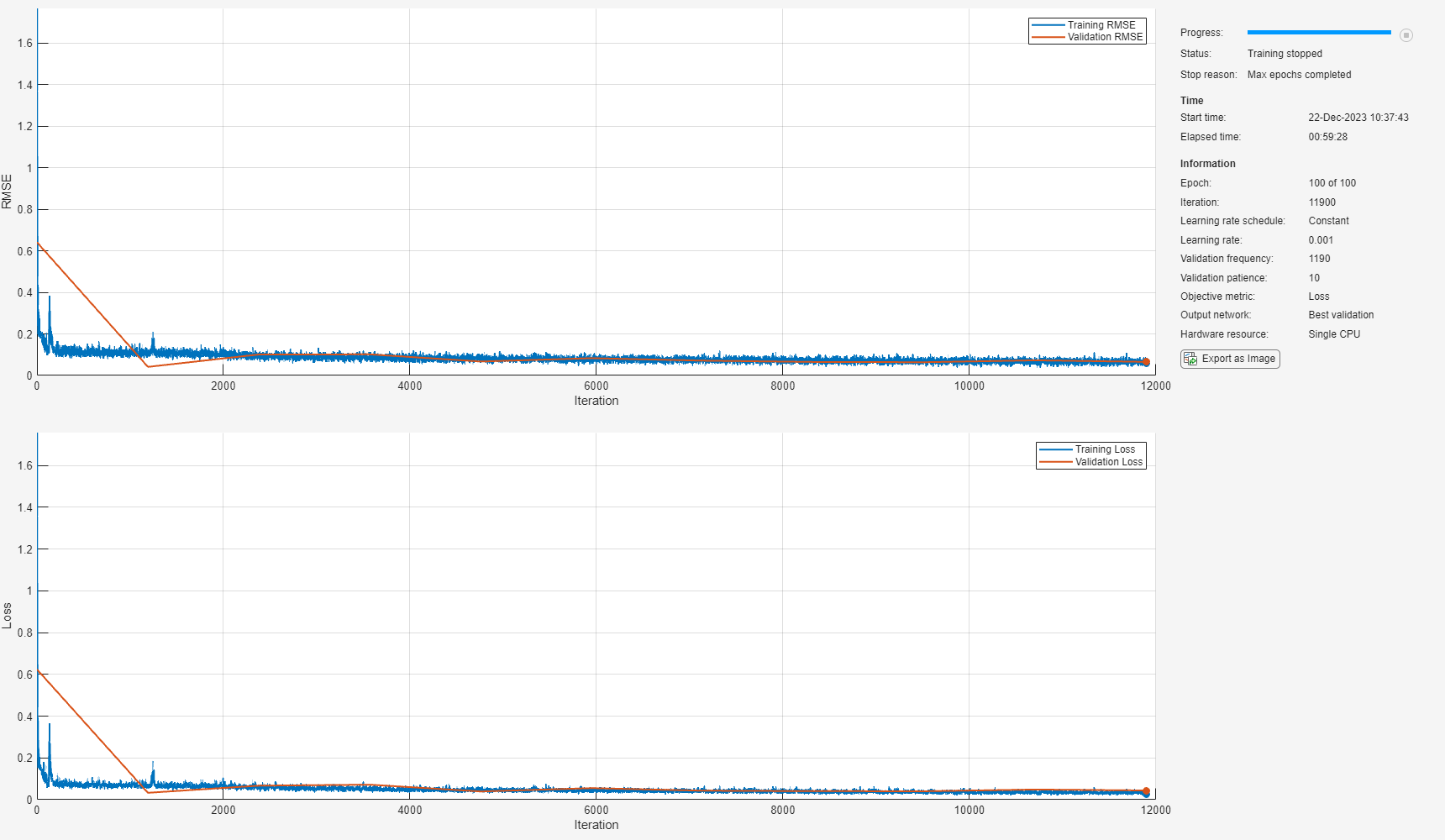
学習済みモデルのパフォーマンスを評価する
学習済みモデルを使用して、testData の残りのサイクル寿命を予測します。パフォーマンスを可視化しやすくするには、値を元の RUL 範囲に再スケーリングする必要があります。
yPredTest = predict(batteryNet,testData)*2000; testRulScaled = testRulData*2000;
散布図を使用して、実際のサイクル寿命と予測されたサイクル寿命を比較します。
figure; scatter(testRulScaled,yPredTest) hold on; refline(1,0); title("Predicted vs Actual Cycle Life") ylabel("Predicted cycle life"); xlabel("Actual cycle life");
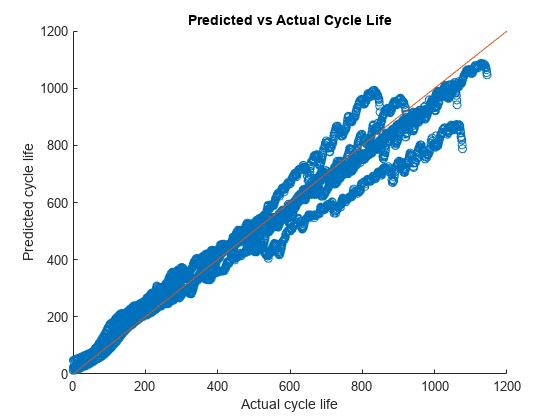
理想的には、散布図のすべてのデータ点が対角線に沿っていて、信頼区間が狭いことが望まれます。ただし、この例では、散布図のさまざまな範囲の値に対して、より広い拡散とさまざまな動作が見られます。散布図には、テスト データの各バッテリーに 1 つずつ、合計 5 つの異なるトレンドが示されています。
5 個のバッテリー全体で、実際のサイクル寿命が短い場合、モデルは残りの残存耐用期間を適切に予測します。この結果は、バッテリーの寿命が近づくにつれて、モデルが残りのサイクル寿命を適切に予測できるようになることを示唆しています。
ただし、実際のサイクル寿命が長いバッテリー寿命の初期段階では、モデルの不確実性が高くなります。また、このモデルは一般的に、バッテリー寿命の初期の残りのサイクル寿命を過大評価する傾向があります。これらのモデルの特徴に対処するには、より豊富で大規模なデータ セットを使用してネットワークを学習させ、深層ニューラル ネットワーク アーキテクチャとそのハイパーパラメーターを試すことができます。
予測された残りのサイクル寿命の平方根平均二乗誤差 (RMSE) と平均誤差率を計算します。
errTest = (yPredTest-testRulScaled); rmseTestModel = sqrt(mean(errTest.^2))
rmseTestModel = single
71.3987
n = numel(testRulScaled); nr = abs(testRulScaled - yPredTest); errVal = (1/n)*sum(nr./testRulScaled)*100
errVal = single
18.8414
これらの性能メトリクスは、初期動作データからのバッテリー サイクル寿命の予測 (Predictive Maintenance Toolbox)に示すように、正規化を伴う線形回帰モデルをカスタム機能とともに使用して残りのサイクル寿命を推定した場合の等価値に比較的近くなります。機械学習ベースの例では、最初の 100 サイクルのデータのみが残りのサイクル寿命の推定に使用されますが、この例では任意のサイクルのデータを使用できることに注意してください。この結果からは、アプリケーションとシステムの要件に応じて、機械学習と深層学習のいずれのアプローチを使用しても、バッテリーの残りのサイクル寿命の推定が可能であることが示唆されます。
モデルを目的の性能レベルに調整した後、モデルを運用可能にして、使用中のバッテリーの残りのサイクル寿命を推定できます。学習済みネットワークを組み込みハードウェアに展開するには、C/C++、GPU、または HDL コードを生成します。詳細については、コード生成と深層ニューラル ネットワークの展開を参照してください。学習済みネットワークをクラウドに展開するには、適切なパッケージ化オプションを選択します。
まとめ
この例では、40 個のバッテリーの測定値を基に、深層学習手法を使用してバッテリーのサイクル寿命を予測する方法を説明しました。生のセンサー信号は、特徴を手動で抽出することなく、深層ニューラル ネットワークに学習させるための入力として直接使用されます。このモデルをテスト データに対して使用し、性能評価を行いました。テスト データの測定値を使用すると、平均誤差率は約 16% です。
補助関数
function [dischargeData] = hExtractDischargeData(data) % HEXTRACTDISCHARGEDATA Extract measurements corresponding to discharge % portion of cycle dischargeData = cell(1, size(data, 2)); % For each battery in the data (which has many charge discharge cycles) for iBattery = 1:size(data,2) timeSeriesTable = struct2table(data(iBattery).cycles); % Keep only the data related to discharge [ between 3.6V and 2 V) clipIdxFun1 = @(x) {find(x{1,1}>=3.6,1,"last")}; clipIdxFun2 = @(x) {find(x{1,1}<=2.00,1,"first")}; clipIdx1 = rowfun(clipIdxFun1,timeSeriesTable,"InputVariables","V",... "OutputVariableNames","clipIdx1"); clipIdx2 = rowfun(clipIdxFun2,timeSeriesTable,"InputVariables","V",... "OutputVariableNames","clipIdx2"); timeSeriesTable = [timeSeriesTable clipIdx1 clipIdx2]; %#ok<AGROW> clipSignals = @(x,y,z) {smoothdata(x(y:z),"movmean",3)}; % Extract Voltage Vd = rowfun(clipSignals,timeSeriesTable,"InputVariables",... ["V","clipIdx1","clipIdx2"],"OutputVariableNames","Vd",... "ExtractCellContents",true); % Extract Temperature Td = rowfun(clipSignals,timeSeriesTable,"InputVariables",... ["T","clipIdx1","clipIdx2"],"OutputVariableNames","Td",... "ExtractCellContents",true); % Extract Discharge Capacity QdClipped = rowfun(clipSignals,timeSeriesTable,"InputVariables",... ["Qd","clipIdx1","clipIdx2"],"OutputVariableNames","QdClipped",... "ExtractCellContents",true); dischargeData{iBattery} = [Vd Td QdClipped]; end end function [Vdlin, Tdlin, Qdlin] = hLinearInterpolation(dischargeData) % HLINEARINTERPOLATION Interpolate on the voltage range of 2V to 3.6V % linear interpolation onto 900 points between the two voltages and the % data is then reshaped into a 30x30 matrix Vdlin = cellfun(@(x)rowfun(@hLinInterp,x,"InputVariables",["Vd","Vd"],... "OutputVariableNames","Vdlin","OutputFormat","cell"), dischargeData, ... 'UniformOutput', false); Tdlin = cellfun(@(x)rowfun(@hLinInterp,x,"InputVariables",["Vd","Td"],... "OutputVariableNames","Tdlin","OutputFormat","cell"), dischargeData, ... 'UniformOutput', false); Qdlin = cellfun(@(x)rowfun(@hLinInterp,x,"InputVariables",["Vd","QdClipped"],... "OutputVariableNames","Qdlin","OutputFormat","cell"), dischargeData, ... 'UniformOutput', false); end function xInterpolated = hLinInterp(volt,x) % HLININTERP Function to linearly interpolate data for battery voltage discharge range volt = volt{1,1}; x = x{1,1}; % Set seed for consistent results rng("default"); % Linearly interpolate voltage range 3.6 to 2. voltRange = linspace(3.6,2,900); [~, ia, ~] = unique(volt,'sorted'); f = griddedInterpolant(volt(ia),x(ia)); xInterpolated= reshape(f(voltRange)',[30,30]); end function [signalData, rul] = hreshapeData(VInterpol, TInterpol, QdInterpol) % HRESHAPEDATA Arrange the data as 30x30x3 - where each 30x30 is the 900 point % interpolated version for a single discharge and 3 is for V, Q, T for i =1:numel(VInterpol) VData = VInterpol{i}; TData = TInterpol{i}; QdData = QdInterpol{i}; predictor = zeros(30,30,3,size(VData,1)); for j = 1: size(VData,1) temp(:,:,1) = VData{j,1}; temp(:,:,2) = QdData{j,1}; temp(:,:,3) = TData{j,1}; predictor(:,:,:,j) = temp; end maxBatteryLife = 2000; % Used for scaling output numCycles = size(VData,1); cycle = (1:numCycles)'; rulBattery = (numCycles+1 - cycle)/maxBatteryLife; if i == 1 signalData = predictor; rul = rulBattery; else signalData = cat(4,signalData,predictor); rul = [rul; rulBattery]; %#ok<AGROW> end end end
参考文献
[1] Severson, K.A., Attia, P.M., Jin, N. et al. "Data-driven prediction of battery cycle life before capacity degradation." Nat Energy 4, 383–391 (2019). https://doi.org/10.1038/s41560-019-0356-8
参考
トピック
- 初期動作データからのバッテリー サイクル寿命の予測 (Predictive Maintenance Toolbox)
- 畳み込みニューラル ネットワークを使用した残存耐用期間の推定
- 劣化するバッテリー システムの非線形の状態推定 (Predictive Maintenance Toolbox)