3 次スプライン内挿

滑らかなデータの 3 次スプライン内挿

たとえば、以下に対して滑らかなデータを内挿すると仮定します。

rng(6), x = (4*pi)*[0 1 rand(1,15)]; y = sin(x);

次から得られる 3 次スプライン内挿を使用できます。

cs = csapi(x,y);

また、次のコードを使用して、スプラインをデータと共にプロットできます。

fnplt(cs);
hold on
plot(x,y,'o')
legend('cubic spline','data')
hold off

これにより、次のような Figure が生成されます。

滑らかなデータの 3 次スプライン内挿

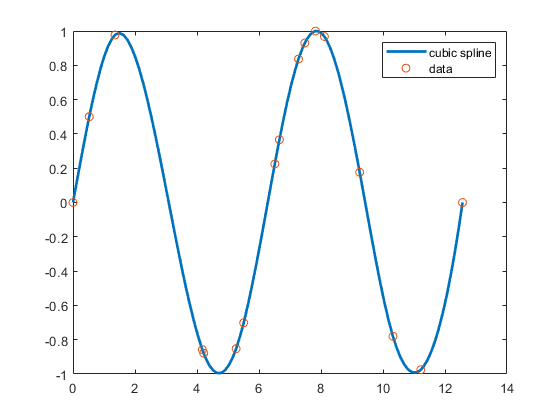
これは厳密にいえば、ノットなしの端点条件を使用する 3 次スプライン内挿です。つまり、左端と右端を除くすべての "内部" データ サイトでブレークを持つ 2 つの連続状態変数の微係数を使用する一意の区分的 3 次多項式です。これは、MATLAB^® spline コマンド spline(x,y) で生成されるものと同じ内挿です。

周期的データ

正弦関数は 2π 周期です。内挿がそのスコアでどの程度適切に機能しているか確認するには、たとえば、2 つの端点における 1 階微分値の差を計算します。

diff(fnval(fnder(cs),[0 4*pi]))
ans = -.0100

上記の場合はあまり適切とはいえません。2 つの端点 0 および 4*pi において 1 階微分と 2 階微分が一致する内挿を得たい場合は、代わりにコマンド csape を使用します。このコマンドを使用すると、周期的な端点条件を含むさまざまな端点条件を指定できます。したがって、代わりに次を使用します。

pcs = csape(x,y,'periodic');

次の結果が得られます。

diff(fnval(fnder(pcs),[0 4*pi]))

出力は、端点の傾きの差として ans = 0 となります。端点の 2 階微分の差が小さい場合でも、

diff(fnval(fnder(pcs,2),[0 4*pi]))

出力は ans = -4.6074e-015 となります。

その他の端点条件

他の端点条件にも対応できます。以下に例を示します。

cs = csape(x,[3,y,-4],[1 2]);

このようにすると、 にブレークがあり、左端のデータ サイトにおける傾きが 3、右端のデータ サイトにおける 2 階微分が -4 である 3 次スプライン内挿が得られます。

一般的なスプライン内挿

簡易なノットを使用して、ブレーク以外のサイトでまたは 3 次スプライン以外のスプラインにより内挿する場合は、spapi コマンドを使用します。最も簡易な形式は、sp = spapi(k,x,y) です。この場合、最初の引数である k には、内挿スプラインの "次数" を指定します。これは、多項式の各区分の係数の数、つまりその多項式の各区分のノミナル次数に 1 を加えた数を表します。たとえば、次に示す Figure はデータの 1 次、2 次および 4 次スプライン内挿を示します。これは以下のステートメントから得られます。

sp2 = spapi(2,x,y); fnplt(sp2,2), hold on
sp3 = spapi(3,x,y); fnplt(sp3,2,'k--'), 
sp5 = spapi(5,x,y); fnplt(sp5,2,'r-.'), plot(x,y,'o')
legend('linear','quadratic','quartic','data'), hold off

滑らかなデータのさまざまな次数のスプライン内挿

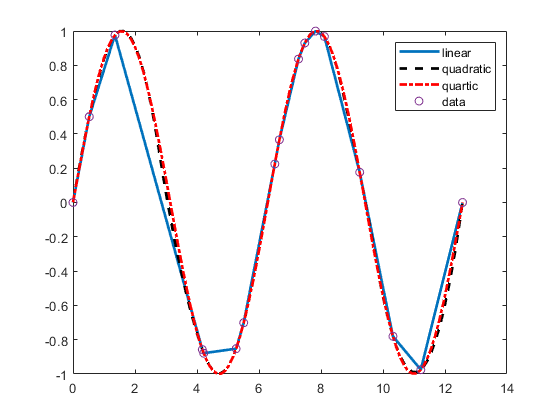
spapi から得られた 3 次スプライン内挿も、csapi および spline から返される 3 次元スプライン内挿とは異なります。それらの差を強調するために、プロットとその 2 階微分を次のように計算します。

fnplt(fnder(spapi(4,x,y),2)), hold on,
fnplt(fnder(csapi(x,y),2),2,'k--'),plot(x,zeros(size(x)),'o')
legend('from spapi','from csapi','data sites'), hold off

これにより、次のグラフが得られます。

同一の滑らかなデータの 2 つの 3 次スプライン内挿の 2 階微分

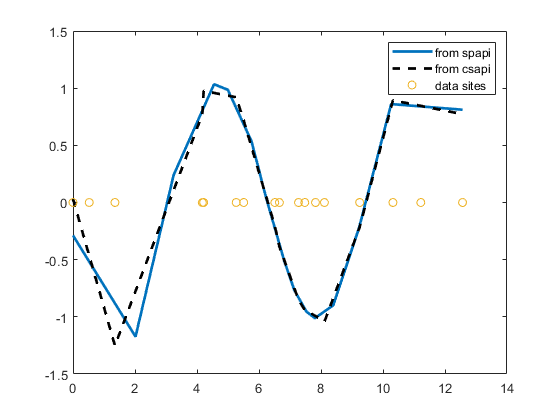
3 次スプラインの 2 階微分が、スプラインのブレークに頂点をもつ破線であることから、csapi ではデータ サイトにブレークが配置されるが、spapi では配置されないことがはっきりわかります。

ノットの選択

実際、スプライン内挿がブレークを持つ場所を、コマンド sp = spapi(knots,x,y) を使って明示的に指定できます。このコマンドでは、シーケンス knots で、使用するブレークを特定の方法で指定します。たとえば、sin(x) にする y を選択したときに、以下のコマンドを使用しました。

ch = spapi(augknt(x,4,2),[x x],[y cos(x)]);

上記のコマンドによって、正弦関数 (区分的三次関数) に対する 3 次エルミート内挿が得られます。これは、すべての x(i)' にブレークを持ち、値の正弦関数 "および" すべての x(i) における傾きと一致します。これにより、内挿は連続的な 1 階微分と連続的になりますが、通常、その 2 階微分のブレーク間ではジャンプします。このコマンドは、データ値配列 [y cos(x)] のどの部分で値が指定され、どの部分で傾きが指定されるかをどのように認識するのでしょうか。ここに示すデータ サイト配列は [x x] として指定されています。つまり、各データ サイトが 2 回示されている点に注目してください。また、y(i) が 1 つ目の x(i) の出現箇所に関連付けられ、cos(x(i)) が 2 つ目の x(i) の出現箇所に関連付けられていることにも注目してください。1 つ目のデータ サイトに関連付けられているデータ値は関数値として使用されます。2 つ目のデータ サイトに関連付けられているデータ値は傾きとして使用されます。3 つ目のデータ サイトがある場合、対応するデータ値はそのサイトで一致する 2 階微分値と見なされます。ここで使用するコマンド augknt を使用して適切な "ノット シーケンス" を生成する方法については、B 型スプラインの作成と操作を参照してください。

平滑化

データのノイズが多い場合は、どのように対処するのでしょうか。たとえば、次の値が与えられているとします。

noisy = y + .3*(rand(size(x))-.5);

この場合は、代わりに近似することができます。たとえば、次のコマンドで得られる 3 次平滑化スプラインを試してみるとします。

scs = csaps(x,noisy);

これは次のコマンドでプロットされます。

fnplt(scs,2), hold on, plot(x,noisy,'o'),
legend('smoothing spline','noisy data'), hold off

これにより次のような Figure が生成されます。

ノイズの多いデータの 3 次平滑化スプライン

csaps(x,y) により実行される平滑化のレベルが十分でない場合は、平滑化パラメーター p をオプションの 3 つ目の引数として指定してそのレベルを変更できます。この数値を 0 ～ 1 の間で選択します。p が 0 から 1 に変更されると、平滑化スプラインもそれに合わせて一端 (データの最小二乗直線近似) からもう一方の端 (データの "自然な" 3 次スプライン内挿) に変わります。csaps は、オプションの 2 つ目の出力として実際に使用された平滑化パラメーターを返すため、次のように試すことができます。

[scs,p] = csaps(x,noisy); fnplt(scs,2), hold on
fnplt(csaps(x,noisy,p/2),2,'k--'), 
fnplt(csaps(x,noisy,(1+p)/2),2,'r:'), plot(x,noisy,'o')
legend('smoothing spline','more smoothed','less smoothed',...
'noisy data'), hold off

これによって以下の図が生成されます。

いくらか平滑化された、ノイズの多いデータ

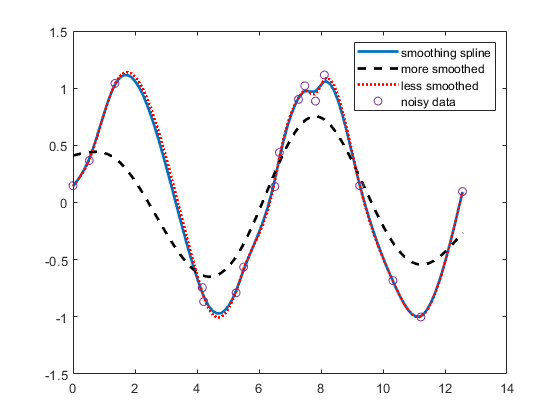
単純に、norm(noisy - fnval(sp,x))^2 <= tol において特定のデータの指定された許容誤差 tol 内で最も滑らかな 3 次スプライン sp を得る必要がある場合があります。このスプラインは、定義された許容誤差 tol に対してコマンド sp = spaps(x,noisy,tol) を使用して作成します。

最小二乗法

最小二乗近似を選択する場合は、ステートメント sp = spap2(knots,k,x,y) で得ることができます。このステートメントでは、スプラインのノット シーケンス knots と次数 k の両方を指定しなければなりません。

次数の一般的な選択肢は 4 で、3 次スプラインが与えられます。ノットの選択方法を明確に決めていない場合、使用する多項式区分の数を指定します。以下に例を示します。

sp = spap2(3,4,x,y); 

3 つの多項式区分で構成される 3 次スプラインが与えられます。結果の誤差が不均等である場合は、次のように newknt を使用してより適切なノットの分布になるよう試すことができます。

sp = spap2(newknt(sp),4,x,y);