チェビシェフ スプラインの作成

この節では、チェビシェフ スプラインの作成の次の点について説明します。

• チェビシェフ スプラインとは

• スプライン空間の選択

• 初期推定

• Remez 反復

チェビシェフ スプラインとは

節点シーケンス t=(t_i: i=1:n+k) の場合の、次数 k の "チェビシェフ" スプライン C=C_t=C_k,t は、最大ノルム 1 の S_k,t の固有の要素で、区間 [t_k..t_n+1] で最大限変動し、t_n+1 に近い正数です。つまり、C(τ_i)=(–1)^{n – 1} (すべての i について) によって与えられる関数 C=C_t∊S_k,t が [t_k.t_n+1] で最大ノルム 1 をもつように、厳密に増加する固有の n シーケンス τ が存在します。これは、τ₁=t_k,τ_n=t_n+1、および t_i < τ_i < t_k+i (すべての i について) を意味しています。事実、t_i+1 ≤ τ_i ≤ t_i+k–1 (すべての i について) です。これにより、このような不等式が節点シーケンスにより可能になると想定される、つまり、S_k,t の要素が連続していると想定されるという論点が生まれます。

要するに、チェビシェフ スプライン C は、チェビシェフ多項式のように見えます。同様の機能を実行します。たとえば、その極端なサイト τ は、結果の射影子のノルムがほぼ最小限であるため、S_k,t から内挿するのに特に適したサイトです。ツールボックス コマンド chbpnt を参照してください。

例チェビシェフ スプラインの作成を実行して、特定の節点シーケンス t の C を作成できます。

スプライン空間の選択

3 次スプラインを取り上げます。つまり、次数は以下のとおりです。

k = 4;

以下のブレーク シーケンスを使用します。

breaks = [0 1 1.1 3 5 5.5 7 7.1 7.2 8];
lp1 = length(breaks); 

簡易な内部節点を使用します。つまり、以下の節点シーケンスを使用します。

t = breaks([ones(1,k) 2:(lp1-1) lp1(:,ones(1,k))]);
n = length(t)-k;

各端点の四倍の節点に注意してください。k = 4 のため、これは、[0..8] = [breaks(1)..breaks(lp1)] を対象の区間 [t_k..t_n+1] にします。n = length(t)-k は結果のスプライン空間 S_k,t の次元です。以下の場合にも、同じ節点シーケンスが提供されます。

t=augknt(breaks,k);

初期推定

τ の初期推定として、節点平均を使用します。

$$t_i=(t_{i+1}+\mathrm{...}+t_{i+k-1})/(k-1)$$

これは、適切な内挿サイト選択として推奨されています。これらは、以下によって提供されます。

tau=aveknt(t,k); 

結果として得られた C への最初の近似、つまり、c(τ_i)=(–1)^n-–i (すべての i について) を満たすスプライン c をプロットします。

b = cumprod(repmat(-1,1,n)); b = b*b(end);
c = spapi(t,tau,b); 
fnplt(c,'-.') 
grid

以下のプロットが得られます。

チェビシェフ スプラインへの最初の近似

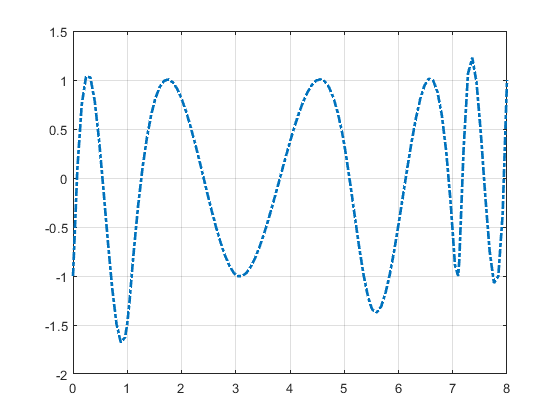
Remez 反復

この近似から始めて、Remez アルゴリズムを使用して C に収束する一連のスプラインを生成できます。つまり、C への現在の近似 c の極値として新しい τ を作成し、再度試行します。ここでは、ループ全体です。

Dc のゼロ、つまり、c の 1 階微分として新しい内部 τ_i を求めます。最初に微分します

Dc = fnder(c);

関数 fnzeros を使用して、Dc のゼロをとります。このゼロは、現在の近似 c の極値を表します。この結果が tau の新しい推定となります。

tau(2:n-1) = mean(fnzeros(Dc));

その後、現在の近似の極値を確認します。

extremes = abs(fnval(c, tau));

差分

max(extremes)-min(extremes)
  ans = 0.6906

は、全体の平準化からいかに離れているかの推定です。

新しく選択した tau に対応する新しいスプラインを作成し、それを以前のスプラインの上にプロットします。

c = spapi(t,tau,b); 
sites = sort([tau (0:100)*(t(n+1)-t(k))/100]); 
values = fnval(c,sites); 
hold on, plot(sites,values)

以下のコードは、グリッドをオンにし、極値の位置をプロットします。

grid on
plot(tau(2:end-1),zeros(size(tau(2:end-1))),'o');
hold off
lgd = legend( 'Initial Guess', 'Current Guess', 'Extreme Locations',...
 'location', 'NorthEastOutside' );
lgd.Location = 'south';

以下は結果の Figure です (凡例は示されていません)。

ほぼ平準化されたスプライン

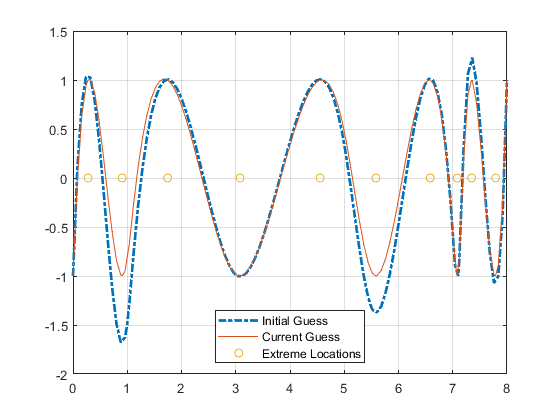
これが十分に近接していない場合は、単にループを繰り返します。この例では、次の反復が既にグラフィックスの精度に対する C を生成しています。