chbpnt

チェビシェフ・デムコ点

構文

tau = chbpnt(t,k)
chbpnt(t,k,tol)
[tau,sp] = chbpnt(...)


説明

tau = chbpnt(t,k) は、ノット シーケンス t をもつ次数 k のチェビシェフ スプラインの極端なサイトです。これらは特に、ノット シーケンス t をもつ次数 k のスプラインによってデータが内挿される場合に適したサイトです。それは、結果の内挿が、通常、スプライン空間から、tau で内挿される値をもつ関数への最適で一様な近似にきわめて近くなるからです。

chbpnt(t,k,tol) は、チェビシェフ スプラインを作成する反復プロセスで使用される許容誤差 tol も指定します。このプロセスは、スプラインの絶対最大局所的極値と絶対最小局所的極値の相対差分が tol より小さくなると終了します。tol の既定値は .001 です。

また、[tau,sp] = chbpnt(...) は、sp でチェビシェフ スプラインも返します。

例

平方根関数の近似

関数augkntを使用して、0 が 10 個と 1 が 10 個のノット シーケンスを作成します。

k = 10;
t = augknt([0,1],k);

ノット シーケンス t をもつ次数 10 のチェビシェフ スプラインのチェビシェフ・デムコ点を計算することによって、内挿サイトのベクトルを作成します。

sites = chbpnt(t,k);

チェビシェフ・デムコ点で関数sqrtを評価することによって、内挿点のベクトルを作成します。関数spapiを使用して、評価された点間をノット シーケンス t から 10 次スプラインで内挿します。t 内のノットは、スプライン近似が、0 と 1 で境界をもつ単一の多項式で構成されることを示しています。

interpolationPoints = sqrt(sites);
sp = spapi(t,sites,interpolationPoints)

sp = struct with fields:
      form: 'B-'
     knots: [0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1]
     coefs: [-4.2719e-17 0.8842 -0.7101 2.4484 -1.1869 1.9678 0.3331 0.9940 0.9349 1]
    number: 10
     order: 10
       dim: 1

構造体 sp には、スプラインのプロパティが含まれます。sp の coefs フィールドは、区間 [0,1] で平方根関数を近似する多項式の係数ベクトルです。

sp と平方根関数を同じプロット内に表示して比較します。

x = linspace(0,1,1000);

plot(x,sqrt(x))
hold on
fnplt(sp,'-',0.75)
legend(["square root function" "spline"],Location="best")

プロットは、スプラインが平方根関数に密接に追従していることを示しています。

ルンゲ関数の内挿点の比較

ルンゲ関数の無名関数を作成し、区間 [-1 1] でプロットします。

runge = @(x) 1./(1+25*x.^2);
figure
hold on
fplot(runge,[-1 1],"k",LineWidth=2);

augkntとlinspaceを使用して、区間 [-1 1] におけるノット シーケンスと等間隔の内挿点を作成します。組み込みのルンゲ関数 runge を内挿点で評価します。

k = 11;
t = augknt([-1 1],k);
x_es = linspace(-0.99,0.99,k);
y_es = runge(x_es);

ノット シーケンス t をもつ次数 10 の多項式スプラインを等間隔の内挿点に当てはめます。

sp_es = spapi(t,x_es,y_es)

sp_es = struct with fields:
      form: 'B-'
     knots: [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 1 1 1 1 1 1 1]
     coefs: [-0.8586 19.5179 -73.4835 169.6651 -275.4870 326.3246 -275.4870 169.6651 -73.4835 19.5179 -0.8586]
    number: 11
     order: 11
       dim: 1

sq_es は近似の結果を格納する struct です。フィールド coefs に次数 10 の多項式の係数が格納されます。

runge、sp_es、および内挿点を区間 [-1 1] でプロットします。

figure
hold on
fplot(runge,[-1 1],"k",LineWidth=2);
plot(x_es,y_es,"ro")
fnplt(sp_es,[-1 1],"r",1)

プロットは、区間の境界近くで sp_es に大きな振動があることを示しています。

近似を改善するために、chbpnt を使用して、ノット シーケンス t をもつ次数 10 のチェビシェフ スプラインのチェビシェフ・デムコ内挿点を求めます。

x_cd = chbpnt(t,k);
y_cd = runge(x_cd);

ノット シーケンス t を使用してチェビシェフ・デムコ内挿点にスプラインを当てはめます。

sp_cd = spapi(t,x_cd,y_cd)

sp_cd = struct with fields:
      form: 'B-'
     knots: [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 1 1 1 1 1 1 1]
     coefs: [0.0385 0.2641 -2.5533 12.9011 -32.4456 46.7434 -32.4456 12.9011 -2.5533 0.2641 0.0385]
    number: 11
     order: 11
       dim: 1

sq_cd にチェビシェフ・デムコ内挿点の近似の結果が格納されます。

runge、sp_cd、および内挿点を区間 [-1 1] でプロットします。

figure
hold on
fplot(runge,[-1 1],"k",LineWidth=2);
plot(x_cd,y_cd,"ro")
fnplt(sp_cd,[-1 1],"r",1)

プロットは、sp_cd に sp_eq ほど大きな振動がないことを示しています。sp_cd の方が区間の境界近くで runge を適切に近似しています。

スプラインの精度を比較するには、区間 [-1 1] 内の 1000 個の等間隔の点で runge を評価します。fnvalを使用して sp_es と sp_cd を同じ点で評価します。

i = linspace(-1,1,1000);
runge_val = runge(i);
sp_es_val = fnval(sp_es,i);
sp_cd_val = fnval(sp_cd,i);

関数normを使用して sp_es と sp_cd の誤差二乗和 ("SSE") を計算します。

error_es = sp_es_val - runge_val;
error_cd = sp_cd_val - runge_val;

[norm(error_es)^2 norm(error_cd)^2]

ans = 1×2

  324.0260    3.8479

sp_cd の方が "SSE" が小さく、チェビシェフ・デムコ内挿点の方が等間隔の内挿点よりも全体的に runge を適切に近似していることを示しています。

アルゴリズム

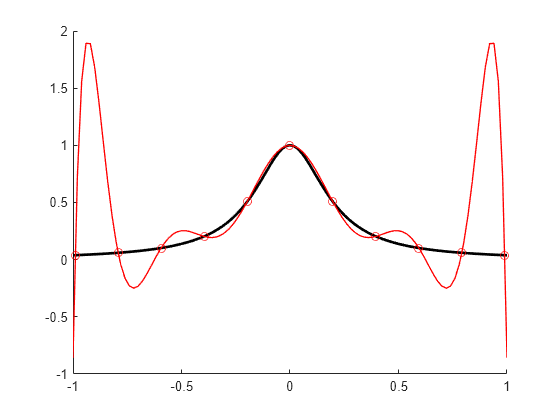
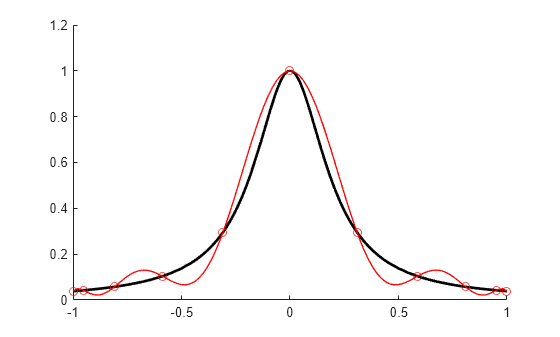
与えられたノット シーケンスと次数のチェビシェフ スプラインは、Remez アルゴリズムを使用して反復的に作成されます。初期推定として、シーケンス aveknt(t,k) で値 1 と −1 を交互にとるスプラインを使用します。例チェビシェフ スプラインの作成では、特定の例に適用された場合のプロセスのバージョンの 1 つが詳しく説明されています。

参考

aveknt