周波数領域の仕様

この例では、制御システムを systune または looptune で調整するために使用できる周波数領域の要件を示します。

関数 systune と looptune は、時間領域と周波数領域のさまざまな要件に従って固定構造制御システムのパラメーターを調整します。それらの要件を指定するには、調整目標オブジェクトを使用します。

ゲインの範囲

TuningGoal.Gain 要件では、SISO または MIMO の閉ループ伝達関数にゲインの範囲を適用します。この要件は、適切な外乱の抑制とロールオフの適用、感度と制御操作の制限、飽和の回避に役立ちます。MIMO 伝達関数の場合、"ゲイン" は周波数応答行列の最大特異値を指します。ゲインの範囲は周波数に依存します。以下に例を示します。

s = tf('s');
R1 = TuningGoal.Gain('d','y',s/(s+1)^2);

これは、d から y へのゲインが伝達関数 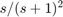$s/(s+1)^2$ の振幅を超えないようにすることを指定しています。

viewGoal(R1)

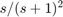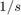多くの場合、目的のゲインプロファイルの漸近線をスケッチすると便利です。たとえば、伝達関数 $s/(s+1)^2$ の代わりに、周波数 0.01、1、100 でのゲイン値 0.01、1、0.01 を単純に指定できます。点 (1,1) が 2 つの漸近線 $s$ および $1/s$ のブレークポイントになります。

Asymptotes = frd([0.01,1,0.01],[0.01,1,100]);
R2 = TuningGoal.Gain('d','y',Asymptotes);

要件オブジェクトによって、この離散ゲインプロファイルがすべての周波数で定義されたゲインの範囲に自動的に変換されます。

bodemag(Asymptotes,R2.MaxGain)
legend('Specified','Interpolated')

分散増幅

TuningGoal.Variance 要件では、指定した入力から指定した出力へのノイズ分散増幅を制限します。専門用語で言うと、この要件では閉ループ伝達関数の 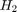$H_2$ ノルムを制約します。入力信号がランダム過程であり、平均ゲインがピークゲインよりも重要な場合は、TuningGoal.Gain ではなくこの要件を使用することをお勧めします。以下に例を示します。

R = TuningGoal.Variance('n','y',0.1);

これは、単位分散ホワイトノイズ入力 n に対し y の出力分散を $0.1^2$ に制限しています。

設定値追従とオーバーシュートの削減

TuningGoal.Tracking 要件では、周波数領域で設定値追従とループの分離という目的を適用します。以下に例を示します。

R1 = TuningGoal.Tracking('r','y',2);

これは、出力 y が 2 秒の応答時間で基準 r を追従するように指定しています。同様に、

R2 = TuningGoal.Tracking({'Vsp','wsp'},{'V','w'},2);

これは、2 つの応答間の相互干渉を最小限に抑えながら V が Vsp を、w が wsp を追従するように指定しています。追従要件は、周波数の関数としての追従誤差に対する周波数領域の制約に変換されます。たとえば、1 つ目の要件 R1 の場合、r から追従誤差 e = r-y へのゲインは低周波数では小さく、周波数が 1 rad/s (2 秒の応答時間の帯域幅) を超えると 1 (100%) に近づきます。viewGoal を使用してこの周波数領域の制約を可視化できます。黄色の領域は要件が満たされない部分を示します。

viewGoal(R1)

応答のオーバーシュートが過剰な場合は、TuningGoal.Overshoot 要件と TuningGoal.Tracking 要件を組み合わせて使用します。たとえば、次を使用して r から y へのオーバーシュートを 10% に制限できます。

R3 = TuningGoal.Overshoot('r','y',10);

外乱の抑制

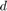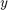図 1 に示すようなフィードバックループでは、外乱 $d$ から出力 $y$ への開ループ応答と閉ループ応答は次のような関係になります。

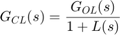
$G_{CL} (s) = { G_{OL} (s) \over 1 + L(s) }$

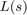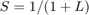ここで、 $L(s)$ は外乱のエントリポイントで測定されたループ伝達関数です。 $1+L$ のゲインは、外乱に対する開ループの感度と閉ループの感度の比率である外乱減衰係数です。その逆数 $S = 1/(1+L)$ は、外乱入力における感度です。

図 1: サンプルフィードバックループ

TuningGoal.Rejection 要件では、外乱抑制を周波数の関数として指定します。フィードバック制御によって外乱の影響が緩和されるため、減衰係数は制御帯域幅内で 1 を超えます。原則的に、抑制を 10 倍にするにはループゲインを 10 倍にしなければなりません。以下に例を示します。

R1 = TuningGoal.Rejection('u',10);
R1.Focus = [0 1];

これは、プラント入力 "u" に入る外乱が 0 ～ 1 rad/s の周波数帯域で 10 倍抑制されるように指定しています。

viewGoal(R1)

より一般的には、次のように周波数依存の抑制プロファイルを指定できます。

s = tf('s');
R2 = TuningGoal.Rejection('u',(s+10)/(s+0.1));

これは、0.1 rad/s 未満で 100 の減衰係数が徐々に下がり、10 rad/s を超えると 1 (減衰なし) になるように指定しています。

viewGoal(R2)

最小 attenuation を指定する代わりに、TuningGoal.Sensitivity 要件を使用して最大感度、つまり 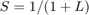$S = 1/(1+L)$ の最大ゲインを指定できます。以下に例を示します。

R3 = TuningGoal.Sensitivity('u',(s+0.1)/(s+10));

これは、前述の抑制要件 R2 と等価です。感度は 0.1 rad/s 未満で 0.01 (1%) であり、そこから増加して 10 rad/s を超えると 1 (100%) になります。

viewGoal(R3)

周波数重み付けゲインと周波数重み付け分散

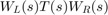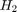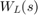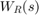TuningGoal.WeightedGain 要件と TuningGoal.WeightedVariance 要件は、TuningGoal.Gain 要件と TuningGoal.Variance 要件を一般化したものです。これらの要件では、周波数重み付け閉ループ伝達関数 $W_L(s) T(s) W_R(s)$ の $H_\infty$ ノルムまたは $H_2$ ノルムを制約します。ここで、 $W_L(s)$ と $W_R(s)$ はユーザー定義の重み付け関数です。たとえば、次の正規化ゲインの制約を指定します。

$\left\| \left( \begin{array}{c} {1 \over s+0.001} T_{re} \\ {s \over 0.001s+1} T_{ry} \end{array} \right) \right\|_\infty < 1$

WL = blkdiag(1/(s+0.001),s/(0.001*s+1));
WR = [];
R = TuningGoal.WeightedGain('r',{'e','y'},WL,[]);

viewGoal(R)

参考