時間領域の仕様
この例では、制御システムを systune または looptune で調整するために使用できる時間領域の要件について説明します。
関数 systune と looptune は、時間領域と周波数領域のさまざまな要件に従って固定構造制御システムのパラメーターを調整します。それらの要件を指定するには、調整目標オブジェクトを使用します。
ステップ コマンドの追跡
TuningGoal.StepTracking 要件では、調整された閉ループ システムがステップ入力にどのように応答するかを指定します。目的の応答を 1 次特性または 2 次特性で指定するか、明示的な参照モデルとして指定することができます。この要件は、実際の応答と目的の応答の間の相対ギャップが最小二乗の意味で十分に小さい場合に満たされます。以下に例を示します。
R1 = TuningGoal.StepTracking('r','y',0.5);
これは、r から y への閉ループ応答が、時定数 0.5 の 1 次システムのように動作することを求めています。
R2 = TuningGoal.StepTracking('r','y',zpk(2,[-1 -2],-1));
これは、2 次の非最小位の動作を指定しています。viewGoal を使用して目的の応答を可視化します。
viewGoal(R2)
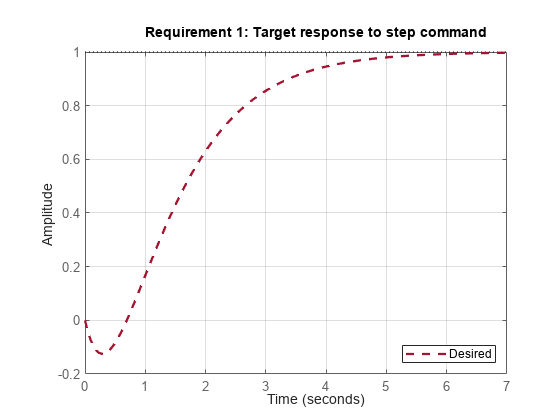
この要件は、SISO と MIMO の両方のステップ応答の調整に使用できます。MIMO の場合は、この要件によって、各出力が対応する入力を最小限の相互干渉で追従するようになります。
ステップ外乱の抑制
TuningGoal.StepRejection 要件では、調整された閉ループ システムがステップ外乱にどのように応答するかを指定します。応答振幅、整定時間および振動の減衰の最悪値を指定できます。以下に例を示します。
R1 = TuningGoal.StepRejection('d','y',0.3,2,0.5);
これは、 の振幅を 0.3、整定時間を 2 時間単位、減衰比を最小で 0.5 に制限しています。viewGoal を使用して対応する時間応答を表示します。
viewGoal(R1)
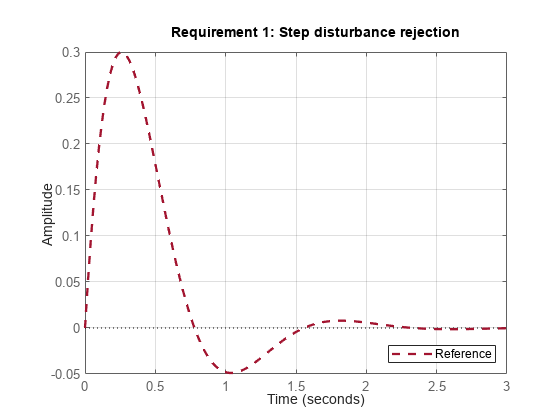
"参照モデル" を使用して目的の応答を指定することもできます。外乱の抑制を改善できる場合、実際の応答と指定した応答は大幅に異なる可能性があります。ほぼ一致するのが望ましい場合は、TuningGoal.Transient 要件を使用します。最適な結果を得るには、実際の応答と指定した応答が同様のピーク振幅をもつように参照モデルのゲインを調整します (詳細については、TuningGoal.StepRejection のドキュメンテーションを参照してください)。
過渡応答の一致
TuningGoal.Transient 要件では、特定の入力信号に対する過渡応答を指定します。これは TuningGoal.StepTracking 要件を一般化したものです。以下に例を示します。
R1 = TuningGoal.Transient('r','y',tf(1,[1 1 1]),'impulse');
これは、 から への調整された応答が参照モデル のインパルス応答のようになることを求めています。
viewGoal(R1)
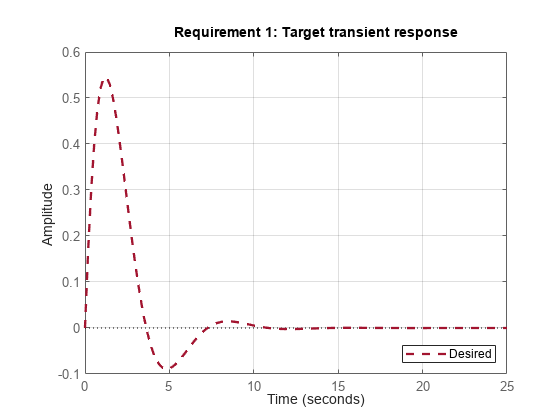
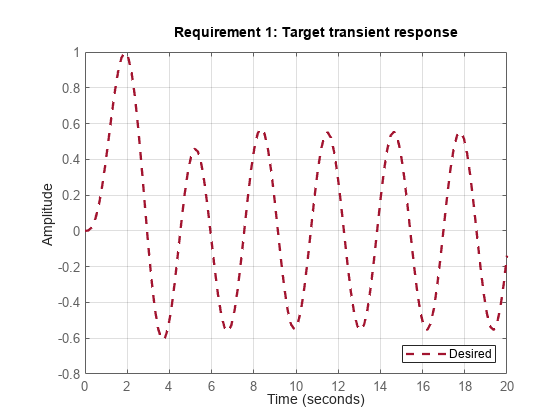
入力信号は、インパルス、ステップ、ランプ、一部の入力整形フィルターのインパルス応答としてモデル化されたより一般的な信号のいずれかにすることができます。たとえば、周波数が の正弦波を のインパルス応答としてモデル化できます。
w0 = 2; F = tf(w0^2,[1 0 w0^2]); % input shaping filter R2 = TuningGoal.Transient('r','y',tf(1,[1 1 1]),F); viewGoal(R2)
LQG 設計
TuningGoal.LQG 要件を使用して、制御システムのパラメーターを調整するための線形 2 次ガウシアン目的を作成します。この目的は、LQG 制御の標準的なオブザーバー構造だけでなく、任意の制御構造に適用できます。たとえば、図 2 のシンプルな PID ループについて考えます。ここで、 と は単位分散の外乱入力とノイズ入力で、 と は外乱とノイズのスペクトル成分をモデル化するローパス フィルターとハイパス フィルターです。
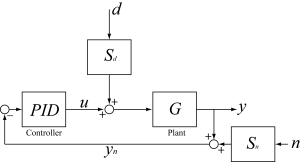
図 2: 制御ループ
をゼロ近傍に制御するには、次の LQG 基準を使用できます。
積分の第 1 項は のゼロからの偏差を抑制し、第 2 項は制御操作を抑制します。systune を使用して、コスト が最小限に抑えられるように PID コントローラーを調整できます。これを行うには、次の LQG 要件を使用します。
Qyu = diag([1 0.05]); % weighting of y^2 and u^2 R4 = TuningGoal.LQG({'d','n'},{'y','u'},1,Qyu);
参考
TuningGoal.StepTracking | TuningGoal.StepRejection | TuningGoal.Transient | TuningGoal.LQG