ジェット機のヨー ダンパーの設計
このケース スタディの概要
このケース スタディでは、747® ジェット機のヨー ダンパーの設計を通して、古典制御設計用ツールの使用方法を示します。
ジェット モデルの作成
マッハ 0.8、高度 40,000 フィートで飛行中のジェット モデルは、次のように表せます。
A=[-.0558 -.9968 .0802 .0415;
.598 -.115 -.0318 0;
-3.05 .388 -.4650 0;
0 0.0805 1 0];
B=[ .00729 0;
-0.475 0.00775;
0.153 0.143;
0 0];
C=[0 1 0 0;
0 0 0 1];
D=[0 0;
0 0];
sys = ss(A,B,C,D);次のコマンドでは、LTI オブジェクトとして、この状態空間モデルを設定し、状態、入力、および出力に名前を付けます。
states = {'beta' 'yaw' 'roll' 'phi'};
inputs = {'rudder' 'aileron'};
outputs = {'yaw' 'bank angle'};
sys = ss(A,B,C,D,'statename',states,...
'inputname',inputs,...
'outputname',outputs);
「sys」と入力すると、LTI モデル sys を表示できます。このコマンドにより以下の結果が出力されます。
a =
beta yaw roll phi
beta -0.0558 -0.9968 0.0802 0.0415
yaw 0.598 -0.115 -0.0318 0
roll -3.05 0.388 -0.465 0
phi 0 0.0805 1 0
b =
rudder aileron
beta 0.00729 0
yaw -0.475 0.00775
roll 0.153 0.143
phi 0 0
c =
beta yaw roll phi
yaw 0 1 0 0
bank angle 0 0 0 1
d =
rudder aileron
yaw 0 0
bank angle 0 0
Continuous-time model.モデルには、2 つの入力と 2 つの出力があります。単位は、beta (横すべり角) と phi (バンク角) に対してはラジアン、yaw (ヨー レート) と roll (ロール レート) に対してはラジアン/秒です。方向舵および補助翼の偏向角の単位もラジアンです。
開ループ極の計算
開ループ極を計算し、それらを s 平面にプロットします。
>> damp(sys)
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-7.28e-03 1.00e+00 7.28e-03 1.37e+02
-5.63e-01 1.00e+00 5.63e-01 1.78e+00
-3.29e-02 + 9.47e-01i 3.48e-02 9.47e-01 3.04e+01
-3.29e-02 - 9.47e-01i 3.48e-02 9.47e-01 3.04e+01
pzmap(sys)

このモデルには、減衰率の小さな極が 1 組あります。これらは、ダッチ ロール モードと呼ばれるモードに相当します。
これらの極の減衰を増加するような補償器を設計して、複素数の極が固有振動数 ωn < 1 ラジアン/秒、減衰率 ζ > 0.35 となるようにします。これには、Control System Toolbox™ の解析ツールを使用できます。
開ループ解析
まず、開ループ解析を行って可能な制御戦略を決定します。最初に時間応答を解析します (ここでは、関数 step または impulse を使用します)。
impulse(sys)
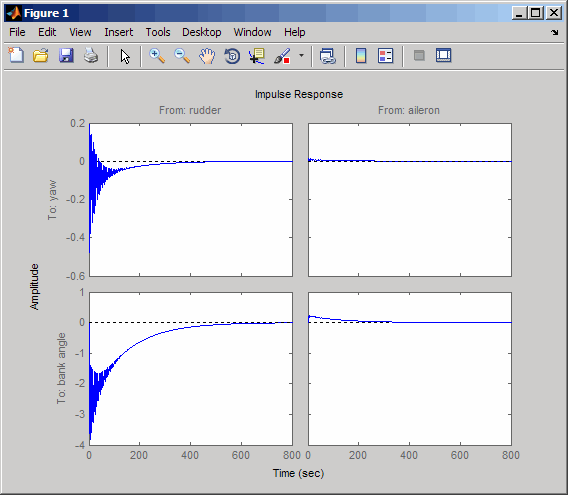
インパルス応答からシステムがやや減衰していることがわかります。ただし、乗客とパイロットは、最初の数分間ではなく、最初の数秒間の挙動に関心があるため、この時間枠は長すぎます。次に、20 秒という短い時間枠での応答を確認します。
impulse(sys,20)
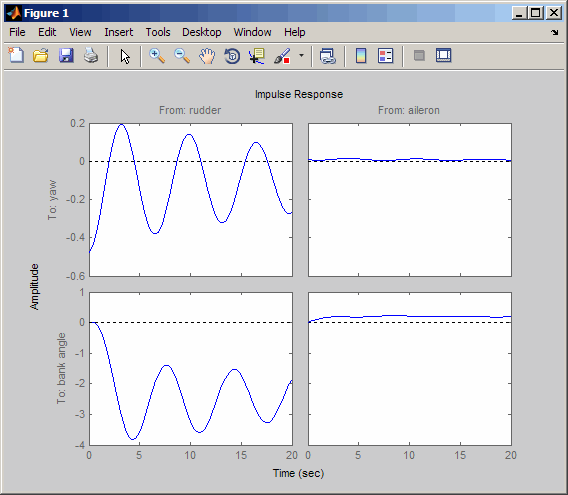
補助翼 (入力 2) からバンク角 (出力 2) へのプロットを確認します。このプロットのみを表示するには、右クリックして [I/O セレクター] を選択してから、(2,2) をクリックします。I/O セレクターは、次のようになります。
次のような新しい図が表示されます。
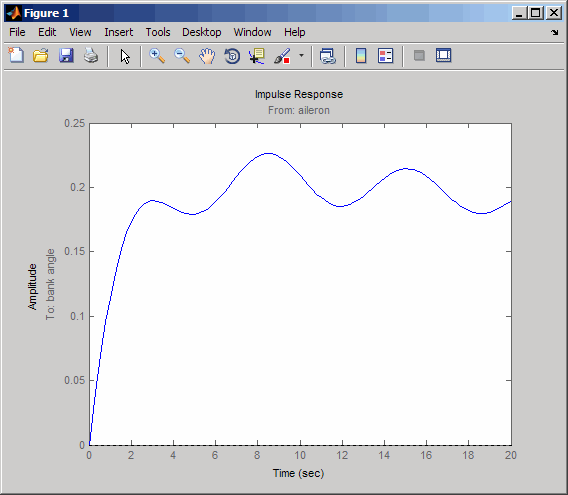
ジェット機は、非ゼロバンク角近傍で振動しています。このように、ジェット機は補助翼へのインパルス入力に応答して方向を変えています。この挙動の重要性は、このケース スタディの後半で説明します。
一般に、ヨー ダンパーは測定出力としてヨー レートを、また制御入力として方向舵を使用して設計されます。対応する周波数応答を確認します。
sys11=sys('yaw','rudder') % Select I/O pair.
bode(sys11)

このボード線図から、方向舵にはやや減衰したダッチ ロール モード近傍 (つまり、ω = 1 ラジアン/秒の近傍) で大きな影響があることが確認できます。
根軌跡の設計
合理的な設計の目的は、固有振動数 ωn < 1.0 ラジアン/秒で、減衰率 ζ > 0.35 を与えることです。最も簡単な補償器は静的ゲインなので、まず根軌跡法を使用して適切なゲインの値を決定します。
% Plot the root locus for the rudder to yaw channel rlocus(sys11)
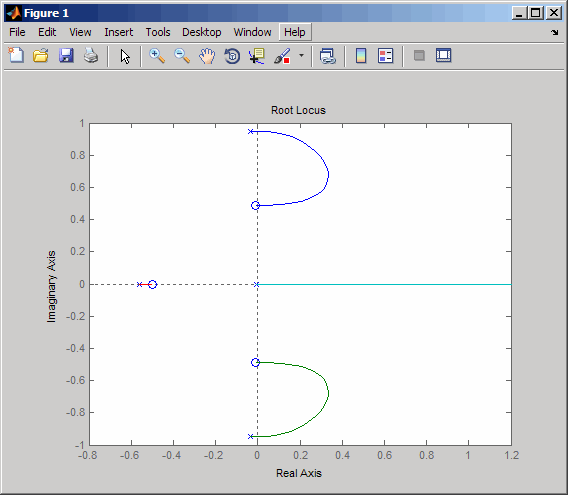
これは、負のフィードバックに対する根軌跡で、システムがほぼ瞬間的に不安定になることを示しています。その代わりに、正のフィードバックを使用すると、システムの安定性を維持できる場合があります。
rlocus(-sys11) sgrid
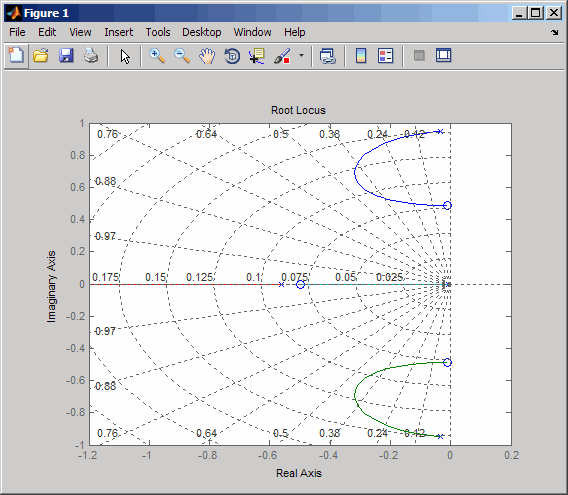
このほうが適切です。単純なフィードバックを使用すると、ζ > 0.45 の減衰率を達成できます。青色の曲線をクリックし、データ マーカーを移動して、ゲインと減衰率を追跡します。0.45 の減衰率に到達するには、ゲインは約 2.85 となる必要があります。次の図は、よく似た値のデータ マーカーを示します。

次に、SISO フィードバック ループを閉じます。
K = 2.85;
cl11 = feedback(sys11,-K); % Note: feedback assumes negative
% feedback by default
20 秒間の閉ループ インパルス応答をプロットし、開ループ インパルス応答と比較します。
impulse(sys11,'b--',cl11,'r',20)
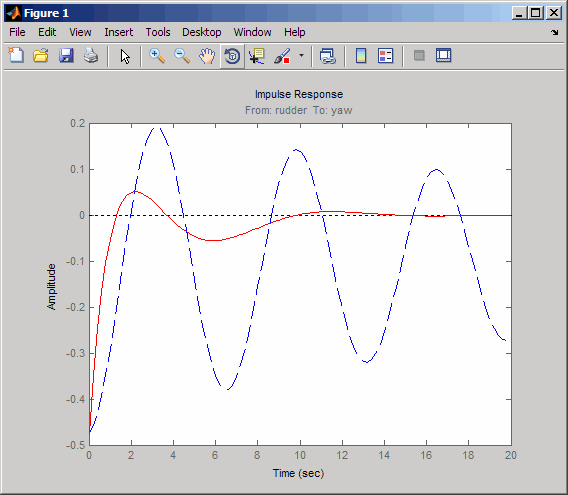
閉ループ応答は、直ちに安定し、特に開ループ応答と比較するとあまり振動しないことがわかります。
ここで、完全な MIMO モデルのループを閉じて、補助翼からの応答がどのようになるかを確認します。フィードバック ループには、プラントの入力 1 と出力 1 が含まれます (この入力/出力の組み合わせを選択するインデックス ベクトルを入力引数として関数 feedback を使用します)。MATLAB® プロンプトで次のように入力します。
cloop = feedback(sys,-K,1,1);
damp(cloop) % closed-loop poles
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-3.42e-01 1.00e+00 3.42e-01 2.92e+00
-2.97e-01 + 6.06e-01i 4.40e-01 6.75e-01 3.36e+00
-2.97e-01 - 6.06e-01i 4.40e-01 6.75e-01 3.36e+00
-1.05e+00 1.00e+00 1.05e+00 9.50e-01 MIMO インパルス応答をプロットします。
impulse(sys,'b--',cloop,'r',20)
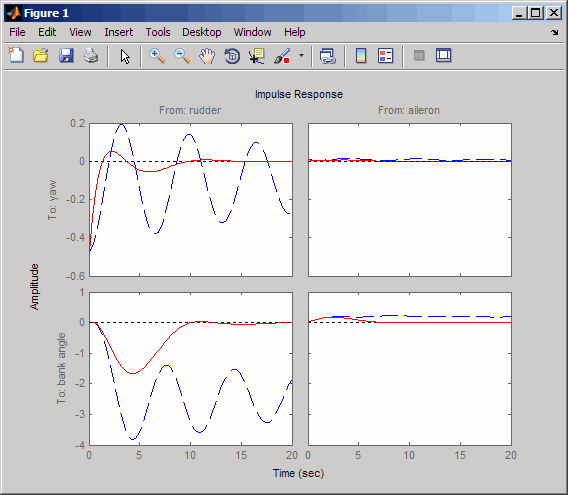
ヨー レート応答は減衰されていますが、補助翼 (入力 2) からバンク角 (出力 2) へのプロットを確認します。補助翼を移動すると、システムでは通常の航空機のようなバンクが行われません。これは、スパイラル モードを過度に安定化したことになります。通常は、スパイラル モードは非常に遅いので、補助翼を操作し続けなくても、機体をバンクしながら旋回できます。パイロットはこのような操作に慣れているため、通常どおりに操縦できなくなるような前述の設計は好まれません。そこで、スパイラル モードを高周波数側に移動することにします。
ウォッシュアウト フィルター設計
ここで、必要なことは、ループを閉じたときにスパイラル モードが左半面において、より左側に移らないようにすることです。飛行制御設計者がこの問題に対処できる 1 つの方法は、以下のようなウォッシュアウト フィルター kH (s) を使用することです。
ウォッシュアウト フィルターは、原点に零点を配置するため、スパイラル モードの極は、原点近傍に限定されます。時定数を 5 秒とするために α = 0.2 とし、根軌跡法を使用してフィルター ゲイン H を決定します。まず、以下により、ウォッシュアウトの固定部分 s/(s + α) を指定します。
H = zpk(0,-0.2,1);
ウォッシュアウトを設計モデル sys11 (入力 1 と出力 1 の関係) と直列に接続して、次の開ループ モデルを取得します。
oloop = H * sys11;
また、この開ループ モデルに対して、次のような根軌跡を描きます。
rlocus(-oloop) sgrid
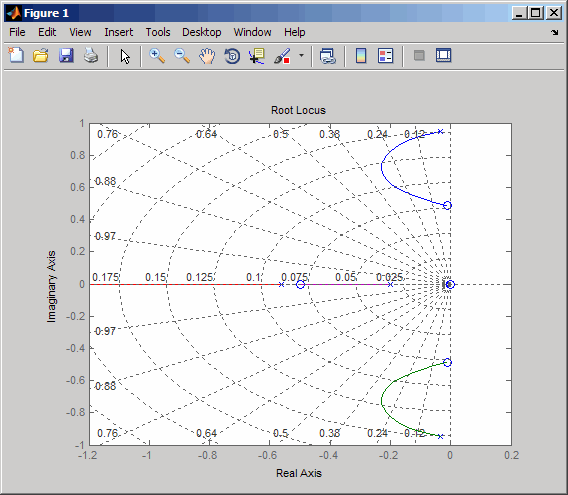
上側の曲線の近くにデータ マーカーを作成し、ドラッグして最大減衰比が約 ζ = 0.3 になる位置を見つけます。
次の図は、最大減衰比のデータ マーカーを示します。ゲインは約 2.07 です。
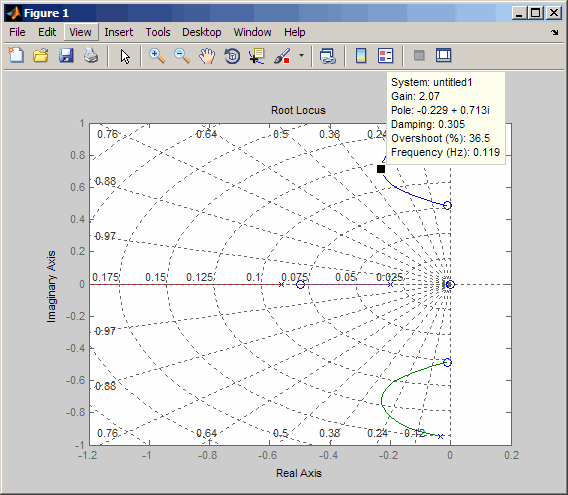
方向舵からヨー レートへの閉ループ応答を確認します。
K = 2.07; cl11 = feedback(oloop,-K); impulse(cl11,20)
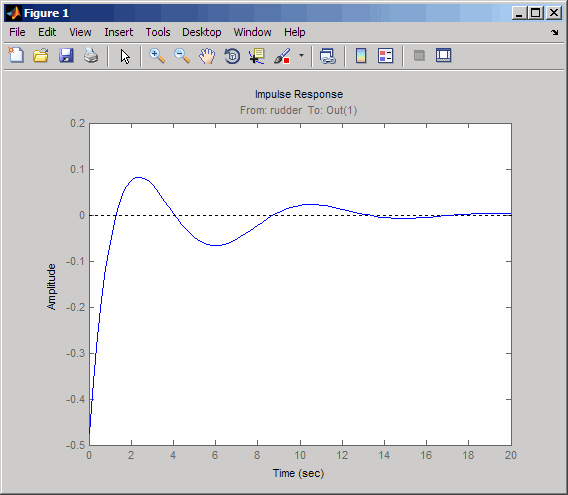
この応答はほど良く整定しますが、前の設計に比べて減衰が小さくなります。最後に、ウォッシュアウト フィルターによってスパイラル モードの問題が解決したかどうかを確認できます。まず、次のように完全なウォッシュアウト フィルター kH (s) (ウォッシュアウト + ゲイン) を構成します。
WOF = -K * H;
次に、MIMO モデル sys の最初の I/O の組み合わせに関して、ループを閉じ、インパルス応答をシミュレーションします。
cloop = feedback(sys,WOF,1,1); % Final closed-loop impulse response impulse(sys,'b--',cloop,'r',20)
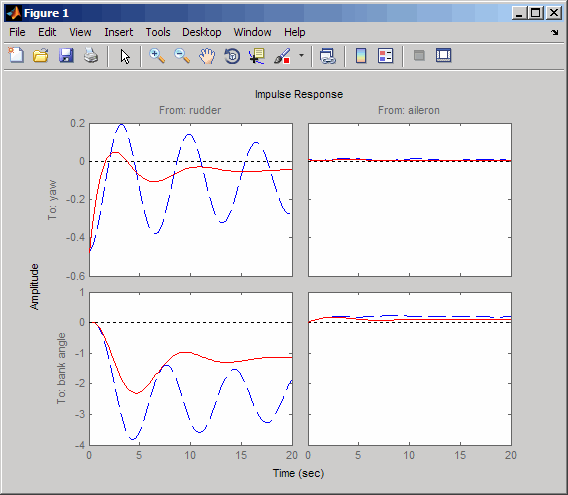
補助翼インパルス (入力 2) によるバンク角応答 (出力 2) は、この短い時間枠で、仕様をほぼ満たす定常特性を示すようになりました。応答をより詳しく調べるには、右クリック メニューで [I/O セレクター] を使用して (2,2) I/O の組み合わせを選択してください。
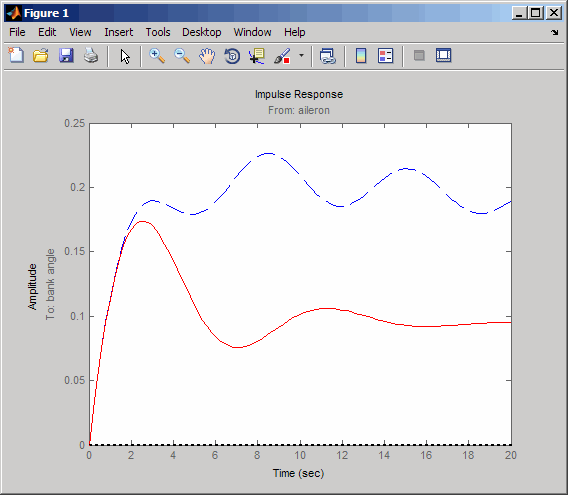
減衰仕様を完全には満たしていませんが、この設計はシステムの減衰を実質的に大きくし、これでパイロットは飛行機を通常どおりに操縦できます。