コマンドラインでの平衡化打ち切りによるモデルの近似

この例では、MATLAB® コマンドラインでモデルの低次元化近似を計算する方法を説明します。

平衡化打ち切りは、モデルの動作全体に対するエネルギーの寄与が最も少ない状態を削除します。そのため、最初にモデルの各状態のエネルギー寄与を調べます。モデルの動作全体に大きく寄与する状態の数に基づいて近似次数を選択します。

この例では、高次のモデルを読み込みます。hplant は 23 次の SISO モデルです。

load ltiexamples hplant
order(hplant)

ans = 23

reducespec を使用してモデル次数の低次元化タスクを作成します。

R = reducespec(hplant,"balanced");

ハンケル特異値 (HSV) プロットを使用して、hplant での状態ごとのエネルギーの相対量を調べます。

view(R)

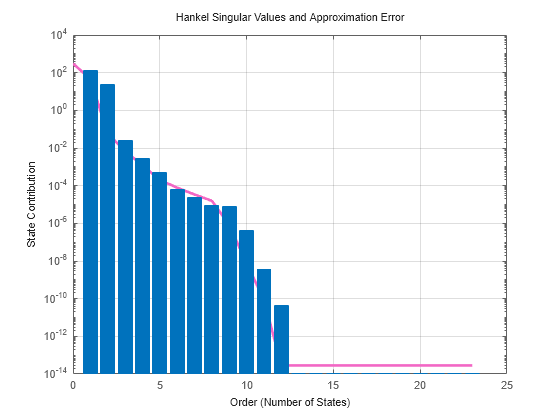
ハンケル特異値が小さいことは、関連する状態がシステムの動作にほとんど影響しないことを示します。このプロットから、2 つの状態がシステムのエネルギーで最も考慮されていることがわかります。そのため、getrom を使用してモデルを 1 次または 2 次に低次元化してみます。

hplant1 = getrom(R,Order=1,Method="Truncate");
hplant2 = getrom(R,Order=2,Method="Truncate");

getrom への 2 番目の引数は、hplant1 が hplant の 1 次近似で、hplant2 が 2 次近似となるようにターゲットの近似次数を指定します。既定では、getrom は最も小さいハンケル特異値をもつ状態を破棄し、残りの状態をシステムの DC ゲインを保持するように変更します。Method オプションを "Truncate" に設定すると、getrom は残りの状態を変更せずに低エネルギーの状態を破棄します。

低次元化されたモデルで作業をする場合、近似を行うことで、アプリケーションにとって重要な周波数に誤差が導入されることがないように確認することが大切です。したがって、元のシステムと近似したシステムの周波数応答を比較します。MIMO システムの場合、sigmaplot コマンドを使用します。SISO システムの場合、ボード線図を調べます。

bodeplot(hplant,hplant2,hplant1)
legend('Original','2nd order','1st order')

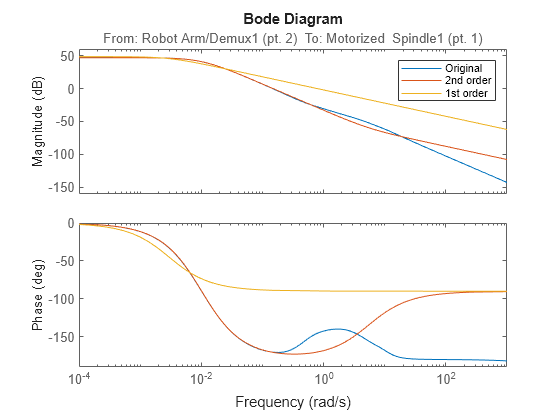
低い周波数では特に、2 次近似 hplant2 が元の 23 次システムと非常によく一致します。1 次システムはあまり一致しません。

一般的に、近似したモデルの次数を減らすと、近似したモデルの周波数応答と元のモデルの周波数応答との間に相違が生じ始めます。重要な帯域での精度が十分に高い近似を選択してください。たとえば制御システムの場合、制御帯域幅内で高い精度を保とうとすることがあります。制御帯域幅を大きく超え、ゲインが迅速にロールオフするような帯域幅での周波数精度は、それほど重要ではないでしょう。

時間領域における近似を確認することもできます。たとえば、元のシステムと低次元化されたシステムのステップ応答を調べます。

stepplot(hplant,hplant2,'r--',hplant1,'g--')
legend('Original','2nd order','1st order','Location','SouthEast')

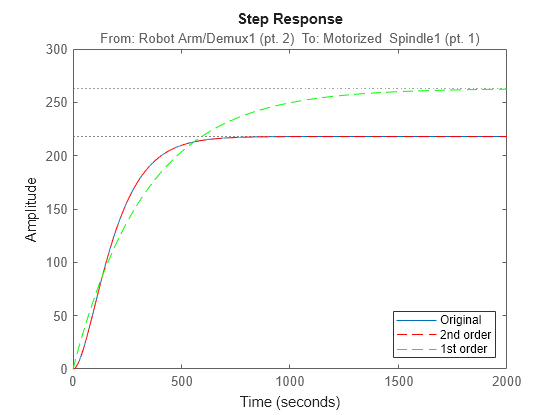
この結果から、2 次近似が元の 23 次システムにとって適切であることが確認されます。

コマンドラインでの平衡化打ち切りによるモデルの近似

参考

関数

ライブエディタータスク

関連するトピック

コマンド ラインでの平衡化打ち切りによるモデルの近似

参考

関数

ライブ エディター タスク

関連するトピック

コマンドラインでの平衡化打ち切りによるモデルの近似

ライブエディタータスク