量子化されたシステムの絶対的な安定性

この例では次を使用します。

スクリプトを開く

この例では、線形時不変システムが円錐セクターに属する静的な非線形性とのフィードバック相互接続にある場合、絶対的な安定性を強制する方法を示します。

フィードバック接続

図 1 に示すフィードバック接続について考えます。

図 1: フィードバック接続

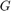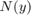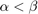$G$ は線形時不変システム、 $N(y)$ は次を満たす円錐セクター $[\alpha,\beta]$ (ここで $\alpha<\beta$ ) に属する静的な非線形性です。

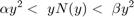
$\alpha y^2<~yN(y)<~\beta y^2$

この例では、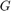 $G$ は次の離散時間システムです。

A = [0.9995, 0.0100, 0.0001;
    -0.0020, 0.9995, 0.0106;
          0,      0, 0.9978];
B = [0, 0.002, 0.04]';
C = [2.3948, 0.3303, 2.2726];
D = 0;
G = ss(A,B,C,D,0.01);

セクター境界のある非線形性

この例では、非線形性 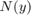$N(y)$ が対数量子化器となります。これは次のように定義されます。

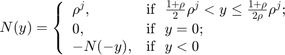
$N(y) = \left\{ \begin{array}{ll} \rho^j, & \mbox{if~ $
\frac{1+\rho}{2}\rho^j < y \leq \frac{1+\rho}{2\rho}\rho^j$};\\0, &
\mbox{if ~$y = 0$}; \\ -N(-y), & \mbox{if~ $y < 0$} \end{array} \right.
$

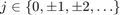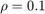ここで、 $j\in \{0,\pm1,\pm2,\dots \}$ です。この量子化器はセクター境界 $[\frac{2\rho}{1+\rho},\frac{2}{1+\rho}]$ に属します。たとえば、 $\rho = 0.1$ の場合、量子化器は円錐セクター [0.1818,1.8182] に属します。

% Quantizer parameter
rho = 0.1;
% Lower bound
alpha = 2*rho/(1+rho)
% Upper bound
beta = 2/(1+rho)

alpha =

    0.1818


beta =

    1.8182

量子化器のセクター境界をプロットします。

PlotSectorBound(rho)

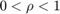$\rho$ は量子化の密度を表します。ここで $0<\rho<1$ です。 $\rho$ が大きいほど、量子化された値はより正確になります。この量子化器の詳細については、[1] を参照してください。

絶対的な安定性の円錐セクター条件

量子化器の円錐セクター行列は次によって与えられます。

$Q = \left(\begin{array}{cc} 1 & -\frac{\alpha+\beta}{2} \\
-\frac{\alpha+\beta}{2} & \alpha\beta \end{array}\right).$

図 1 のフィードバック接続の安定性を保証するには、線形システム 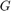$G$ が次を満たす必要があります。

$\int_0^T \left(\begin{array}{c} u(t)\\-y(t)\end {array} \right)^T Q
\left(\begin{array}{c} u(t)\\-y(t)\end {array} \right) > 0$

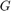ここで、 $u$ と $y$ は、それぞれ $G$ の入力と出力です。

この条件は、セクターインデックス $R$ が 1 より小さいかどうかを確認することで検証できます。

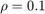$\rho = 0.1$ である量子化器の円錐セクター行列を定義します。

Q = [1,-(alpha+beta)/2;-(alpha+beta)/2,alpha*beta];

Q と G のセクターインデックスを取得します。

R = getSectorIndex([1;-G],-Q)

R =

    1.8247

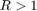$R>1$ であるため、閉ループシステムは安定していません。この不安定性を確認するには、次の Simulink® モデルを使用します。

mdl = 'DTQuantization';
open_system(mdl)

Simulink モデルを実行します。

sim(mdl)
open_system('DTQuantization/output')

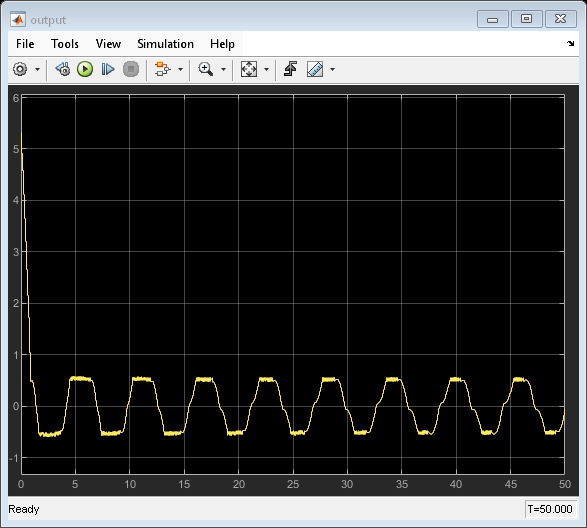
出力軌跡から、閉ループシステムが不安定であることがわかります。これは、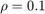 $\rho = 0.1$ の量子化器では粗すぎるためです。

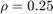$\rho = 0.25$ として、量子化の密度を濃くします。量子化器は円錐セクター [0.4,1.6] に属します。

% Quantizer parameter
rho = 0.25;
% Lower bound
alpha = 2*rho/(1+rho)
% Upper bound
beta = 2/(1+rho)

alpha =

    0.4000


beta =

    1.6000

量子化器のセクター境界をプロットします。

PlotSectorBound(rho)

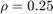$\rho = 0.25$ である量子化器の円錐セクター行列を定義します。

Q = [1,-(alpha+beta)/2;-(alpha+beta)/2,alpha*beta];

Q と G のセクターインデックスを取得します。

R = getSectorIndex([1;-G],-Q)

R =

    0.9702

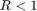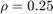$R<1$ なので、 $\rho = 0.25$ である量子化器は、フィードバック接続の安定性の円錐セクター条件を満たします。

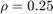$\rho = 0.25$ として Simulink モデルを実行します。

sim(mdl)
open_system('DTQuantization/output')

セクターインデックスに示されるように、閉ループシステムは安定しています。

参考文献

[1] M. Fu and L. Xie,"The sector bound approach to quantized feedback control," IEEE Transactions on Automatic Control 50(11), 2005, 1698-1711.