モデル次数の低次元化

モデル次数の低次元化のコマンド

次の表に示すコマンドを使用して、低次元化された SISO モデルや MIMO モデルを作成できます。

モデル次数の低次元化のコマンド

 
hsvd

LTI モデルのハンケル特異値の計算

balred

低次元化されたモデル近似

minreal

最小実現 (極/零相殺)

balreal

入力/出力の平衡化実現の計算

modred

I/O 平衡実現での状態の削除

sminreal

構造的な最小実現

モデル次数の低次元化の方法

モデルの次数を低次元化するために、以下のような方法があります。

  • 関数 sminreal を使用して、入力や出力に構造的に接続されていない状態をモデルから消去します。

    構造的に接続されていない状態を消去する際には数値計算を行わないため簡単であり、モデルの低次元化における最初のステップとして良い方法です。

  • balred を使用してモデルの低次の近似を計算します。

  • minreal を使用して相殺する極/零点のペアを除去します。

例: 気化装置モデル

この例では、固体を気体に変換する装置である気化装置モデルを示します。元のモデルは非線形です。

モデルの読み込み

線形化されたモデルを読み込むには、MATLAB プロンプトで次のように入力します。

load ltiexamples

MATLAB® において気化装置の例は、変数 gasf に格納されています。次のように入力します。

size(gasf)

これで以下が出力されます。

4 出力、6 入力、25 の状態をもつ状態空間モデル。

SISO モデル次数の低次元化

MIMO モデル次数の低次元化に述べるように、完全な MIMO モデルの低次元化を試みる前に、1 組の I/O の次数を低次元化し、モデルを低次元化するツールの動作方法を確認します。

この例では、気化装置の 1 組の入力/出力 (入力 5 から出力 3) を取り扱います。

sys35 = gasf(3,5);

モデルを低次元化する前に、次のように入力して、極と零点の位置を調べます。

pzmap(sys35)

ズーム機能を使用するか、次のように入力して、結果の原点付近をズーム インします。

axis([-0.2 0.05 -0.2 0.2])

次の図に結果を示します。

気化装置の極-零点配置図 (ズーム イン)

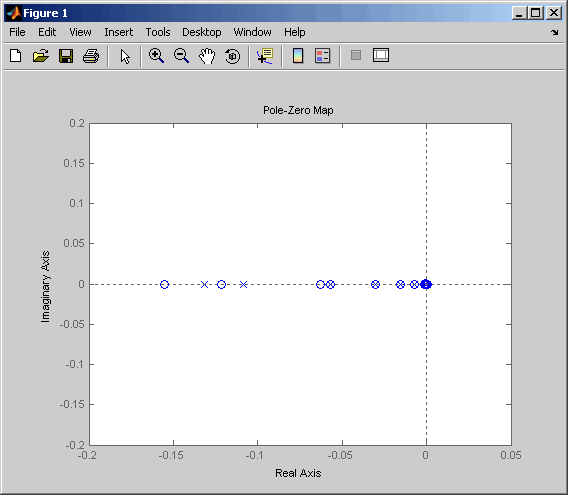
モデルはほぼ極-零点相殺を示しているので、モデル次数の低次元化の候補となります。

この SISO モデルの低次元化を見つけるには、次の手順に従います。

  1. ハンケル特異値 (HSV) プロットを使用して、状態ごとのエネルギーの相対量を調べることによって、低次元化されたシステムに対する適切な次数を選択します。次のコマンドを入力して、

    hsvd(sys35)
    これで HSV プロットを作成します。

    右クリック メニューを使用して対数スケールに変更すると、次のようになります。

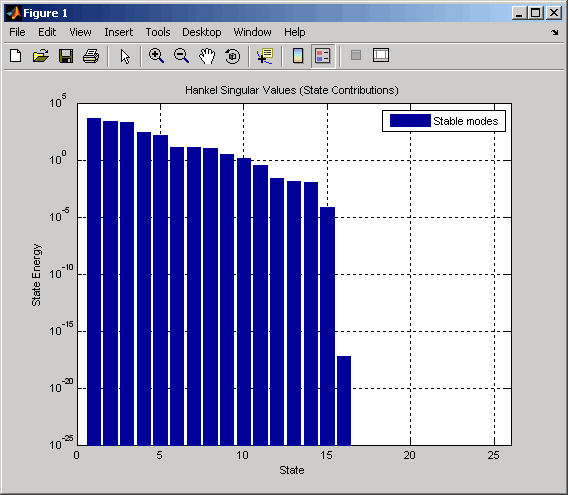
    ハンケル特異値が小さいことは、関連する状態が I/O の動作にほとんど影響しないことを示します。このプロットは、最後の 10 個の状態 (10 個の最小のハンケル特異値) を削除しても、近似誤差にほとんど影響しないことを示します。

  2. 最後の 10 個の状態を削除し、15 次の近似を作成するには、次のように入力します。

    rsys35 = balred(sys35,15);
    「size(rsys35)」と入力すると、低次元化されたシステムが状態を 15 個のみ含むことがわかります。

  3. 元の次数と低次元化されたモデルのボード応答を、bode コマンドを使用して比較します。

    bode(sys35,'b',rsys35,'r--')
    次の図は結果を示しています。

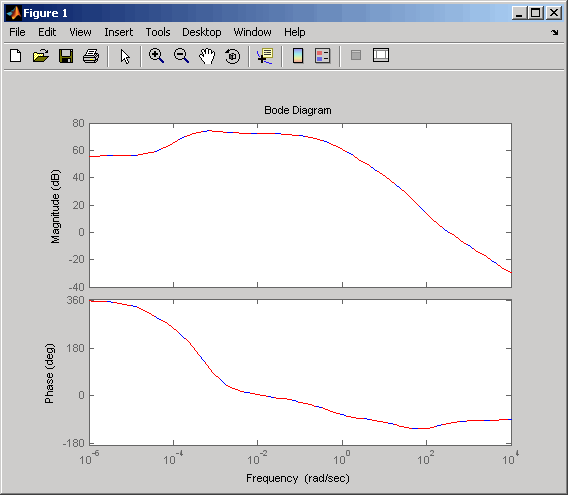
    図の曲線が重なることから、低次元化されたモデルは元のシステムの良い近似であることがわかります。

この手順を繰り返して状態を削除していくと、モデルの次数をさらに減らせます。gasf モデルの次数を一度に 5 次、10 次、15 次に減らすには、次のコマンドを入力します。

rsys35 = balred(sys35,[5 10 15]);
これらの 3 つの低次元化されたシステムと元の次数のシステムのボード線図をプロットするには、次のように入力します。
bode(sys35,'b',rsys35,'r--')

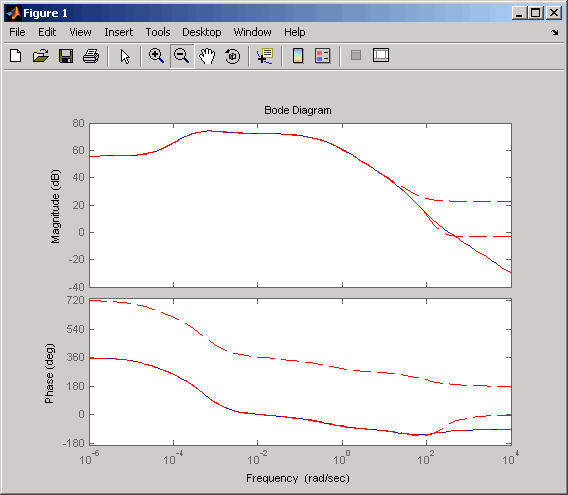
次数が減少するにつれて、誤差が増加する様子が確認できます。

MIMO モデル次数の低次元化

以下のように、SISO モデルと同じステップを使用して、MIMO モデルを近似できます。

  1. ハンケル特異値 (HSV) プロットを使用して、状態ごとのエネルギーの相対量を調べることによって、低次元化されたシステムに対する適切な次数を選択します。

    次のように入力します。

    hsvd(gasf)
    これで HSV プロットを作成します。

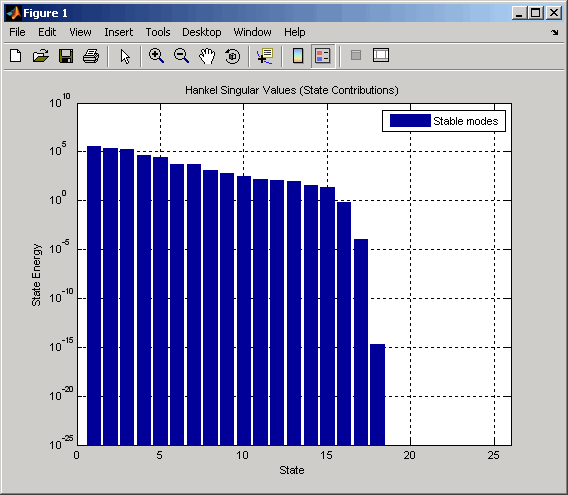
    最後の 8 個の状態 (最小の 8 個のハンケル特異値と関連) を削除しても、結果の 17 次のシステムにおける誤差にほとんど影響しないはずです。

  2. 最後の 8 個の状態を削除し、17 次の MIMO システムを作成するには、次のように入力します。

    rsys=balred(gasf,17);
    「size(gasf)」と入力すると、低次元化されたシステムが状態を 17 個のみ含むことがわかります。

  3. 近似誤差を視覚的に検証しやすくするために、MIMO ボード線図ではなく特異値プロットを使用します。次のように入力します。

    sigma(gasf,'b',gasf-rsys,'r')
    これで、元のシステムを低次元化の誤差と比較するために、特異値プロットを作成します。

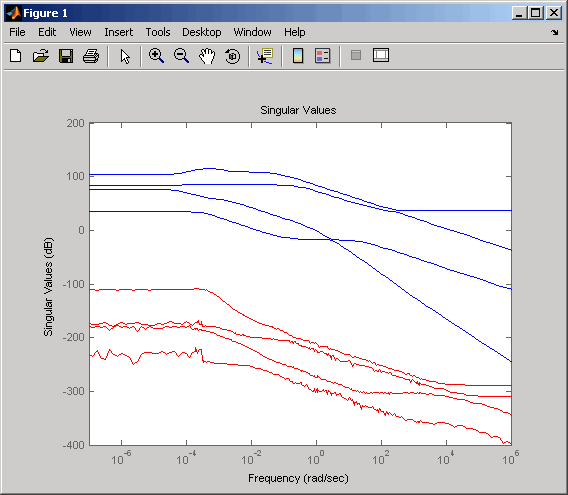
    低次元化による誤差は元のシステムに比べて小さく、低次元化モデルは元のモデルの良い近似になっています。

謝辞

MathWorks® は、この例にて気化装置モデルの使用を承諾いただいた ALSTOM® Power UK に感謝いたします。このモデルは、ALSTOM Benchmark Challenge on Gasifier Control の一部として発表されました。詳細については、Dixon, R., (1999), "Advanced Gasifier Control," Computing & Control Engineering Journal, IEE, Vol. 10, No. 3 の 92 ～ 96 ページを参照してください。