OTFS 変調

R2024a 以降

この例では、直交時間周波数空間 (OTFS) 変調を使用する通信リンクをシミュレートするとともに、そのキャリア間干渉 (ICI) キャンセル機能について、標準の直交周波数分割多重 (OFDM) 変調と比較しながら説明します。OTFS は、高ドップラー マルチパスで構成されるチャネル環境において耐性のあるマルチキャリア変調方式です [1]。現代の無線システムのほとんどは OFDM を使用しており、ICI をキャンセルできないため、高ドップラー チャネルでは問題が発生します。この例では、単純な OTFS 送受信機を実装し、移動散乱体を含むチャネルを介してデータをフィルター処理し、推定されたチャネル パラメーターを使用して遅延-ドップラー (DD) 領域でチャネルをイコライズし、送信されたコードワードを検出します。

OTFS の目的

高ドップラー チャネルでは、チャネル特性が急速に変化するため、チャネルのコヒーレンス時間が低下します。コヒーレンス時間はチャネル係数の変動に反比例します。OFDM は長年にわたり、さまざまな無線システムで選択される変調スキームでした。OFDM を使用する場合、高ドップラー チャネル環境では頻繁なチャネル測定が必要となり、ICI が発生します。高ドップラー チャネル環境における OFDM の 2 つの欠点として、より頻繁なチャネル測定が必要になることと ICI の発生が挙げられます。

• OFDM は時間-周波数 (TF) 領域でデータを送信し、各データ シンボルはそれぞれ独立した直交周波数サブキャリアにあります。参照 (パイロット) シンボルはチャネル測定を可能にしますが、伝送帯域幅の一部を占有します。チャネル特性が急速に変化するため、パイロットを頻繁に送信しなければなりません。これらのパイロットはデータを置き換え、結果としてスループットを低下させます。

• OFDM は、散乱体の相対速度の違いにより個々のパスに異なる周波数オフセットが生じる高ドップラー マルチパス チャネルにおいて、ICI の影響を受けます。異なるパスからの周波数シフトにより、干渉のないシンボル検出に必要な周波数領域の直交性が損なわれます。

OTFS 変調では、遅延-ドップラー領域でデータを送信するため、チャネルを頻繁に測定する必要がなくなります。この領域は、受信機に対する遅延 (伝送遅延) と速度 (ドップラー シフト) を伴う移動散乱体を表します。散乱体の数が限られていると仮定すると、散乱体のチャネル表現はスパース行列になります (遅延領域チャネル行列は、散乱体を表すいくつかの非ゼロのエントリを除いて、ほとんどゼロになります)。効率的なチャネル推定とイコライゼーションの手法では、このスパース性を活用します。さらに、散乱体が一定の速度を維持する場合、チャネルは DD 領域内で準定常になります。パイロットの送信の必要性が減少し、有効なスループットが増加します。

OTFS は、高ドップラー チャネルに対する耐性があるため、5G NR [2] の変調候補として検討されており、高速ユース ケースの新しい要件を満たす 6G [3] の変調候補としても検討されています。

OTFS データ グリッド

OTFS 変調では、情報シンボルは、遅延-ドップラー領域を表す $$M$$ 行 $$N$$ 列の 2 次元送信データ グリッド $$X_{dd}[k,l]$$ にマッピングされます。ここで、$$k$$ は遅延軸インデックス $$k=0,1,...,M-1$$ であり、$$l$$ はドップラー軸インデックス $$l=0,1,...,N-1$$ です。このグリッドは 1 つの OTFS シンボルであり、グリッド内の各列はサブシンボルです。インデックス $$k$$ とインデックス $$l$$ は、遅延 = $$k/(M*df)$$ およびドップラー = $$l/(N*T)$$ の関係によって実際の遅延とドップラー シフトに関連付けられます。ここで、$$df$$ はヘルツ単位のサブキャリア間隔であり、$$T$$ は任意のサイクリック プレフィックスを含む OTFS サブシンボルの秒単位の持続時間です。インデックス $$k$$ とインデックス $$l$$ は、正規化された遅延と正規化されたドップラー シフトです。

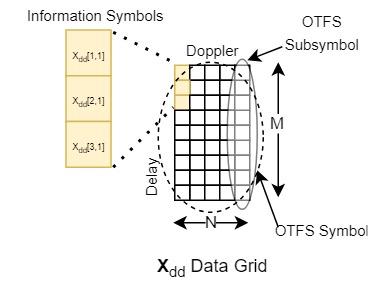
遅延-ドップラー領域

遅延-ドップラー領域での演算は、パルス ドップラー レーダー信号処理におけるレーダー反射の処理に似ています。レーダーは狭帯域パルスを放射し、返されたエコーを、返された信号の到着時間 (送信と受信の間の遅延によって測定) に基づいてレンジに、ドップラー シフト エコーに基づいて速度に分類します。同様に、送信機はレーダー エコーのようなマルチパス反射によって受信機に信号を送信する場合があります。それぞれのマルチパス反射では、送信機に対する相対的な遅延と、受信機に対する反射体の相対的な動きによるドップラー シフトが生じる可能性があります。

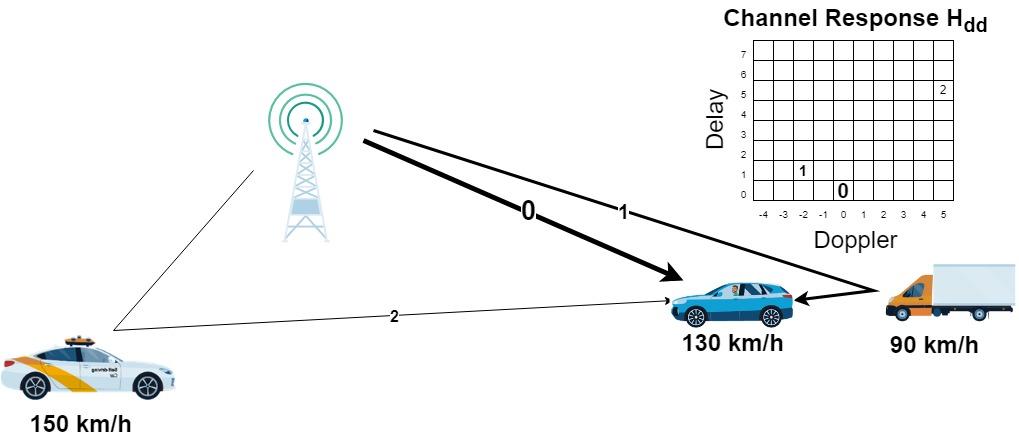
下の図では、走行中の乗用車内に設置された受信機に基地局が信号を送信しています。右上に表示された 2 次元遅延-ドップラー チャネル応答 $$H_{dd}$$ には、個々のパスがそれぞれのパス番号で示されています。数字の大きさとパスの太さは、パスの強度に比例しています。

直接見通し線は基準時間であり、遅延 0 サンプルの位置に太線で示されています。乗用車は 130 km/h で基地局に向かって移動していますが、乗用車内の受信機が搬送波周波数を調整してドップラー シフトの影響を補正するため、パスのドップラー シフト インデックスは 0 になります。パス 1 は、受信側の乗用車よりも遅い、近くのトラックからの反射を示しています。パス 1 では、信号の移動距離が長いため伝送遅延がわずかに長くなり、乗用車がトラックからゆっくりと離れていくため、ドップラー シフトが負の値になります。パス 2 は、より遠方を乗用車に向かって走行するパトカーからの別の反射であるため、ドップラーの値は正になり、遅延はより長く、パス ゲインは小さくなります。

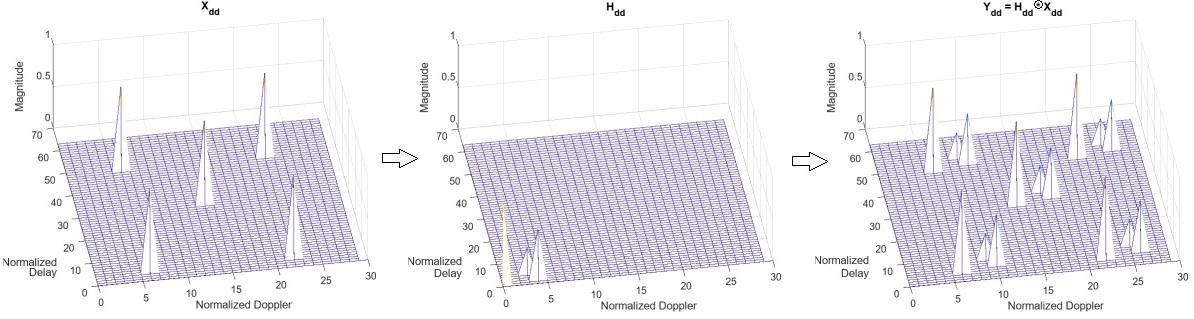
単一の DD グリッド要素に対するマルチパスの影響を以下に示します。$$X_{dd}$$ には 5 つの送信信号が含まれ、$$H_{dd}$$ はチャネル応答です。$$Y_{dd}$$ は、$$X_{dd}$$ と $$H_{dd}$$ の 2 次元畳み込みです。OTFS では、時間制限のあるシグナリングは畳み込みが循環的であり、位相回転が含まれることを意味します。これは "ねじれ畳み込み" として知られています。

遅延-ドップラー領域から時間-周波数領域への表現

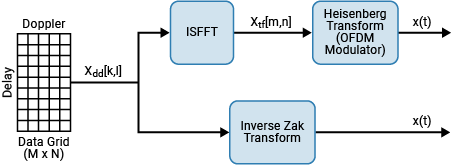
遅延-ドップラー領域が時間-周波数領域にどのように変換されるかを理解するために、そのプロセスを OFDM に関連付けることができます。以下の図は、プリコードされた OFDM 変調/復調システムとしての OTFS 変調と OTFS 復調を示しています。$$M$$ は OFDM シンボル内のサブキャリアの数と等価であり、$$N$$ は 1 つのフレームに含まれる OFDM シンボルの数と等価です。

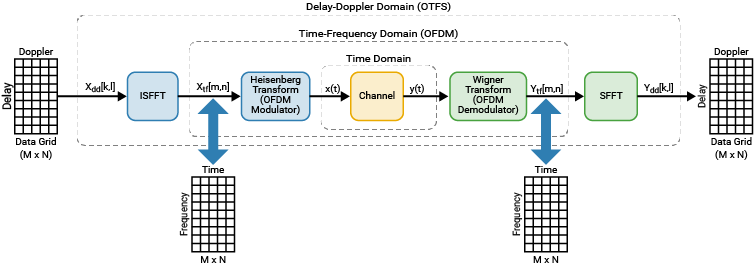
図の内部セクションには、OFDM 変調器、チャネル、および OFDM 復調器から成る一般的な OFDM 処理チェーンが示されています。Heisenberg 変換と Wigner 変換は、それぞれ OFDM 変調器と OFDM 復調器の一般化です。

まず、逆シンプレクティック有限フーリエ変換 (ISFFT) [1] は、変調されたシンボルを遅延-ドップラー領域 $$X_{dd}$$ から時間-周波数領域 $$X_{tf}$$ に変換します。

$$X_{tf}[m,n]=\frac{1}{MN}\sum _{l=0}^{M-1}\sum _{k=0}^{N-1}{X}_{dd}[k,l]e^{j2\pi (\frac{nk}{N}-\frac{ml}{M})}.$$

内側の総和項は、ドップラー軸上の $$X_{dd}$$ の逆離散フーリエ変換 (IDFT) です。

$$\frac{1}{MN}\sum _{k=0}^{N-1}{X}_{dd}[k,l]e^{j\frac{2\pi nk}{N}}=\frac{1}{M}IFFT(X_{dd}^T{)}^T=X_{dt}.$$

この演算は、$$X_{dd}$$ を遅延-ドップラー領域から $$X_{dt}$$ で示される遅延-時間領域に変換します。MATLAB ® では、配列の DFT は各列に対して個別に演算されます。IDFT が $$X_{dd}$$ の転置に適用され、ドップラー軸上で IDFT が演算された後、その結果が転置されて適切な配列次元に戻されます。

ISFFT 式の外側の総和は、遅延軸上の DFT です。

$$\sum _{l=0}^{M-1}{X}_{dt}[m,n]e^{-j\frac{2\pi ml}{M}}=FFT(X_{dt})$$

したがって ISFFT は次に帰着します。

$$X_{tf}[m,n]=\frac{1}{M}FFT(IFFT(X_{dd}^T{)}^T).$$

この時点では、$$X_{tf}[m,n]$$ は、よく知られている時間-周波数領域のデータを表します。Heisenberg 変換は、変換されたシンボル $$X_{tf}$$ を時間領域信号に変換します。

$$x(t)=\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}{X}_{tf}[m,n]g(t-nT)e^{j2\pi m\Delta f(t-nT)}.$$

$$T$$ は 1 つの OFDM シンボルの持続時間です。パルス整形フィルター $$g(t)$$ は、分数ドップラー シフト (ドップラー周波数が $$1/(NT)$$ の倍数にならない場合) によって引き起こされるチャネル拡散を軽減します。フィルターが 0 から $$T$$ に時間制限された箱型ウィンドウである場合、Heisenberg 変換は単に $$X_{tf}$$ の各列に対して演算する OFDM 変調器になります。OTFS 変調は 2 次元プリコーディング OFDM 変調に帰着します。ここで、プリコーディング演算は ISFFT です。ISFFT は、ドップラー次元に沿って演算を行い、それを時間次元に変換する IDFT であるとともに、遅延次元に沿って演算を行い、それを周波数次元に変換する DFT です。Heisenberg 変換は周波数次元 [2] に沿って演算を行う IDFT であり、これは OFDM 変調と等価です。

逆 Zak 変換

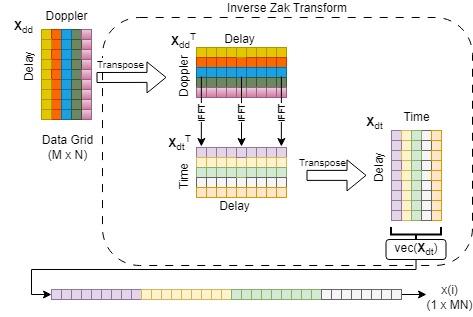
ISFFT と Heisenberg 変換の組み合わせは、逆 Zak 変換 [4] を使用して数学的に表現することもできます。ISFFT と Heisenberg 変換を組み合わせることで IDFT-DFT ペアを排除し、演算をドップラー軸方向の IDFT のみに簡素化します。

矩形パルス整形により、Heisenberg 変換が通常の OFDM 変調器に変換され、それが $$X_{tf}$$ 内の各列に対する単純な IFFT になることを思い出してください。そして、$$X_{tf}$$ の IFFT は次のようになります。

$$X_{dt}=IFFT(X_{tf})=IFFT(\frac{1}{M}FFT(IFFT(X_{dd}^T{)}^T))$$

ここで、$$X_{dt}$$ は入力データの遅延-時間領域表現です。IFFT-FFT の組み合わせにより各演算が相殺されることに留意すると、中間結果は逆 Zak 変換 $$X_{dt}$$ になります。

$$X_{dt}=\frac{1}{M}IFFT(X_{dd}^T{)}^T.$$

この結果は、前に ISFFT と Heisenberg 変換の組み合わせで導出した結果と同じです。逆 Zak 変換は、$$X_{dt}[m,n]$$ のベクトル化された表現から、離散化された時間領域サンプル $$x(i)$$ を出力します。

$$x(m+nM)=vec(X_{dt}[m,n]).$$

符号間干渉 (ISI) の軽減

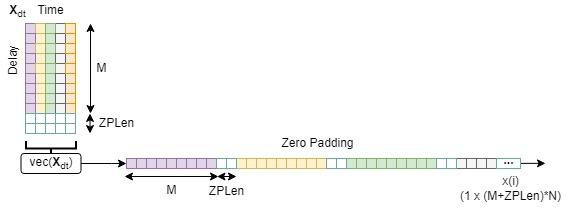
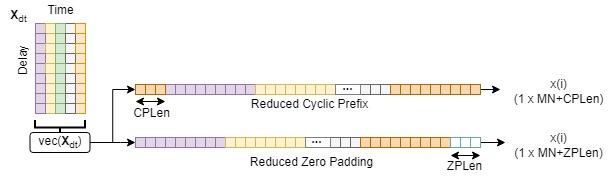
OFDM がサイクリック プレフィックスを使用する方法と同様に、OTFS サブシンボルまたはシンボル間にサイクリック プレフィックスまたはゼロのシーケンスを挿入して ISI を防止します [4]。ゼロ パディング (ZP) は、各 OTFS サブシンボルに長さ ZPLen サンプルのゼロを追加する ISI 軽減手法です。

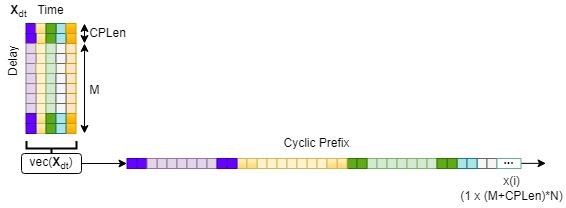
サイクリック プレフィックス (CP) は、各 OTFS サブシンボルの先頭に、それぞれのサブシンボルの最後の CPLen サンプルを付加する手法です。

短縮サイクリック プレフィックス (RCP) は、OTFS シンボルの最後の CPLen サンプルをシンボルの先頭に追加します。短縮ゼロ パディング (RZP) は、OTFS シンボルの末尾に ZPLen 個のゼロを追加します。

高移動度チャネル経由の OTFS のシミュレーション

遅延-ドップラー領域でパイロット信号を送信して、高移動度チャネルをサウンディングし、遅延-ドップラー領域でチャネル応答を観察します。この例では、チャネル サウンディングとデータ伝送を実証するためにゼロ パディングを使用します。

シミュレーションの設定

シミュレーション パラメーターを構成します。基本的な OTFS 概念を示すために、$$M$$ = 64 および $$N$$ = 30 とします。さまざまな変調およびチャネル条件における ISI および ICI の影響を表示するために、SNR を高い値に設定します。

M = 64;          % number of subcarriers
N = 30;          % number of subsymbols/frame
df = 15e3;       % make this the frequency bin spacing of LTE
fc = 5e9;        % carrier frequency in Hz
padLen = 10;     % make this larger than the channel delay spread channel in samples
padType = 'ZP';  % this example requires ZP for ISI mitigation
SNRdB = 40;

チャネル サウンディングのグリッド母集団

サイズが $$M$$ 行 $$N$$ 列の空の配列を作成します。ここで、$$M$$ 行は遅延ビンに対応し、$$N$$ 列はドップラー ビンにマッピングされます。遅延-ドップラー領域のデータが高移動度チャネルを介してどのように伝播するかを示すには、パイロット信号をグリッド位置 (1,16) に配置してチャネルをサウンディングします。他のグリッド要素を空のままにして、受信した遅延-ドップラー グリッドに散乱体のエコーが表示されるようにします。

% Pilot generation and grid population
pilotBin = floor(N/2)+1;
Pdd = zeros(M,N);
Pdd(1,pilotBin) = exp(1i*pi/4); % populate just one bin to see the effect through the channel

OTFS 変調

OTFS 変調を使用し、単一のパイロット シンボルで DD データ グリッドを変調します。helperOTFSmod 関数を使用して、パイロット グリッド Pdd 上で逆 Zak 変換を処理します。

% OTFS modulation
txOut = helperOTFSmod(Pdd,padLen,padType);

高移動度チャネル

固定送信機と移動受信機、および次の異なる遅延とドップラー シフトの移動散乱体を使用して AWGN 高移動度チャネルを作成します。

• 遅延をゼロ、正規化ドップラーをゼロとして、基地局から受信機までの主な伝播パスを表す見通し線パスを作成する。受信機は時間および周波数が基地局と同期されているため、見通し線パスでは遅延もドップラーもゼロになる。

• 受信機から 5 サンプル遅延し、正規化ドップラーの 3 倍のドップラーで受信機から遠ざかる散乱体 1 を作成する。

• 受信機から 8 サンプルを遅延し、正規化ドップラーの 5 倍のドップラーで受信機に向かって移動する散乱体 2 を作成する。

% Configure paths
chanParams.pathDelays      = [0  5   8  ]; % number of samples that path is delayed
chanParams.pathGains       = [1  0.7 0.5]; % complex path gain
chanParams.pathDopplers    = [0 -3   5  ]; % Doppler index as a multiple of fsamp/MN

assert(strcmp(padType,'ZP'),'Example must use ZP pad type');

fsamp = M*df;            % sampling frequency at the Nyquist rate
Meff = M + padLen;       % number of samples per OTFS subsymbol
numSamps = Meff * N;     % number of samples per OTFS symbol
T = ((M+padLen)/(M*df)); % symbol time (seconds)

% Calculate the actual Doppler frequencies from the Doppler indices
chanParams.pathDopplerFreqs = chanParams.pathDopplers * 1/(N*T); % Hz

% Send the OTFS modulated signal through the channel
dopplerOut = dopplerChannel(txOut,fsamp,chanParams);

% Add white Gaussian noise
Es = mean(abs(pskmod(0:3,4,pi/4).^ 2));
n0 = Es/(10^(SNRdB/10));
chOut = awgn(dopplerOut,SNRdB,'measured');

実際の散乱パラメーターの遅延とドップラー シフトの値を表示して、正規化された値を実際の値に接続します。

for k = 1:length(chanParams.pathDelays)
    fprintf('Scatterer %d\n',k);
    fprintf('\tDelay = %5.2f us\n', 1e6*chanParams.pathDelays(k)/(Meff*df));
    fprintf('\tRelative Doppler shift = %5.0f Hz (%5.0f km/h)\n', ...
        chanParams.pathDopplerFreqs(k), (physconst('LightSpeed')*chanParams.pathDopplerFreqs(k)/fc)*(3600/1000));
end

Scatterer 1

	Delay =  0.00 us

	Relative Doppler shift =     0 Hz (    0 km/h)

Scatterer 2

	Delay =  4.50 us

	Relative Doppler shift = -1297 Hz ( -280 km/h)

Scatterer 3

	Delay =  7.21 us

	Relative Doppler shift =  2162 Hz (  467 km/h)

OTFS 復調

復調プロセスを開始するには、受信信号ベクトルを $$M$$ 行 $$N$$ 列の行列 $$Y_{dt}$$ にパックします。Wigner 変換は Heisenberg 変換の逆変換です。この例では矩形パルス整形を使用しているため、Wigner 変換は単純に OFDM 復調演算になります。Wigner 変換に続いて、SFFT は時間-周波数領域グリッドを遅延-ドップラー領域に変換します。

この例では、より効率的な Zak 変換を使用して信号を復調します。

$$Y_{dd}[k,l]=M*FFT(Y_{dt}^T{)}^T.$$

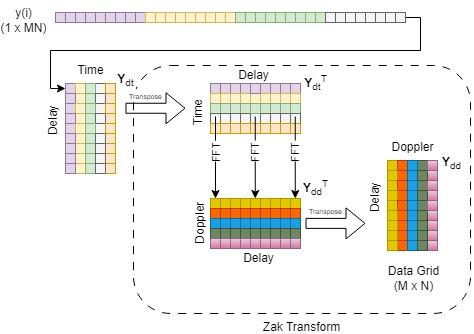
OTFS フレームでサンプルを収集し、遅延-ドップラー領域で信号を復調します。

% Get a sample window
rxIn = chOut(1:numSamps);

% OTFS demodulation
Ydd = helperOTFSdemod(rxIn,M,padLen,0,padType);

遅延-ドップラー チャネル応答

OTFS 復調信号の出力は、(1,16) で送信されたパイロット信号と DD 領域 (5,-10) および (8,6) におけるチャネル表現との畳み込みです。これは OFDM 復調とは異なります。ここで、OFDM 復調信号は、OFDM シンボルと周波数領域チャネル係数のアダマール (要素ごとの) 積です。

線形最小平均二乗誤差 (LMMSE) 推定器は、観測値 $$Y$$ (受信信号) と実際の値 $$P$$ (既知のパイロット信号) の間の平均二乗誤差を最小化する推定方法であり、次で与えられます。

$${\underset{}{\overset{ˆ}{P}}}_{LMMSE}=\frac{Y*P^{*}}{|P{|}^2+{\sigma }_n^2}$$

ここで、$$P^{*}$$ は $$P$$ の複素共役であり、$${\sigma }_n^2$$ はノイズ パワーです。遅延-ドップラー領域でチャネル応答を推定するには、単一のパイロット シンボル $$P_{dd}$$ に対して各グリッド要素 $$Y_{dd}[k,l]$$ で LMMSE を使用し、チャネル応答 $$H_{dd}$$ を計算します。

% LMMSE channel estimate in the delay-Doppler domain
Hdd = Ydd * conj(Pdd(1,pilotBin)) / (abs(Pdd(1,pilotBin))^2 + n0);

受信した DD グリッドをメッシュ プロットで可視化します。

figure;
xa = 0:1:N-1;
ya = 0:1:M-1;
mesh(xa,ya,abs(Hdd));
view([-9.441 62.412]);
title('Delay-Doppler Channel Response H_{dd} from Channel Sounding');
xlabel('Normalized Doppler');
ylabel('Normalized Delay');
zlabel('Magnitude');

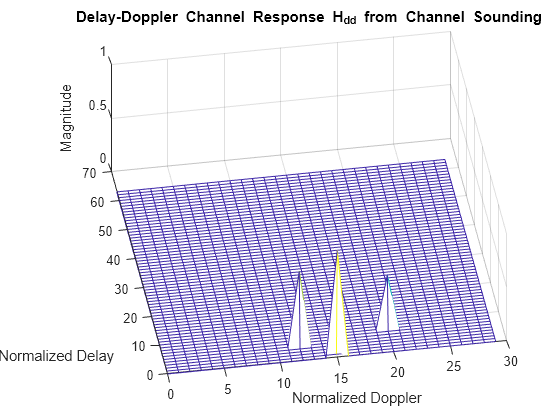
チャネル サウンディングから得られた DD グリッドには、受信機が確認した単一のパイロットからのすべてのパス、各パスの遅延、各パスのドップラー シフト、および各パスの複素数ゲインが表示されます。遅延-ドップラー領域でパイロット シンボルが DD チャネル応答にどのように畳み込まれるかを観察します。パイロットは適切なグリッド位置 (1,16) で正しく受信されます。他の 2 つの散乱体も DD グリッドに表示されます。

• 散乱体 1 はグリッド位置 (1,16) + (5,-3) = (6,13) にある。

• 散乱体 2 はグリッド位置 (1,16) + (8,5) = (9,21) にある。

チャネル推定

遅延-ドップラー領域でのチャネル推定では、チャネル応答内のすべての散乱体のパラメーター (遅延、ドップラー、および複素数ゲイン) を推定する必要があります。チャネル応答 $$H_{dd}$$ から、事前設定されたゲインしきい値を超えるパスを見つけ、一意のパスごとにパラメーターを保存します。同じチャネル経由でデータを送信するときに後で使用するために、チャネル推定値を保存します。

[lp,vp] = find(abs(Hdd) >= 0.05);
chanEst.pathGains = diag(Hdd(lp,vp));   % get path gains
chanEst.pathDelays = lp - 1;            % get delay indices
chanEst.pathDopplers = vp - pilotBin;   % get Doppler indices

高移動度チャネルにおける OFDM と OTFS の比較

OTFS と OFDM はどちらも、サイクリック プレフィックスを通じて ISI の影響を打ち消します。ただし、OFDM 受信機で一般的に使用されるシングルタップ周波数領域イコライザー (FDE) では、異なるパスのドップラー シフトによる ICI の影響を打ち消すことはできません。このセクションでは、QPSK マッピングされたシンボルの $$M$$ 行 $$N$$ 列のグリッドを形成し、OFDM と OTFS の両方を使用して高移動度チャネル経由で送信し、パフォーマンスを比較します。

送信用のデータを生成します。

% Data generation
Xgrid = zeros(M,N);
Xdata = randi([0,1],2*M,N);
Xgrid(1:M,:) = pskmod(Xdata,4,pi/4,InputType="bit");

高ドップラー チャネル経由の OFDM

OFDM では、既知のシンボル (パイロット) を送信し、受信機でのパイロットの歪みを測定することでチャネルを推定します。$$N$$ 個のシンボルすべてにわたり、$$M$$ 個のサブキャリアすべてに対してパイロットを送信することにより、チャネルを推定します。

% Transmit pilots over all subcarriers and symbols to sound the channel
txOut = ofdmmod(exp(1i*pi/4)*ones(M,N),M,padLen);       % transmit pilots over the entire grid
dopplerOut = dopplerChannel(txOut,fsamp,chanParams);    % send through channel
chOut = awgn(dopplerOut,SNRdB,'measured');              % add noise
Yofdm = ofdmdemod(chOut(1:(M+padLen)*N),M,padLen);      % demodulate
Hofdm = Yofdm * conj(Pdd(1,pilotBin)) / (abs(Pdd(1,pilotBin))^2 + n0); % LMMSE channel estimate

OFDM を使用してデータ グリッドを送信します。測定されたチャネル推定値を使用して、すべてのシンボルに対してシングルタップ FDE を使用してイコライズします。

% Transmit data over the same channel and use channel estimates to equalize
txOut = ofdmmod(Xgrid,M,padLen);                        % transmit data grid

dopplerOut = dopplerChannel(txOut,fsamp,chanParams);    % send through channel
chOut = awgn(dopplerOut,SNRdB,'measured');              % add noise

rxWindow = chOut(1:(M+padLen)*N);
Yofdm = ofdmdemod(rxWindow,M,padLen);                   % demodulate

Xhat_ofdm = conj(Hofdm) .* Yofdm ./ (abs(Hofdm).^2+n0); % equalize with LMMSE

受信したコンスタレーションを表示します。SNR が高くても、コンスタレーションにはノイズが含まれています。2 つの散乱体のドップラー シフトをゼロに設定し、コンスタレーションのエラー ベクトル振幅 (EVM) が減少することを観察することで、ノイズが主に ICI によるものであることを検証できます。

constDiagOFDM = comm.ConstellationDiagram( ...
    ReferenceConstellation=pskmod(0:3,4,pi/4), ...
    AxesLimits=[-2 2], ...
    Title='OFDM with Single-Tap FDE');
constDiagOFDM(Xhat_ofdm(:));

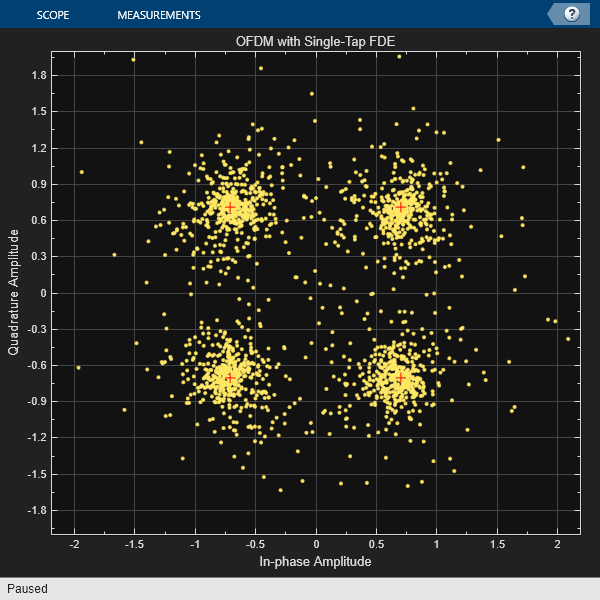
XhatDataOFDM = pskdemod(Xhat_ofdm,4,pi/4, ...
    OutputType="bit",OutputDataType="logical");         % decode
[~,berOFDM] = biterr(Xdata,XhatDataOFDM);
fprintf('OFDM BER with single-tap equalizer = %3.3e\n', berOFDM);

OFDM BER with single-tap equalizer = 1.693e-02

ノイズが少ない場合に BER がどれだけ高くなるかを観察します。サイクリック プレフィックスは ISI を軽減できますが、時間-周波数領域でのシングルタップ イコライゼーションではドップラーシフトされたパスによって発生する ICI を補正できず、その結果、中程度の BER が発生します。

高ドップラー チャネル経由の OTFS

OTFS 変調を使用して同じデータ グリッドを送信します。

% OTFS modulation
txOut = helperOTFSmod(Xgrid,padLen,padType);

% Add channel and noise
dopplerOut = dopplerChannel(txOut,fsamp,chanParams);
chOut = awgn(dopplerOut,SNRdB,'measured');

一般的な信号モデルは $$y=Gx+n$$ として与えられます。ここで、$$x$$ と $$y$$ は、それぞれ長さ $$MN$$ の、チャネルに送信される時間領域信号と、時間領域チャネル行列 $$G$$ から受信される信号です。$$G$$ が既知である場合、LMMSE を使用してチャネルをイコライズできます [4]。行列形式では、LMMSE は次のように表されます。

$$\underset{}{\overset{ˆ}{x}}=(G^{H}G+{\sigma }_n^2{I}_{MN}{)}^{-1}{G}^{H}y.$$

時間領域でイコライズすることにより、個々のパスの遅延とドップラー シフトの情報を使用して ICI を除去できます。先ほど求めた遅延-ドップラー チャネル パラメーターの推定値からチャネル行列を形成します。

% Form G matrix using channel estimates
G = getG(M,N,chanEst,padLen,padType);

遅延-ドップラー領域で LMMSE を使用して受信データをイコライズおよび検出します。ノイズ パワーは既知であると仮定します。

rxWindow = chOut(1:numSamps);
y_otfs = ((G'*G)+n0*eye(Meff*N)) \ (G'*rxWindow); % LMMSE

Xhat_otfs = helperOTFSdemod(y_otfs,M,padLen,0,padType); % OTFS demodulation

受信したコンスタレーションが OFDM コンスタレーションよりもクリーンであることを示します。

constDiagOTFS = comm.ConstellationDiagram( ...
    ReferenceConstellation=pskmod(0:3,4,pi/4), ...
    AxesLimits=[-2 2], ...
    Title='OTFS with Time-Domain LMMSE Equalization');
constDiagOTFS(Xhat_otfs(:));

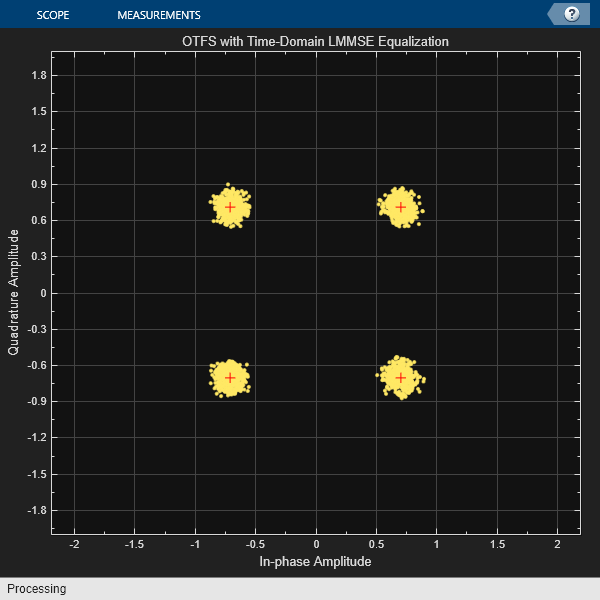
XhatDataOTFS = pskdemod(Xhat_otfs,4,pi/4,OutputType="bit",OutputDataType="logical");
[~,berOTFS] = biterr(Xdata,XhatDataOTFS);
fprintf('OTFS BER with LMMSE equalization = %3.3e\n', berOTFS);

OTFS BER with LMMSE equalization = 0.000e+00

OTFS は ICI を大幅に削減できます。

まとめ

OTFS は、モバイル環境における高ドップラーの影響を相殺する良好な変調スキームです。この例では、遅延-ドップラー領域の概念、その領域で送信されたシンボルに対する移動体チャネルの影響、および OTFS シンボルを変調および復調する方法について説明します。OTFS と OFDM を使用して同じチャネルで同じデータを送信し、簡単なチャネル推定とイコライゼーションの後で BER を観察すると、OTFS は ICI を効果的に抑制しますが、OFDM では抑制できないことがわかります。

より正確なチャネル推定とより効率的なデータ検出方法については、参考文献に記載されています。この例では、単純なチャネル推定手法と簡単なチャネル イコライゼーション手法を使用して、高ドップラー チャネルにおける OTFS の OFDM に対する有意性を示します。

参考文献

1.R. Hadani et al. "Orthogonal Time Frequency Space Modulation." 2017 IEEE Wireless Communications and Networking Conference (WCNC). San Francisco, CA, USA, 2017, pp. 1-6.

2. 3GPP TSG RA WG1. OTFS modulation waveform and reference signals for new RAT: Meeting #84-bis R1-162930. Busan, South Korea: 3GPP, 2016.

3.TSDSI. “6G Use Cases and Enabling Technologies.” Oct. 2022.

4.Y. Hong, T. Thaj, and E. Viterbo. Delay-Doppler Communications. London, Elsevier 2022.

サポート関数

function y = dopplerChannel(x,fs,chanParams)
    % Form an output vector y comprising paths of x with different
    % delays, Dopplers, and complex gains
    numPaths = length(chanParams.pathDelays);
    maxPathDelay = max(chanParams.pathDelays);
    txOutSize = length(x);
    
    y = zeros(txOutSize+maxPathDelay,1);
    
    for k = 1:numPaths
        pathOut = zeros(txOutSize+maxPathDelay,1);

        % Doppler
        pathShift = frequencyOffset(x,fs,chanParams.pathDopplerFreqs(k));
    
        % Delay and gain
        pathOut(1+chanParams.pathDelays(k):chanParams.pathDelays(k)+txOutSize) = ...
            pathShift * chanParams.pathGains(k);
            
        y = y + pathOut;
    end
end

function G = getG(M,N,chanParams,padLen,padType)
    % Form time domain channel matrix from detected DD paths
    if strcmp(padType,'ZP') || strcmp(padType,'CP')
        Meff = M + padLen;  % account for subsymbol pad length in forming channel
        lmax = padLen;      % max delay
    else
        Meff = M;
        lmax = max(chanParams.pathDelays);  % max delay
    end
    MN = Meff*N;
    P = length(chanParams.pathDelays);  % number of paths
    
    % Form an array of channel responses for each path
    g = zeros(lmax+1,MN);
    for p = 1:P
        gp = chanParams.pathGains(p);
        lp = chanParams.pathDelays(p);
        vp = chanParams.pathDopplers(p); 

        % For each DD path, compute the channel response.
        % Each path is a complex sinusoid at the Doppler frequency (kp)
        % shifted by a delay (lp) and scaled by the path gain (gp)
        g(lp+1,:) = g(lp+1,:) + gp*exp(1i*2*pi/MN * vp*((0:MN-1)-lp));
    end    

    % Form the MN-by-MN channel matrix G
    G = zeros(MN,MN);
    % Each DD path is a diagonal in G offset by its path delay l
    for l = unique(chanParams.pathDelays).'
        G = G + diag(g(l+1,l+1:end),-l);
    end
end

参考

トピック

• SC-FDMA vs. OFDM Modulation