このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
軌道伝播モデルの比較
この例では、二体ケプラー軌道伝播関数と簡易一般摂動法 4 (SGP4)軌道プロパゲーターによって予測される軌道を比較します。軌道プロパゲーターは、主に天体の重力場の影響を受ける宇宙空間におけるオブジェクトの位置と速度を計算するソルバーです。
二体ケプラー軌道プロパゲーターは、地球の重力場のみを考慮し、他の天体や環境要因の影響を無視する簡略化されたモデルに依存しています。このモデルでは、地球は均一な密度を持つ球体であると仮定しています。このアプローチにより、このプロパゲーターは、説明したモデルの中で最も精度が低くなります。
対照的に、 SGP4軌道プロパゲーターは、地球の形状と大気抵抗による永年的および周期的な軌道擾乱の両方を組み込んでおり、軌道周期が 225 分未満の地球近傍軌道上の衛星に適しています。衛星の軌道周期が 225 分を超える場合、 SGP4軌道プロパゲーターは太陽と月の重力も考慮します。
衛星シナリオを作成する
satelliteScenario 関数を使用して衛星シナリオを作成します。datetime 関数を使用して、開始時刻を 2020 年 5 月 11 日PM12 時 35 分 38 秒 (UTC) に設定し、終了時刻を 2020 年 5 月 13 日午後 12 時 35 分 38PM(UTC) に設定します。サンプル時間を 60 秒に設定します。
startTime = datetime(2020,5,11,12,35,38); stopTime = startTime + days(2); sampleTime = 60; sc = satelliteScenario(startTime,stopTime,sampleTime)
sc =
satelliteScenario with properties:
StartTime: 11-May-2020 12:35:38
StopTime: 13-May-2020 12:35:38
SampleTime: 60
AutoSimulate: 1
CentralBodyOptions: [1×1 Aero.satellitescenario.CentralBodyOptions]
Satellites: [1×0 matlabshared.satellitescenario.Satellite]
GroundStations: [1×0 matlabshared.satellitescenario.GroundStation]
Platforms: [1×0 matlabshared.satellitescenario.Platform]
Viewers: [0×0 matlabshared.satellitescenario.Viewer]
AutoShow: 1
衛星シナリオに衛星を追加する
satellite 関数を使用して、2 行要素 ( TLE ) ファイル eccentricOrbitSatellite.tle から衛星シナリオに 2 つの衛星を追加します。TLEは、特定の時間に定義された地球周回オブジェクトの軌道要素をエンコードするために使用されるデータ形式です。最初の衛星に二体ケプラー軌道プロパゲーターを割り当て、2番目の衛星にSGP4ます。
tleFile = "eccentricOrbitSatellite.tle"; satTwoBodyKeplerian = satellite(sc,tleFile, ... "Name","satTwoBodyKeplerian", ... "OrbitPropagator","two-body-keplerian")
satTwoBodyKeplerian =
Satellite with properties:
Name: satTwoBodyKeplerian
ID: 1
ConicalSensors: [1x0 matlabshared.satellitescenario.ConicalSensor]
Gimbals: [1x0 matlabshared.satellitescenario.Gimbal]
Transmitters: [1x0 satcom.satellitescenario.Transmitter]
Receivers: [1x0 satcom.satellitescenario.Receiver]
Accesses: [1x0 matlabshared.satellitescenario.Access]
Eclipse: [1x0 Aero.satellitescenario.Eclipse]
GroundTrack: [1x1 matlabshared.satellitescenario.GroundTrack]
Orbit: [1x1 matlabshared.satellitescenario.Orbit]
CoordinateAxes: [1x1 matlabshared.satellitescenario.CoordinateAxes]
OrbitPropagator: two-body-keplerian
MarkerColor: [0.059 1 1]
MarkerSize: 6
ShowLabel: true
LabelFontColor: [1 1 1]
LabelFontSize: 15
Visual3DModel:
Visual3DModelScale: 1
satSGP4 = satellite(sc,tleFile, ... "Name","satSGP4", ... "OrbitPropagator","sgp4")
satSGP4 =
Satellite with properties:
Name: satSGP4
ID: 2
ConicalSensors: [1x0 matlabshared.satellitescenario.ConicalSensor]
Gimbals: [1x0 matlabshared.satellitescenario.Gimbal]
Transmitters: [1x0 satcom.satellitescenario.Transmitter]
Receivers: [1x0 satcom.satellitescenario.Receiver]
Accesses: [1x0 matlabshared.satellitescenario.Access]
Eclipse: [1x0 Aero.satellitescenario.Eclipse]
GroundTrack: [1x1 matlabshared.satellitescenario.GroundTrack]
Orbit: [1x1 matlabshared.satellitescenario.Orbit]
CoordinateAxes: [1x1 matlabshared.satellitescenario.CoordinateAxes]
OrbitPropagator: sgp4
MarkerColor: [0.059 1 1]
MarkerSize: 6
ShowLabel: true
LabelFontColor: [1 1 1]
LabelFontSize: 15
Visual3DModel:
Visual3DModelScale: 1
衛星とその軌道を可視化する
衛星シナリオ ビューアーを起動し、satelliteScenarioViewer 関数を使用して衛星シナリオを可視化します。satSGP4 の可視化を緑色に設定します。
v = satelliteScenarioViewer(sc); satSGP4.MarkerColor = "green"; satSGP4.Orbit.LineColor = "green"; satSGP4.LabelFontColor = "green";

camtarget 機能を使用して、カメラを satTwoBodyKeplerian にフォーカスします。
camtarget(v,satTwoBodyKeplerian);
衛星シナリオ ビューアー ウィンドウ内の任意の場所を左クリックし、クリックしたままマウスを動かすと、カメラがパンします。スクロール ホイールを使用してズーム レベルを調整し、3 つの衛星すべてを表示します。
衛星の動きを動的アニメーションで可視化する
衛星シナリオで play 関数を使用して、衛星の動きを可視化します。play 関数は、SampleTime で指定されたステップ サイズを使用して、指定された StartTime から StopTime までの衛星シナリオをシミュレートし、結果を衛星シナリオ ビューアーで再生します。
play(sc)
再生速度と方向を制御するには、衛星シナリオ ビューアー ウィンドウの下部にある再生コントロールを使用します。camtarget 機能を使用してカメラを再び satTwoBodyKeplerian にフォーカスし、ズーム レベルを調整して 3 つの衛星すべてを視界に収めます。
camtarget(v,satTwoBodyKeplerian);
3 つの衛星の位置は時間の経過とともに変化します。

衛星の位置と速度の履歴を取得する
states 関数を使用して、地心天体基準座標系 (GCRF) 内の衛星の位置と速度の履歴を返します。
[positionTwoBodyKeplerian,velocityTwoBodyKeplerian,time] = states(satTwoBodyKeplerian); [positionSGP4,velocitySGP4] = states(satSGP4);
二体ケプラーの予測に対する相対位置の大きさをプロットする
vecnorm 関数を使用して、satTwoBodyKeplerian に対する satSGP4 の相対位置の大きさを計算します。
sgp4RelativePosition = vecnorm(positionSGP4 - positionTwoBodyKeplerian,2,1);
plot 関数を使用して、satTwoBodyKeplerian に対する satSGP4 の相対位置の大きさをキロメートル単位でプロットします。
sgp4RelativePositionKm = sgp4RelativePosition/1000; plot(time,sgp4RelativePositionKm) xlabel("Time") ylabel("Relative position (km)") grid on
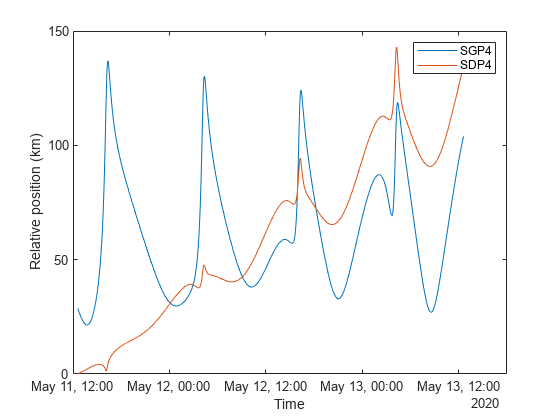
時間の経過とともに、satSGP4 の位置は satTwoBodyKeplerian の位置からずれていきます。これは、satSGP4 が地球の形状と大気抵抗によって引き起こされる永年的および周期的な軌道摂動を考慮しているためです。TLEファイルから計算された軌道周期は 225 分より大きいため、satSGP4 の位置は太陽と月の重力も考慮に入れています。orbitalElements 関数を使用して軌道周期を取得できます。
elSatSGP4 = orbitalElements(satSGP4);
elSatSGP4.Period/60 % minutesans = 720
satTwoBodyKeplerian の位置は、地球の周りの球状の重力ポテンシャルを想定しており、すべての摂動効果は無視されます。
二体ケプラーの予測に対する相対速度の大きさのプロット
vecnorm 関数を使用して、satTwoBodyKeplerian に対する satSGP4 の相対速度の大きさを計算します。
sgp4RelativeVelocity = vecnorm(velocitySGP4 - velocityTwoBodyKeplerian,2,1);
plot 関数を使用して、satTwoBodyKeplerian に対する satSGP4 の相対速度の大きさ (メートル/秒) をプロットします。
plot(time,sgp4RelativeVelocity) xlabel("Time") ylabel("Velocity deviation (m/s)") grid on
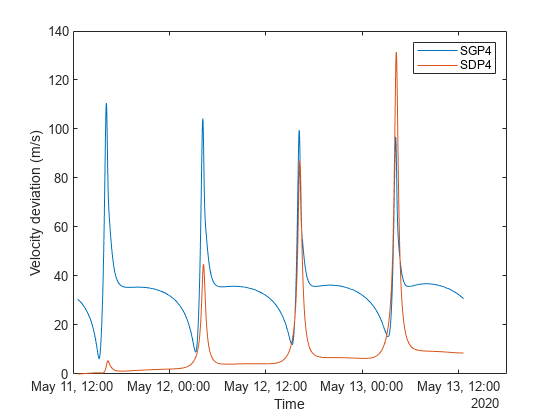
時間の経過とともに、位置に影響を与える同じ要因により、satSDP4 の速度は satTwoBodyKeplerian の速度から逸脱します。グラフのスパイクは近点(軌道上で地球の質量中心に最も近い点)に対応しており、ここでは速度の誤差がより顕著になります。
グラフに見られる変化は、 2 つの軌道プロパゲーターが提供する精度のレベルが異なることを強調しています。二体ケプラー軌道プロパゲーターは、地球の重力場を球形として単純化し、軌道摂動の他のすべての発生源を無視するため、精度が低くなります。SGP4軌道プロパゲーターは、地球の扁平率と大気抵抗の影響を考慮して精度を高めます。この例の衛星の軌道周期は 225 分を超えるため、 SGP4軌道プロパゲーターは太陽と月の重力も考慮します。