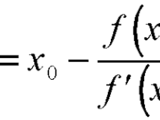The Newton - Raphson Method
"The Newton - Raphson Method" uses one initial approximation to solve a given equation y = f(x).In this method the function f(x) , is approximated by a tangent line, whose equation is found from the value of f(x) and its first derivative at the initial approximation.
The tangent line then intersects the X - Axis at second point. This second point is again used as next approximation to find the third point.
The script proceeds in the same way and performs upto 100 iterations. The Accuracy required
(required no. of decimal places) is taken as input from the user. The error between solutions of each iteration is checked every time and if found less than required accuracy, the iterations are stopped.
引用
अंबरीश प्रशांत चांदूरकर Ambarish Prashant Chandurkar (2026). The Newton - Raphson Method (https://jp.mathworks.com/matlabcentral/fileexchange/68885-the-newton-raphson-method), MATLAB Central File Exchange. 取得日: .
MATLAB リリースの互換性
プラットフォームの互換性
Windows macOS Linuxカテゴリ
- Mathematics and Optimization > Optimization Toolbox > Systems of Nonlinear Equations > Newton-Raphson Method >
タグ
謝辞
ヒントを与えたファイル: Newton-Raphson-Secant Method