Harmonic excitation of a SDOF
Harmonic excitation of a SDOF
Summary
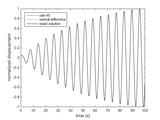
The exact solution of a damped Single Degree Of Freedom (SDOF) system is excited by a harmonic force is calculated [1]. It is compared to the numerical solution provided by the Matlab built-in function ode 45, the central difference method, Newmark method and the 4th order Runge-Kutta method, the implementation of which is based on the book from S. Rao [2].
Content
The repositroy contains:
- The function RK4.m, which solves numerically the equations of motion of a damped system with the 4th order Runge-Kutta method
- The function Newmark.m, which solves numerically the equations of motion of a damped system with Newmark's method
- The function CentDiff.m, which solves numerically the equations of motion of a damped system with the central difference method
- A Matlab livescript Documentation.mlx for the documentation
References
[1] Daniel J. Inman, Engineering Vibrations, Pearson Education, 2013
[2] Singiresu S. Rao, Mechanical Vibrations,Prentice Hall, 2011
引用
E. Cheynet (2024). Harmonic excitation of a SDOF (https://github.com/ECheynet/Excitation_SDOF/releases/tag/v2.3), GitHub. に取得済み.
MATLAB リリースの互換性
プラットフォームの互換性
Windows macOS Linuxカテゴリ
- MATLAB > Mathematics > Numerical Integration and Differential Equations >
- Engineering > Mechanical Engineering > Acoustics, Noise and Vibration >
タグ
謝辞
ヒントを与えたファイル: Damping ratio estimation from ambient vibrations (SDOF)
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!| バージョン | 公開済み | リリース ノート | |
|---|---|---|---|
| 2.3 | See release notes for this release on GitHub: https://github.com/ECheynet/Excitation_SDOF/releases/tag/v2.3 |
||
| 2.2.2 | See release notes for this release on GitHub: https://github.com/ECheynet/Excitation_SDOF/releases/tag/v2.2.2 |
||
| 2.2.1 | See release notes for this release on GitHub: https://github.com/ECheynet/Excitation_SDOF/releases/tag/v2.2.1 |
||
| 2.2 | Added project website |
||
| 2.1.0.0 | The inputs of the Newmark-Beta funciton are ordered to be consistent with the function CentDiff |
||
| 2.0.0.0 | Added Newmark and Runge-Kutta methods |
||
| 1.0.0.0 | - picture added |