eqn =
メインコンテンツ
結果:
I'm beginning this MATLAB-based numerical methods class, and as I was thinking back to my previous MATLAB/Simulink classes, I definitely remember some projects more fondly than others. One of my most memorable was where I had to use MATLAB to analyze electrocardiogram (ECG) peaks. What about you guys? What are some of the best (or worst 🤭) MATLAB projects or assignments you've been given in the past?
Speaking as someone with 31+ years of experience developing and using imshow, I want to advocate for retiring and replacing it.
The function imshow has behaviors and defaults that were appropriate for the MATLAB and computer monitors of the 1990s, but which are not the best choice for most image display situations in today's MATLAB. Also, the 31 years have not been kind to the imshow code base. It is a glitchy, hard-to-maintain monster.
My new File Exchange function, imview, illustrates the kind of changes that I think should be made. The function imview is a much better MATLAB graphics citizen and produces higher quality image display by default, and it dispenses with the whole fraught business of trying to resize the containing figure. Although this is an initial release that does not yet support all the useful options that imshow does, it does enough that I am prepared to stop using imshow in my own work.
The Image Processing Toolbox team has just introduced in R2024b a new image viewer called imageshow, but that image viewer is created in a special-purpose window. It does not satisfy the need for an image display function that works well with the axes and figure objects of the traditional MATLAB graphics system.
I have published a blog post today that describes all this in more detail. I'd be interested to hear what other people think.
Note: Yes, I know there is an Image Processing Toolbox function called imview. That one is a stub for an old toolbox capability that was removed something like 15+ years ago. The only thing the toolbox imview function does now is call error. I have just submitted a support request to MathWorks to remove this old stub.
The int function in the Symbolic Toolbox has a hold/release functionality wherein the expression can be held to delay evaluation
syms x I
eqn = I == int(x,x,'Hold',true)
which allows one to show the integral, and then use release to show the result
release(eqn)
Maybe it would be nice to be able to hold/release any symbolic expression to delay the engine from doing evaluations/simplifications that it typically does. For example:
x*(x+1)/x, sin(sym(pi)/3)
If I'm trying to show a sequence of steps to develop a result, maybe I want to explicitly keep the x/x in the first case and then say "now the x in the numerator and denominator cancel and the result is ..." followed by the release command to get the final result.
Perhaps held expressions could even be nested to show a sequence of results upon subsequent releases.
Held expressions might be subject to other limitations, like maybe they can't be fplotted.
Seems like such a capability might not be useful for problem solving, but might be useful for exposition, instruction, etc.
Watt's Up with Electric Vehicles?EV modeling Ecosystem (Eco-friendly Vehicles), V2V Communication and V2I communications thereby emitting zero Emissions to considerably reduce NOx ,Particulates matters,CO2 given that Combustion is always incomplete and will always be.
Reduction of gas emissions outside to the environment will improve human life span ,few epidemic diseases and will result in long life standard
We will be updating the MATLAB Answers infrastructure at 1PM EST today. We do not expect any disruption of service during this time. However, if you notice any issues, please be patient and try again later. Thank you for your understanding.
Always and almost immediately!
26%
Never
30%
After validating existing code
15%
Y'all get the new releases?
29%
1843 票
Many of my best friends at MathWorks speak Spanish as their first language and we have a large community of Spanish-speaking users. You can see good evidence of this by checking out our relatively new Spanish YouTube channel which recently crossed the 10,000 subscriber mark
I've always used MATLAB with other languages. In the early days, C and C++ via mex files were the most common ways I spliced two languages together. Other than that I've also used MATLAB with Java, Excel and even Fortran.
In more recent years, Python is the language I tend to use most alongside MATLAB and support for this combination is steadily improving. In my latest blog post, I show how easy it has become to use Python's Numpy with MATLAB.
Have you used this functionality much? If so, what for? How well did it work for you?
I am inspired by the latest video from YouTube science content creator Veritasium on his distinct yet thorough explanation on how rainbows work. In his video, he set up a glass sphere experiment representing how light rays would travel inside a raindrop that ultimately forms the rainbow. I highly recommend checking it out.
In the meantime, I created an interactive MATLAB App in MATLAB Online using App Designer to visualize the light paths going through a spherical raindrop with numerical calculations along the way. While I've seen many diagrams out there showing the light paths, I haven't found any doing calculations in each step. Hence I created an app in MATLAB to show the calculations along with the visualizations as one varies the position of the incoming light ray.
Demo video:
For more information about the app and how to open it and play around with it in MATLAB Online, please check out my blog article:
Our MathWorks Usability Team is working on an accessibility project and they want to interview people who use MATLAB and also have experience with screen readers.
If you fit the criteria and are interested, sign up here https://www.mathworks.com/products/usability.html?tfa_30=A11Y
I wish I knew more about the intended evolution of the capabilities of the function arguments block. I love implementing function syntaxes using this relatively new form, but it doesn't yet handle some function syntax design patterns that I think are valuable and worth keeping.
For example, some functions take an input quantity that can something numeric, or it can be an option string that descriptively names a particular value of that quantity. One example is dateshift(t,"dayofweek",dow), where dow can be an integer from 1 to 7, or it can be one of the option strings "weekday" or "weekend".
Another example is Image Processing Toolbox that take a connectivity specifier as input. The function bwconncomp is one particular case. Connectivity can be specified using certain scalars, certain arrays, or the option string "maximal".
I think this is a worthwhile function design pattern, but I don't think the arguments block validation functionality supports it well (unless you use a lot of extra code that duplicates standard MATLAB behavior, which undermines the value of the arguments block).
MathWorkers - believe me, I know that it is not in your DNA to discuss future features. But would anyone care to offer a hint about directions for the arguments block functionality?
I am very excited to share my new book "Data-driven method for dynamic systems" available through SIAM publishing: https://epubs.siam.org/doi/10.1137/1.9781611978162
This book brings together modern computational tools to provide an accurate understanding of dynamic data. The techniques build on pencil-and-paper mathematical techniques that go back decades and sometimes even centuries. The result is an introduction to state-of-the-art methods that complement, rather than replace, traditional analysis of time-dependent systems. One can find methods in this book that are not found in other books, as well as methods developed exclusively for the book itself. I also provide an example-driven exploration that is (hopefully) appealing to graduate students and researchers who are new to the subject.
Each and every example for the book can be reproduced using the code at this repo: https://github.com/jbramburger/DataDrivenDynSyst
Hope you like it!
At the present time, the following problems are known in MATLAB Answers itself:
- Symbolic output is not displaying. The work-around is to disp(char(EXPRESSION)) or pretty(EXPRESSION)
- Symbolic preferences are sometimes set to non-defaults
Hello, MATLAB fans!
For years, many of you have expressed interest in getting your hands on some cool MathWorks merchandise. I'm thrilled to announce that the wait is over—the MathWorks Merch Shop is officially open!

In our shop, you'll find a variety of exciting items, including baseball caps, mugs, T-shirts, and YETI bottles.
Visit the shop today and explore all the fantastic merchandise we have to offer. Happy shopping!
Just shared an amazing YouTube video that demonstrates a real-time PID position control system using MATLAB and Arduino.
I don't like the change
16%
I really don't like the change
29%
I'm okay with the change
24%
I love the change
11%
I'm indifferent
11%
I want both the web & help browser
11%
38 票

You can make a lot of interesting objects with matlab primitive shapes (e.g. "cylinder," "sphere," "ellipsoid") by beginning with some of the built-in Matlab primitives and simply applying deformations. The gif above demonstrates how the Manta animation was created using a cylinder as the primitive and successively applying deformations: (https://www.mathworks.com/matlabcentral/communitycontests/contests/8/entries/16252);
Similarly, last year a sphere was deformed to create a face in two of my submissions, for example, the profile in "waking":

You can piece-wise assemble images, but one of the advantages of creating objects with deformations is that you have a parametric representation of the surface. Creating a higher or lower polygon rendering of the surface is as simple as declaring the number of faces in the orignal primitive. For example here is the scene in "snowfall" using sphere with different numbers of input faces:
sphere(100)

sphere(500)

High poly models aren't always better. Low-polygon shapes can sometimes add a little distance from that low point in the uncanny valley.
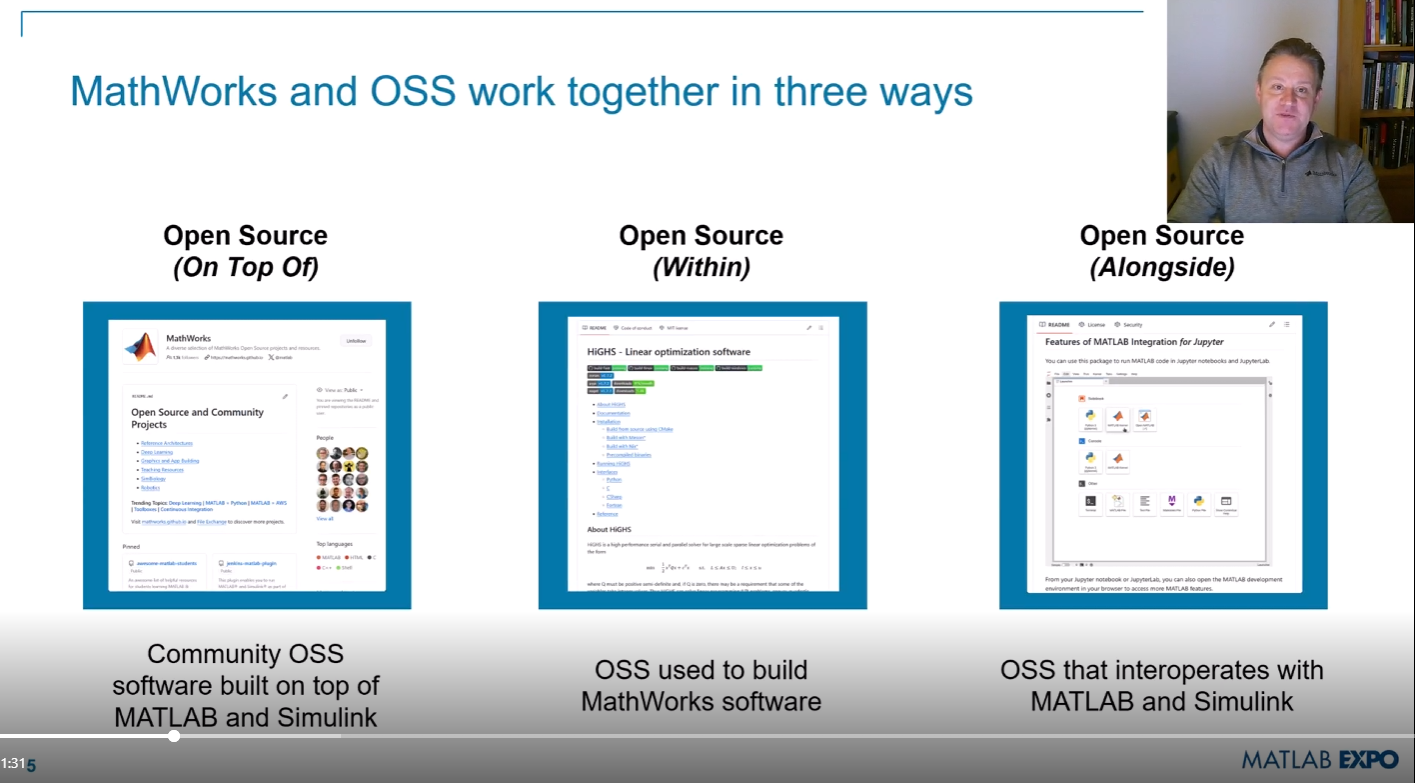
Next week is MATLAB EXPO week and it will be the first one that I'm presenting at! I'll be giving two presentations, both of which are related to the intersection of MATLAB and open source software.
- Open Source Software and MATLAB: Principles, Practices, and Python Along with MathWorks' Heather Gorr. We we discuss three different types of open source software with repsect to their relationship to MATLAB
- The CLASSIX Story: Developing the Same Algorithm in MATLAB and Python Simultaneously A collaboration with Prof. Stefan Guettel from University of Manchester. Developing his clustering algorithm, CLASSIX, in both Python and MATLAB simulatenously helped provide insights that made the final code better than if just one language was used.
There are a ton of other great talks too. Come join us! (It's free!) MATLAB EXPO 2024
Hi MATLAB Central community! 👋
I’m currently working on a project where I’m integrating MATLAB analytics into a mobile app, mainly to handle data-heavy tasks like processing sensor data and running predictive models. The app is built for Android, and while it’s not entirely MATLAB-based, I use MATLAB for a lot of data preprocessing and model training.
I wanted to reach out and see if anyone else here has experience with using MATLAB for similar mobile or embedded applications. Here are a few areas I’m focusing on:1. Optimizing MATLAB Code for Mobile Compatibility
I’ve found that some MATLAB functions work perfectly on desktop but may run slower or encounter limitations on mobile. I’ve tried using code generation and reducing function calls where possible, but I’m curious if anyone has other tips for optimizing MATLAB code for mobile environments?
2. Using MATLAB for Sensor Data Processing
I’m working with accelerometer and GPS data, and MATLAB has been great for preprocessing. However, I wonder if anyone has suggestions for handling large sensor datasets efficiently in MATLAB, especially if you've managed data in mobile contexts?
3. Integrating MATLAB Models into Mobile Apps
I’ve heard about using MATLAB Compiler SDK to integrate MATLAB algorithms into other environments. For those who have done this, what’s the best way to maintain performance without excessive computational strain on the device?
4. Data Visualization Tips
Has anyone had experience with mobile-friendly data visualizations using MATLAB? I’ve been using basic plots, but I’d love to know if there are any resources or toolboxes that make it easier to create lightweight, interactive visuals for mobile.
If anyone here has tips, tools, or experiences with MATLAB in mobile development, I’d love to hear them! Thanks in advance for any advice you can share!

