Use timeFrequencyScattering with default settings to create a joint time-frequency scattering (JTFS) network.
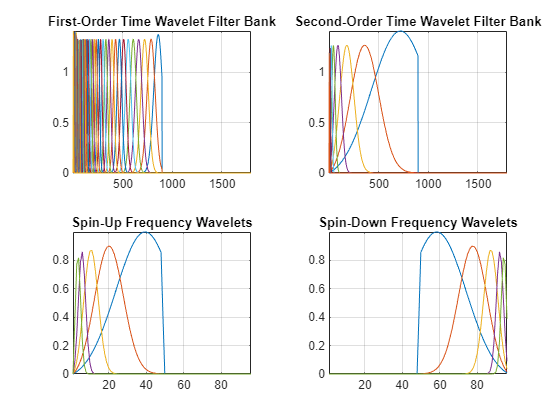
Plot the wavelet filters in the first- and second-order time filter banks, and the spin-up and spin-down wavelet filters. The filter magnitudes are not equal because, by default, the network attempts to approximate the Littlewood-Paley condition for the filters. You can change this default behavior through the EnergyCorrectFilters network property.
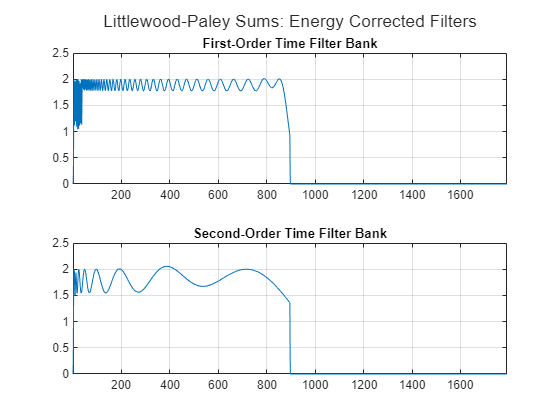
To see the effect of the approximation, use littlewoodPaleySum to plot the Littlewood-Paley sums of the first- and second-order time filter banks. In the theoretical best-case scenario, the Littlewood-Paley sum for these filters is a straight line equal to 2 from 0 to the Nyquist, and zero after that. Given the freedom you have in constructing the network, the best-case scenario is not possible. Therefore, the network approximates the filters so that the Littlewood-Paley sums are as close to 2 as possible.
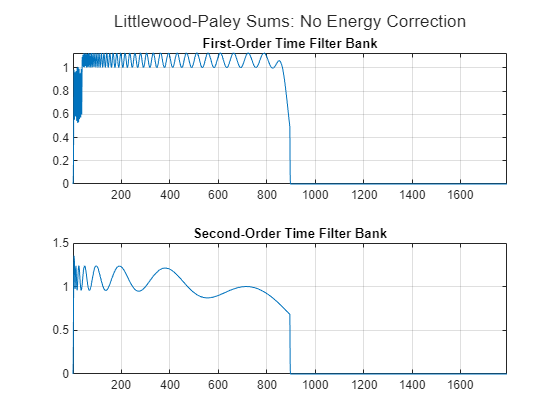
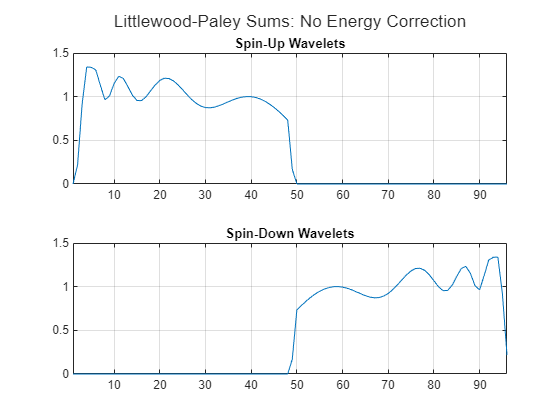
To see the impact of the energy correction, create a JTFS network with EnergyCorrectFilters set to false. Plot the Littlewood-Paley sums of the wavelet time filter banks. These sums are very different from the sums of the energy-corrected filters and far below the expected theoretical value of 2.
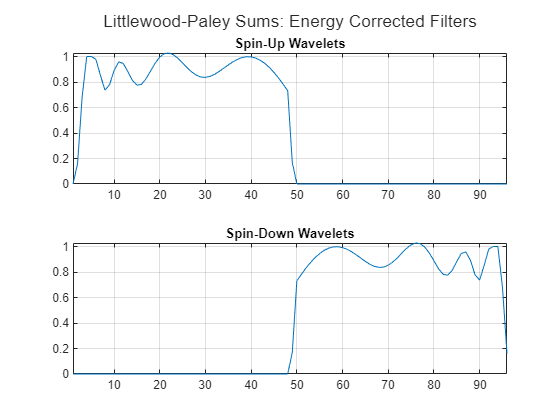
Repeat the same steps for the spin-up and spin-down wavelet filters. In the theoretical best-case scenario, the Littlewood-Paley sum for these filters would be a straight line equal to 1 across the entire range. As is the case for the time wavelet filters, it is not possible to achieve this theoretical value exactly.
Plot the Littlewood-Paley sums of the spin-up and spin-down wavelets in the default JTFS network.
Compare with a plot of the Littlewood-Paley sums using a JTFS network with EnergyCorrectFilters set to false. Without energy correction, the sums oscillate significantly above and below the expected theoretical value of 1. The sums of the spin-up and spin-down wavelets also exhibit downward and upward trends, respectively. This behavior does not occur for the energy-corrected filters.