biorfilt
Biorthogonal wavelet filter set
Syntax
Description
[
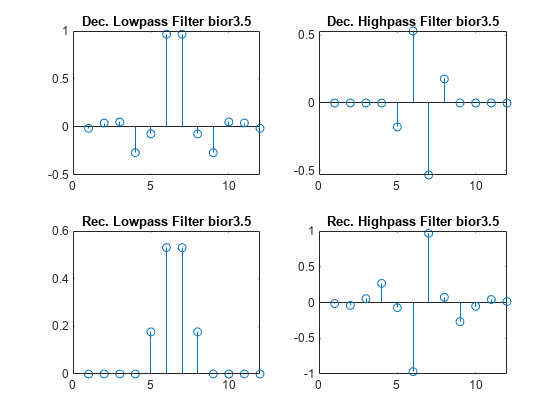
returns four filters associated with the
biorthogonal wavelet specified by decomposition
filter LoD,HiD,LoR,HiR] = biorfilt(DF,RF)DF and reconstruction
filter RF. These filters are
LoD— Decomposition lowpass filterHiD— Decomposition highpass filterLoR— Reconstruction lowpass filterHiR— Reconstruction highpass filter
[
returns eight filters, the first four associated
with the decomposition wavelet, and the last four
associated with the reconstruction wavelet.LoD1,HiD1,LoR1,HiR1,LoD2,HiD2,LoR2,HiR2] = biorfilt(DF,RF,'8')
Examples
Input Arguments
Output Arguments
More About
References
[1] Cohen, Albert. "Ondelettes, analyses multirésolution et traitement numérique du signal," Ph. D. Thesis, University of Paris IX, DAUPHINE. 1992.
[2] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.
Extended Capabilities
Version History
Introduced before R2006a