連続ウェーブレット変換および逆連続ウェーブレット変換

この例では、連続ウェーブレット変換 (CWT) と逆 CWT を使用する方法について説明します。

正弦波とインパルスの CWT

2 つのインパルスで区切られた、周波数がそれぞれ 100 Hz および 50 Hz の互いに素の 2 つの正弦波で構成される信号を作成し、プロットします。サンプリング周波数は 1 kHz で、総信号持続時間は 1 秒間です。100 Hz の正弦波は、データの最初の 250 ミリ秒間発生します。50 Hz の正弦波は、データの最後の 500 ミリ秒間発生します。インパルスは 650 ミリ秒と 750 ミリ秒で発生します。$$N(0,0.1{}^2)$$ の加法性ホワイト ガウス ノイズも信号に含まれます。650 ミリ秒のインパルスは可視ですが、750 ミリ秒のインパルスは時間領域データでは明らかに表示されません。

Fs = 1000;
t = 0:1/Fs:1-1/Fs;
x = zeros(size(t));
x([625,750]) = 2.5;
x = x+ cos(2*pi*100*t).*(t<0.25)+cos(2*pi*50*t).*(t>=0.5)+...
    0.1*randn(size(t));
plot(t.*1000,x)
grid on;
xlabel('msec'); ylabel('Amplitude');

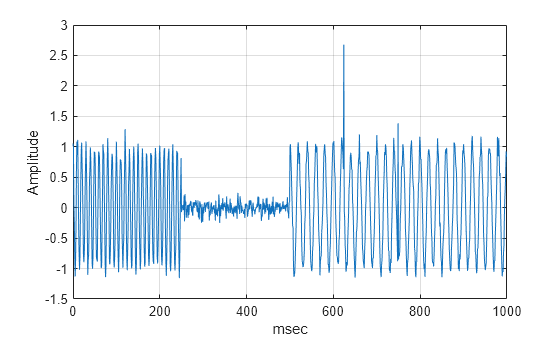
既定の解析 Morse ウェーブレットを使用して、CWT を求め、プロットします。

[cfs,f] = cwt(x,1000);
contour(t.*1000,f,abs(cfs));
xlabel('msec'); ylabel('Hz');
grid on;

CWT の絶対値は、互いに素の正弦波のサポートと、650 ミリ秒および 750 ミリ秒のインパルスの位置を正しく示しています。CWT の絶対値では、750 ミリ秒のインパルスがはっきりと見えています。これは、最も細かいスケールのウェーブレット係数のみをプロットすれば、特に顕著です。

plot(t.*1000,abs(cfs(1,:)))
grid on
title('Fine-Scale Wavelet Coefficient Moduli')
xlabel('msec')

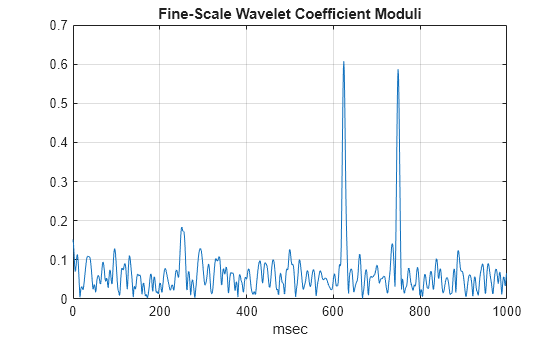
周波数局在型の逆 CWT

逆 CWT を使用すると、時系列内のイベントについて、周波数局在型の Approximation を作成できます。逆 CWT を使用して、前の例の 100 Hz 正弦波に対する Approximation を求めます。

xrec = icwt(cfs,[],f,[90 110]);
plot(t,x);
hold on;
plot(t,xrec,'r');
legend('Original Signal','Inverse CWT Approximation',...
    'Location','NorthEast');
grid on;

プロットをズームすると、100 Hz 成分がよく近似されていますが、50 Hz 成分は削除されていることがわかります。