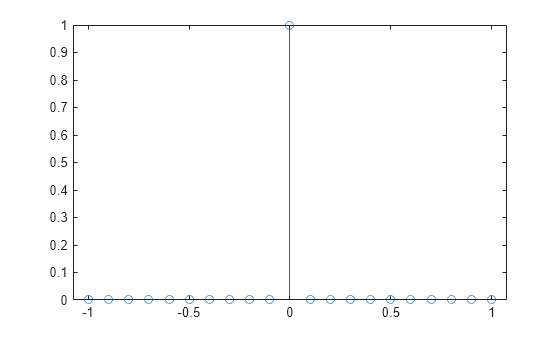dirac

ディラックのデルタ関数

構文

d = dirac(x)

d = dirac(n,x)

説明

d = dirac(x) は、x のディラック デルタ関数を表します。

d = dirac(n,x) は、x におけるディラック デルタ関数の n 次導関数を表します。

例

ディラックおよびへヴィサイドの関数を含む式の操作

ディラック デルタおよびへヴィサイドの関数を含む式の微分と積分を計算します。

へヴィサイド関数の 1 次および 2 次導関数を求めます。結果はディラック デルタ関数とその 1 次導関数となります。

syms x
diff(heaviside(x), x)
diff(heaviside(x), x, x)

ans =
dirac(x)
 
ans =
dirac(1, x)

ディラック デルタ関数の不定積分を求めます。int で返された結果には積分定数が含まれません。

int(dirac(x), x)

ans =
sign(x)/2

ディラックのデルタ関数を含む正弦関数の積分を求めます。

syms a
int(dirac(x - a)*sin(x), x, -Inf, Inf)

ans =
sin(a)

変数についての仮定の使用

dirac は変数についての仮定を考慮に入れます。

syms x real
assumeAlso(x ~= 0)
dirac(x)

ans =
0

計算を続けるため、x に設定された仮定を syms を使用して再作成することで消去します。

syms x

シンボリック行列のディラック デルタ関数求解

x のディラック デルタ関数とその最初の 3 つの導関数を計算します。

ベクトル n = [0,1,2,3] を使用して導関数の階数を指定します。関数 dirac はスカラーを n と同じサイズのベクトルに展開し、結果を計算します。

syms x
n = [0,1,2,3];
d = dirac(n,x)

d =
[ dirac(x), dirac(1, x), dirac(2, x), dirac(3, x)]

x に 0 を代入します。

subs(d,x,0)

ans =
[ Inf, -Inf, Inf, -Inf]

ディラックのデルタ関数のプロット

fplot を使用して、既定の区間 [-5 5] でディラックのデルタ関数をプロットできます。ただし、dirac(x) は x が 0 と等しい場合に Inf を返し、fplot は無限大をプロットしません。

シンボリック変数 x を宣言し、fplot を使用してシンボリック式 dirac(x) をプロットします。

syms x
fplot(dirac(x))

x が 0 と等しい場合に無限大を処理するには、シンボリック値ではなく数値を使用します。Inf の値を 1 に設定し、stem を使用してディラックのデルタ関数をプロットします。

x = -1:0.1:1;
y = dirac(x);
idx = y == Inf; % find Inf
y(idx) = 1;     % set Inf to finite value
stem(x,y)

入力引数

x — 入力

数値 | シンボリック数 | シンボリック変数 | シンボリック式 | シンボリック関数 | ベクトル | 行列 | 多次元配列

入力。実数を表す数値、シンボリック数、変数、式または関数として指定します。この入力はベクトル、行列、あるいは数値、シンボリック数、変数、式または関数の多次元配列でも可能です。

n — 微分の次数

非負の数値 | シンボリック変数 | シンボリック式 | シンボリック関数 | ベクトル | 行列 | 多次元配列

微分の次数。非負の数値、あるいは非負の数値を表すシンボリックな変数、式または関数として指定します。この入力はベクトル、行列、あるいは非負の数値、シンボリック数、変数、式または関数の多次元配列でも可能です。

詳細

ディラックのデルタ関数

ディラックのデルタ関数 δ(x) は、すべての x ≠ 0 に対し 0 の値を、x = 0 に対し ∞ をもちます。ディラックのデルタ関数は次の恒等性を満たします。

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta (x)dx}=1\text{.}$$

これはディラックのデルタ関数のヒューリスティックな定義です。ディラックデルタ関数を厳密に定義するには分布理論または測定理論が必要です。

任意の平滑化関数 f および実数 a について、ディラックのデルタ関数は次のプロパティをもちます。

$${\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta (x-a)f(x)}=f(a)\text{.}$$

ヒント

• 非ゼロの虚数部をもつ複素数値 x に対して dirac は NaN を返します。

• dirac は、シンボリック オブジェクトではない数値引数に対し浮動小数点の結果を返します。

• dirac は非スカラーの入力の要素ごとに働きます。

• 入力引数 x および n は同じサイズのベクトルまたは行列でなければなりません。またはいずれかがスカラーでなければなりません。一方の入力引数がスカラーであり、もう一方の入力引数がベクトルまたは行列である場合、dirac によってスカラーは、すべての要素がそのスカラーと等しい、もう一方の引数と同じサイズのベクトルまたは行列に拡張されます。

バージョン履歴

R2006a より前に導入

参考

heaviside | kroneckerDelta