シンボリック式のプロットの作成

シンボリックプロット関数を使用したプロット

MATLAB® では数値データをプロットするためのさまざまな手法を提供します。MATLAB のグラフ機能には、プロットツール、標準プロット関数、グラフ操作とデータ調査用ツール、ならびにグラフィックスを標準形式で印刷しエクスポートするためのツールがあります。Symbolic Math Toolbox™ ではこれらのグラフィカルな機能を拡張しており、次の関数を使用することによりシンボリック関数をプロットできます。

fplot - シンボリック式、方程式または関数の直交座標 2 次元プロットを作成。
fplot3 - 3 次元のパラメトリックプロットを作成。
fpolarplot - 極座標プロットを作成。("R2024a 以降")
fsurf - 表面プロットを作成。
fcontour - 等高線図を作成。
fmesh - メッシュプロットを作成。

fplot を使用してシンボリック式 $\sin (6 x)$ をプロットします。既定の設定では、fplot は範囲 $- 5 < x < 5$ を使用します。

syms x
fplot(sin(6*x))

fpolarplot を使用して、 $r$ (半径) および $θ$ (極角度) の極座標におけるシンボリック式または関数をプロットします。既定の設定では、fpolarplot はシンボリック式または関数を区間 $0 < θ < 2 π$ でプロットします。

シンボリック式 $\sin (6 t)$ を極座標にプロットします。

syms t
fpolarplot(sin(6*t))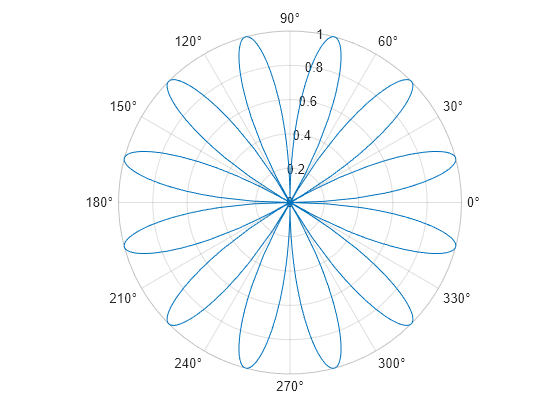

関数の数値的なプロット

式をシンボリックにプロットする代替方法として、subs を使用してシンボリック変数を数値に置き換えることができます。その後は、これらの数値を MATLAB のプロット関数で使用できます。

次のシンボリック式 u と v では、シンボリック変数 x と y を、meshgrid によって定義された数値に置き換えます。

syms x y
u = sin(x^2 + y^2);
v = cos(x*y);
[X,Y] = meshgrid(-1:.1:1,-1:.1:1);
U = subs(u,[x y],{X,Y});
V = subs(v,[x y],{X,Y});

これで、U と V を、標準の MATLAB プロット関数を使用してプロットできます。

関数 U(X,Y) と V(X,Y) によって定義されたベクトル場を、MATLAB 関数 quiver を使用してプロットします。

quiver(X,Y,U,V)

複数のシンボリック関数の 1 つのグラフ内でのプロット

シンボリック関数を順番に追加して、複数の関数を 1 つのグラフにプロットします。最初の関数をプロットした後、hold on コマンドを使用して、一連の関数を追加します。hold on コマンドは既存のプロットを保持します。hold on コマンドを使用しないと、新しいプロットごとに既存のプロットが置き換えられます。hold on コマンドを使用すると、新しいプロットがそれぞれ既存のプロットの上に表示されます。既定のプロット置き換え動作に戻すには、hold off コマンドを使用します。

fplot を使用して $f = e^{x} \sin (20 x)$ をプロットします。 $e^{x}$ と $- e^{x}$ のプロットを重ね合わせて、 $f$ の境界を赤い破線で示します。fplot によって返されたオブジェクトの DisplayName プロパティを使用してタイトルを設定します。

syms x y
f = exp(x)*sin(20*x)

f =  $\sin (20 x) e^{x}$

obj = fplot(f,[0 3]);
hold on
fplot(exp(x),[0 3],"--r")
fplot(-exp(x),[0 3],"--r")
title(obj.DisplayName)
hold off

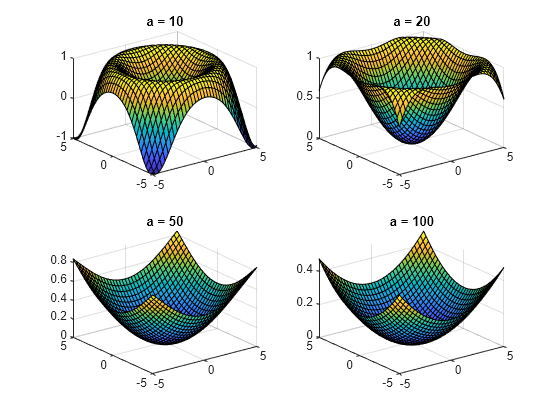
複数のシンボリック関数の 1 つの Figure 内でのプロット

subplot を使用して Figure ウィンドウを複数のサブプロットに分割することにより、1 つの Figure に複数の関数を並べて表示します。コマンド subplot(m,n,p) は、Figure ウィンドウを m 行 n 列のサブプロットの行列に分割し、サブプロット p を選択します。サブプロットを選択してプロットコマンドを使用し、複数のプロットを個別のサブプロットに表示します。複数のサブプロットでのプロットは、プロットを並べて比較する際に役立ちます。

subplot でサブプロットを並べて作成し、 $a = 10, 20, 50, 100$ に対する $\sin ((x^{2} + y^{2}) / a)$ のプロットを比較します。

syms x y a
f = sin((x^2 + y^2)/a);

subplot(2,2,1)
fsurf(subs(f,a,10))
title("a = 10")

subplot(2,2,2)
fsurf(subs(f,a,20))
title("a = 20")

subplot(2,2,3)
fsurf(subs(f,a,50))
title("a = 50")

subplot(2,2,4)
fsurf(subs(f,a,100))
title("a = 100")

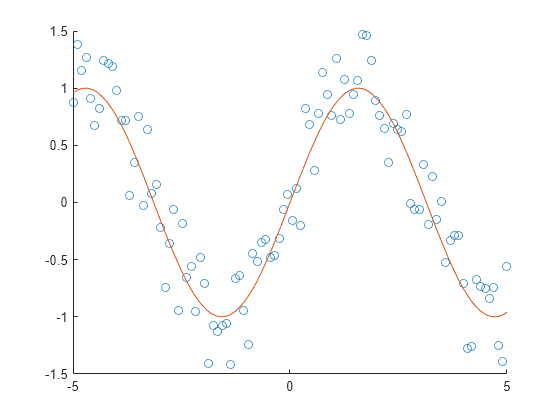
シンボリック関数のプロットと数値データのプロットの結合

MATLAB と Symbolic Math Toolbox の関数を組み合わせて使用し、数値データとシンボリックデータを同じグラフにプロットします。

$[- 5, 5]$ の範囲にある $x$ の数値に対して、 $y = \sin (x)$ を求めて乱数値を $y$ に加えると、ノイズを含む正弦曲線が返されます。scatter を使用して点 $(x 1, y 1), (x 2, y 2)$ などをプロットし、ノイズを含む正弦曲線を表示します。

figure
rng("default")
x = linspace(-5,5);
y = sin(x) + (-1).^randi(10,1,100).*rand(1,100)./2;
scatter(x,y)

正弦関数のプロットを重ね合わせて、点の基本構造を示します。最初に、hold on を使用して、散布図を保持します。続いて、fplot を使用して正弦関数をプロットします。

hold on
syms t
fplot(sin(t))
hold off

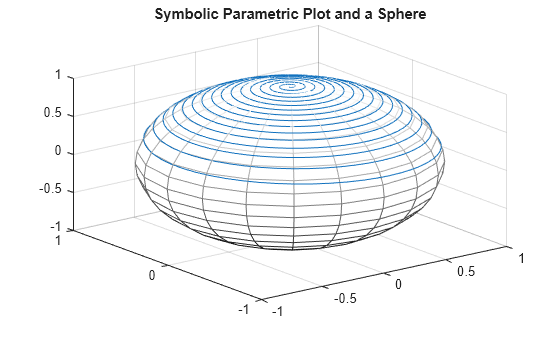
3 次元の数値プロットとシンボリックプロットの結合

MATLAB と Symbolic Math Toolbox のプロット関数を使用して、3 次元のシンボリックプロットと数値プロットを結合します。Symbolic Math Toolbox は以下の 3 次元プロット関数を提供します。

fplot3 - 3 次元パラメーター化ラインプロットを作成。
fsurf - 3 次元表面プロットを作成。
fmesh - 3 次元メッシュプロットを作成。

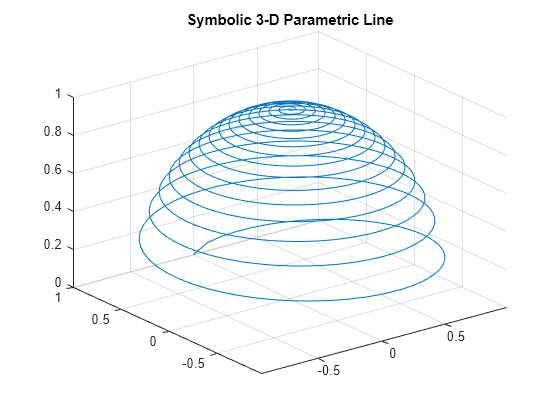
fplot3 を使用してスパイラルプロットを作成し、パラメトリックラインをプロットします。

$\begin{array}{l} x = (1 - t) \sin (100 t) \\ y = (1 - t) \cos (100 t) \\ z = \sqrt{1 - x^{2} - y^{2}} . \end{array}$

syms t
x = (1-t)*sin(100*t);
y = (1-t)*cos(100*t);
z = sqrt(1 - x^2 - y^2);
fplot3(x,y,z,[0 1])
title("Symbolic 3-D Parametric Line")

半径 1、中心 (0,0,0) の球体のプロットを重ね合わせます。sphere を使用して、球体上の点を数値的に求めます。mesh を使用して球体をプロットします。結果として得られたプロットでは、シンボリックのパラメトリックラインが上半球の周囲を包んでいるのがわかります。

hold on
[X,Y,Z] = sphere;
mesh(X,Y,Z)
colormap(gray)
title("Symbolic Parametric Plot and a Sphere")
hold off