bernsteinMatrix
バーンスタイン行列
説明
t がベクトルである場合、B = bernsteinMatrix(n,t)B(i,k+1)= nchoosek(n,k)*t(i)^k*(1-t(i))^(n-k) を満たす length(t) 行 (n+1) 列のバーンスタイン行列 B を返します。ここで、インデックス i は 1 から length(t) まで、インデックス k は 0 から n まで実行されます。
このバーンスタイン行列は、ベジエ行列とも呼ばれています。
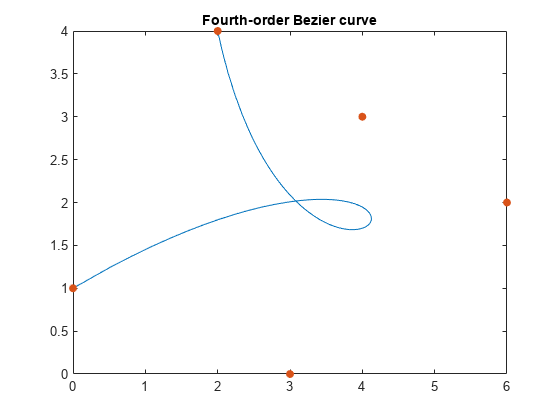
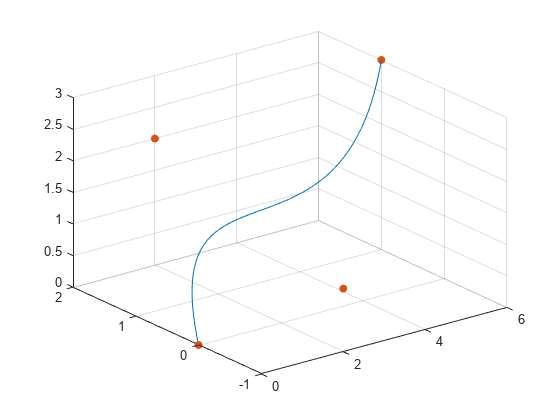
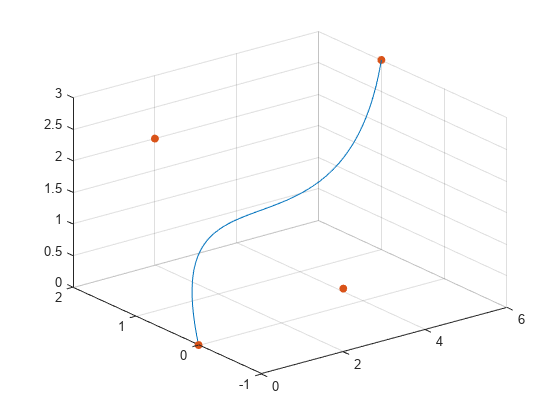
バーンスタイン行列を使って次のようにベジエ曲線を構築します。
bezierCurve = bernsteinMatrix(n, t)*P
P の n+1 行でベジエ曲線の制御点を指定します。たとえば、2 次の 3 次元ベジエ曲線を構築するには、制御点を以下のように指定します。P = [p0x, p0y, p0z; p1x, p1y, p1z; p2x, p2y, p2z]
例
入力引数
出力引数
バージョン履歴
R2013b で導入