多項確率分布オブジェクト
この例では、確率分布オブジェクトを使用した乱数の生成、確率密度関数の計算およびプロット、多項分布の記述統計の計算の方法を示します。
手順 1. 分布パラメーターを定義します。
各結果の確率を含むベクトル p を作成します。結果 1 の確率は 1/2、結果 2 の確率は 1/3、結果 3 の確率は 1/6 です。各実験の試行回数 n は 5、実験の反復数 reps は 8 です。
p = [1/2 1/3 1/6]; n = 5; reps = 8;
手順 2. 多項確率分布オブジェクトを作成します。
Probabilities パラメーターに指定された値 p を使用して多項確率分布オブジェクトを作成します。
pd = makedist('Multinomial','Probabilities',p)
pd =
MultinomialDistribution
Probabilities:
0.5000 0.3333 0.1667
手順 3. 1 つの乱数を生成します。
1 回の試行の結果である多項分布から 1 つの乱数を生成します。
rng('default') % For reproducibility r = random(pd)
r = 2
この試行の結果が結果 2 です。
手順 4. 乱数の行列を生成します。
多項分布から乱数の行列を生成することもできます。この行列は、それぞれ複数の試行を含む複数の実験の結果を報告します。試行回数 n = 5、反復数 reps = 8 の実験の結果を含む行列を生成します。
r = random(pd,reps,n)
r = 8×5
3 3 3 2 1
1 1 2 2 1
3 3 3 1 2
2 3 2 2 2
1 1 1 1 1
1 2 3 2 3
2 1 3 1 1
3 1 2 1 1
結果の行列の各要素は、1 回の試行の結果です。列は各実験の 5 回の試行に対応し、行は 8 回の実験に対応します。たとえば、最初の実験 (最初の行に対応する) では、5 回の試行のうちの 1 回が結果 1、5 回の試行のうちの 1 回が結果 2、5 回の試行のうちの 3 回が結果 3 となります。
手順 5. pdf を計算してプロットします。
分布の pdf を計算します。
x = 1:3; y = pdf(pd,x); bar(x,y) xlabel('Outcome') ylabel('Probability Mass') title('Trinomial Distribution')
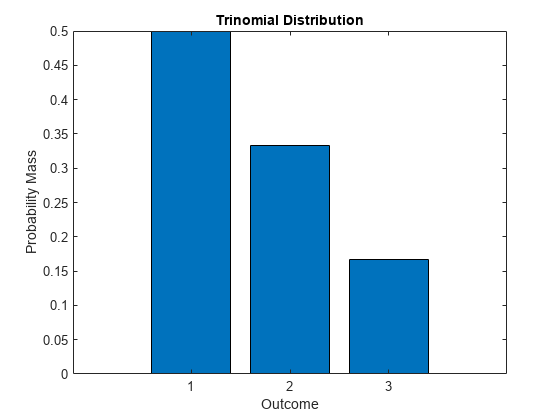
プロットは、 個の起こり得る結果それぞれの確率質量を示しています。この分布では、1、2 または 3 以外の任意の x の pdf 値は 0 です。
手順 6. 記述統計を計算します。
分布の平均、中央値および標準偏差を計算します。
m = mean(pd)
m = 1.6667
med = median(pd)
med = 1
s = std(pd)
s = 0.7454