vartestn
等分散性に関する複数標本検定
構文
説明
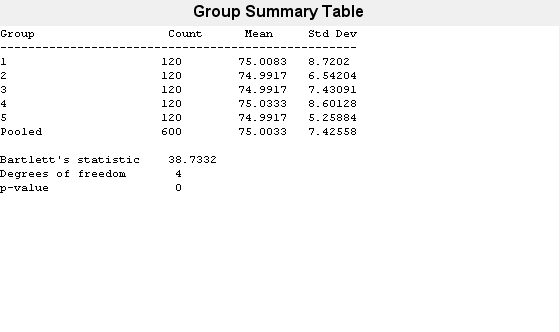
vartestn( は、データ ベクトル x)x の列が同じ分散の正規分布から派生しているという帰無仮説のバートレット検定に対して統計量の概要テーブルと箱ひげ図を返します。対立仮説は、データのすべての列の分散が同じとは限らないとします。
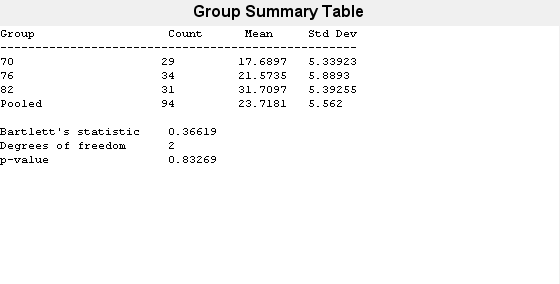
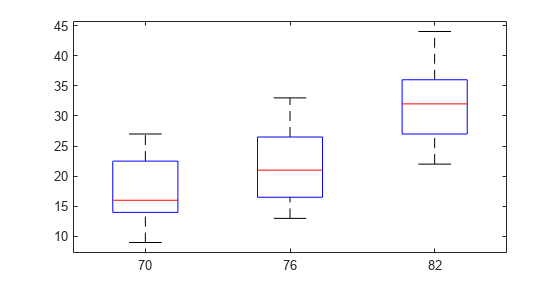
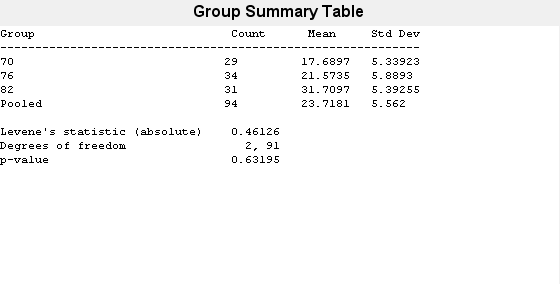
vartestn( は、1 つ以上の名前と値のペア引数で指定された追加オプションを使用して、等しくない分散の検定に対する統計量の概要テーブルと箱ひげ図を返します。たとえば、異なるタイプの仮説検定を指定するか、検定結果の表示設定を変更できます。x,Name,Value)
vartestn( は、1 つ以上の名前と値のペア引数で指定された追加オプションを使用して、等しくない分散の検定に対する統計量の概要テーブルと箱ひげ図を返します。たとえば、異なるタイプの仮説検定を指定するか、検定結果の表示設定を変更できます。x,group,Name,Value)
例
入力引数
名前と値の引数
出力引数
詳細
バージョン履歴
R2006a より前に導入