回帰に NCA を使用するロバスト特徴選択

カスタムなロバスト損失関数を NCA で使用して、外れ値に対してロバストな特徴選択を実行します。

外れ値があるデータの生成

3 つの予測子 (予測子 4、7 および 13) に応答が依存する回帰用の標本データを生成します。

rng(123,'twister') % For reproducibility
n = 200;
X = randn(n,20);
y = cos(X(:,7)) + sin(X(:,4).*X(:,13)) + 0.1*randn(n,1);

外れ値をデータに追加します。

numoutliers = 25;
outlieridx = floor(linspace(10,90,numoutliers));
y(outlieridx) = 5*randn(numoutliers,1);

データをプロットする。

figure
plot(y)

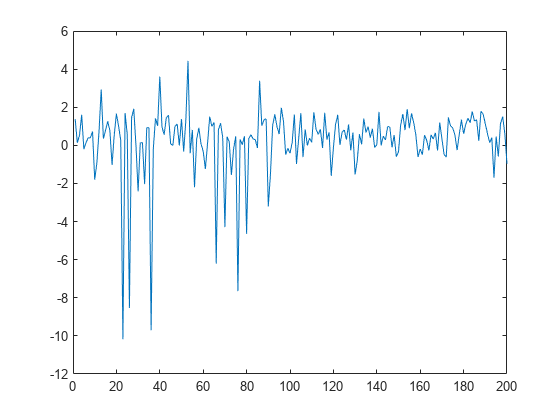
Figure contains an axes object. The axes object contains an object of type line.

非ロバストな損失関数の使用

特徴選択アルゴリズムの性能は、正則化パラメーターの値に大きく依存します。特徴選択での使用に最も適している値になるように正則化パラメーターを調整することをお勧めします。5 分割交差検証を使用して正則化パラメーターを調整します。平均二乗誤差 (MSE) を使用します。

$MSE = \frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - y_{j})}^{2}$

はじめに、データを 5 つの分割に分割します。各分割で、データの 4/5 は学習に、1/5 は検証 (テスト) に使用されます。

cvp = cvpartition(length(y),'kfold',5);
numtestsets = cvp.NumTestSets;

テストするラムダ値を計算し、損失値を格納する配列を作成します。

lambdavals = linspace(0,3,50)*std(y)/length(y);
lossvals = zeros(length(lambdavals),numtestsets);

NCA を実行し、各 $λ$ 値および各分割について損失を計算します。

for i = 1:length(lambdavals)
    for k = 1:numtestsets        
        Xtrain = X(cvp.training(k),:);
        ytrain = y(cvp.training(k),:);
        Xtest = X(cvp.test(k),:);
        ytest = y(cvp.test(k),:);
        
        nca = fsrnca(Xtrain,ytrain,'FitMethod','exact', ...
            'Solver','lbfgs','Verbose',0,'Lambda',lambdavals(i), ...
            'LossFunction','mse');
        
        lossvals(i,k) = loss(nca,Xtest,ytest,'LossFunction','mse');
    end
end

各ラムダ値に対応する平均損失をプロットします。

figure
meanloss = mean(lossvals,2);
plot(lambdavals,meanloss,'ro-')
xlabel('Lambda')
ylabel('Loss (MSE)')
grid on

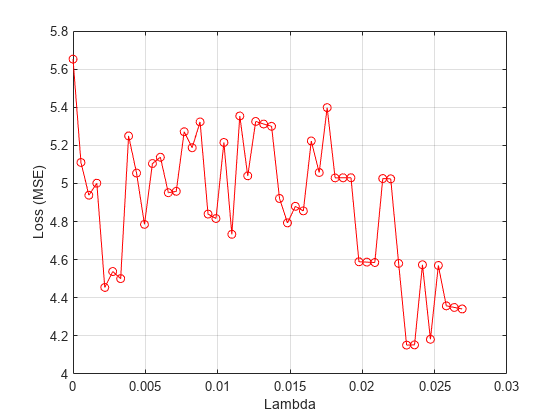
Figure contains an axes object. The axes object with xlabel Lambda, ylabel Loss (MSE) contains an object of type line.

平均損失が最小になる $λ$ の値を求めます。

[~,idx] = min(mean(lossvals,2));
bestlambda = lambdavals(idx)

bestlambda = 0.0231

最良の $λ$ 値および MSE を使用して特徴選択を実行します。

nca = fsrnca(X,y,'FitMethod','exact','Solver','lbfgs', ...
    'Verbose',1,'Lambda',bestlambda,'LossFunction','mse');

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 |  6.414642e+00 |   8.430e-01 |   0.000e+00 |        |   7.117e-01 |   0.000e+00 |   YES  |
|        1 |  6.066100e+00 |   9.952e-01 |   1.264e+00 |    OK  |   3.741e-01 |   1.000e+00 |   YES  |
|        2 |  5.498221e+00 |   4.267e-01 |   4.250e-01 |    OK  |   4.016e-01 |   1.000e+00 |   YES  |
|        3 |  5.108548e+00 |   3.933e-01 |   8.564e-01 |    OK  |   3.599e-01 |   1.000e+00 |   YES  |
|        4 |  4.808456e+00 |   2.505e-01 |   9.352e-01 |    OK  |   8.798e-01 |   1.000e+00 |   YES  |
|        5 |  4.677382e+00 |   2.085e-01 |   6.014e-01 |    OK  |   1.052e+00 |   1.000e+00 |   YES  |
|        6 |  4.487789e+00 |   4.726e-01 |   7.374e-01 |    OK  |   5.593e-01 |   1.000e+00 |   YES  |
|        7 |  4.310099e+00 |   2.484e-01 |   4.253e-01 |    OK  |   3.367e-01 |   1.000e+00 |   YES  |
|        8 |  4.258539e+00 |   3.629e-01 |   4.521e-01 |    OK  |   4.705e-01 |   5.000e-01 |   YES  |
|        9 |  4.175345e+00 |   1.972e-01 |   2.608e-01 |    OK  |   4.018e-01 |   1.000e+00 |   YES  |
|       10 |  4.122340e+00 |   9.169e-02 |   2.947e-01 |    OK  |   3.487e-01 |   1.000e+00 |   YES  |
|       11 |  4.095525e+00 |   9.798e-02 |   2.529e-01 |    OK  |   1.188e+00 |   1.000e+00 |   YES  |
|       12 |  4.059690e+00 |   1.584e-01 |   5.213e-01 |    OK  |   9.930e-01 |   1.000e+00 |   YES  |
|       13 |  4.029208e+00 |   7.411e-02 |   2.076e-01 |    OK  |   4.886e-01 |   1.000e+00 |   YES  |
|       14 |  4.016358e+00 |   1.068e-01 |   2.696e-01 |    OK  |   6.919e-01 |   1.000e+00 |   YES  |
|       15 |  4.004521e+00 |   5.434e-02 |   1.136e-01 |    OK  |   5.647e-01 |   1.000e+00 |   YES  |
|       16 |  3.986929e+00 |   6.158e-02 |   2.993e-01 |    OK  |   1.353e+00 |   1.000e+00 |   YES  |
|       17 |  3.976342e+00 |   4.966e-02 |   2.213e-01 |    OK  |   7.668e-01 |   1.000e+00 |   YES  |
|       18 |  3.966646e+00 |   5.458e-02 |   2.529e-01 |    OK  |   1.988e+00 |   1.000e+00 |   YES  |
|       19 |  3.959586e+00 |   1.046e-01 |   4.169e-01 |    OK  |   1.858e+00 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       20 |  3.953759e+00 |   8.248e-02 |   2.892e-01 |    OK  |   1.040e+00 |   1.000e+00 |   YES  |
|       21 |  3.945475e+00 |   3.119e-02 |   1.698e-01 |    OK  |   1.095e+00 |   1.000e+00 |   YES  |
|       22 |  3.941567e+00 |   2.350e-02 |   1.293e-01 |    OK  |   1.117e+00 |   1.000e+00 |   YES  |
|       23 |  3.939468e+00 |   1.296e-02 |   1.805e-01 |    OK  |   2.287e+00 |   1.000e+00 |   YES  |
|       24 |  3.938662e+00 |   8.591e-03 |   5.955e-02 |    OK  |   1.553e+00 |   1.000e+00 |   YES  |
|       25 |  3.938239e+00 |   6.421e-03 |   5.334e-02 |    OK  |   1.102e+00 |   1.000e+00 |   YES  |
|       26 |  3.938013e+00 |   5.449e-03 |   6.773e-02 |    OK  |   2.085e+00 |   1.000e+00 |   YES  |
|       27 |  3.937896e+00 |   6.226e-03 |   3.368e-02 |    OK  |   7.541e-01 |   1.000e+00 |   YES  |
|       28 |  3.937820e+00 |   2.497e-03 |   2.397e-02 |    OK  |   7.940e-01 |   1.000e+00 |   YES  |
|       29 |  3.937791e+00 |   2.004e-03 |   1.339e-02 |    OK  |   1.863e+00 |   1.000e+00 |   YES  |
|       30 |  3.937784e+00 |   2.448e-03 |   1.265e-02 |    OK  |   9.667e-01 |   1.000e+00 |   YES  |
|       31 |  3.937778e+00 |   6.973e-04 |   2.906e-03 |    OK  |   4.672e-01 |   1.000e+00 |   YES  |
|       32 |  3.937778e+00 |   3.038e-04 |   9.502e-04 |    OK  |   1.060e+00 |   1.000e+00 |   YES  |
|       33 |  3.937777e+00 |   2.327e-04 |   1.069e-03 |    OK  |   1.597e+00 |   1.000e+00 |   YES  |
|       34 |  3.937777e+00 |   1.959e-04 |   1.537e-03 |    OK  |   4.026e+00 |   1.000e+00 |   YES  |
|       35 |  3.937777e+00 |   1.162e-04 |   1.464e-03 |    OK  |   3.418e+00 |   1.000e+00 |   YES  |
|       36 |  3.937777e+00 |   8.353e-05 |   3.660e-04 |    OK  |   7.304e-01 |   5.000e-01 |   YES  |
|       37 |  3.937777e+00 |   1.412e-05 |   1.412e-04 |    OK  |   7.842e-01 |   1.000e+00 |   YES  |
|       38 |  3.937777e+00 |   1.277e-05 |   3.808e-05 |    OK  |   1.021e+00 |   1.000e+00 |   YES  |
|       39 |  3.937777e+00 |   8.614e-06 |   3.698e-05 |    OK  |   2.561e+00 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       40 |  3.937777e+00 |   3.159e-06 |   5.299e-05 |    OK  |   4.331e+00 |   1.000e+00 |   YES  |
|       41 |  3.937777e+00 |   2.657e-06 |   1.080e-05 |    OK  |   7.038e-01 |   5.000e-01 |   YES  |
|       42 |  3.937777e+00 |   7.054e-07 |   7.036e-06 |    OK  |   9.519e-01 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 7.054e-07
              Two norm of the final step     = 7.036e-06, TolX   = 1.000e-06
Relative infinity norm of the final gradient = 7.054e-07, TolFun = 1.000e-06
EXIT: Local minimum found.

選択した特徴量をプロットします。

figure
plot(nca.FeatureWeights,'ro')
grid on
xlabel('Feature index')
ylabel('Feature weight')

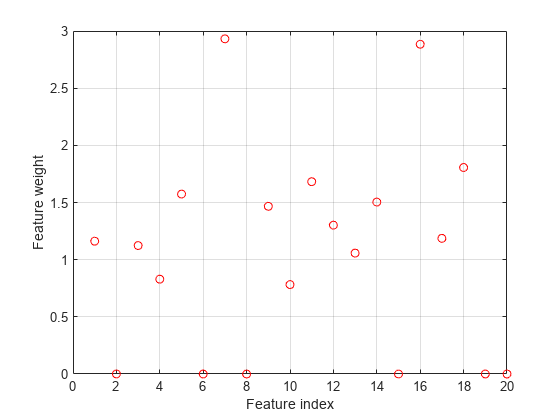
Figure contains an axes object. The axes object with xlabel Feature index, ylabel Feature weight contains a line object which displays its values using only markers.

nca モデルを使用して応答値を予測し、当てはめた (予測した) 応答値と実際の応答値をプロットします。

figure
fitted = predict(nca,X);
plot(y,'r.')
hold on
plot(fitted,'b-')
xlabel('index')
ylabel('Fitted values')

Figure contains an axes object. The axes object with xlabel index, ylabel Fitted values contains 2 objects of type line. One or more of the lines displays its values using only markers

fsrnca は、外れ値を含むデータ内のすべての点を当てはめようとします。この結果、予測子 4、7 および 13 以外の多くの特徴量に非ゼロの重みが割り当てられます。

組み込みロバスト損失関数の使用

同じプロセスを繰り返して正則化パラメーターを調整します。今回は、組み込みの $ϵ$ 許容損失関数を使用します。

$l (y_{i}, y_{j}) = \max (0, | y_{i} - y_{j} | - ϵ)$

$ϵ$ 許容損失関数は平均二乗誤差よりも外れ値に対してロバストです。

lambdavals = linspace(0,3,50)*std(y)/length(y);
cvp = cvpartition(length(y),'kfold',5);
numtestsets = cvp.NumTestSets;
lossvals = zeros(length(lambdavals),numtestsets);

for i = 1:length(lambdavals)
    for k = 1:numtestsets     
        Xtrain = X(cvp.training(k),:);
        ytrain = y(cvp.training(k),:);
        Xtest = X(cvp.test(k),:);
        ytest = y(cvp.test(k),:);
        
        nca = fsrnca(Xtrain,ytrain,'FitMethod','exact', ...
            'Solver','sgd','Verbose',0,'Lambda',lambdavals(i), ...
            'LossFunction','epsiloninsensitive','Epsilon',0.8);
        
        lossvals(i,k) = loss(nca,Xtest,ytest,'LossFunction','mse');
    end
end

使用する $ϵ$ の値はデータによって異なり、最良の値を決定するには交差検証も使用することになります。しかし、 $ϵ$ の値の選択はこの例の範囲外です。この例における $ϵ$ の選択は、主にこの方法のロバスト性を示すためのものです。

各ラムダ値に対応する平均損失をプロットします。

figure
meanloss = mean(lossvals,2);
plot(lambdavals,meanloss,'ro-')
xlabel('Lambda')
ylabel('Loss (MSE)')
grid on

Figure contains an axes object. The axes object with xlabel Lambda, ylabel Loss (MSE) contains an object of type line.

平均損失が最小になるラムダの値を求めます。

[~,idx] = min(mean(lossvals,2));
bestlambda = lambdavals(idx)

bestlambda = 0.0187

$ϵ$ 許容損失関数と最良のラムダの値を使用して近傍成分分析モデルを当てはめます。

nca = fsrnca(X,y,'FitMethod','exact','Solver','sgd', ...
    'Lambda',bestlambda,'LossFunction','epsiloninsensitive','Epsilon',0.8);

選択した特徴量をプロットします。

figure
plot(nca.FeatureWeights,'ro')
grid on
xlabel('Feature index')
ylabel('Feature weight')

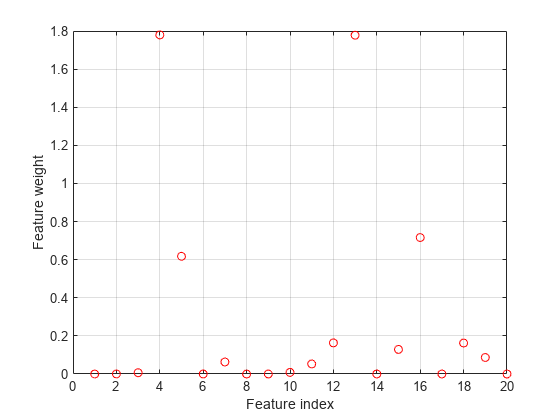
Figure contains an axes object. The axes object with xlabel Feature index, ylabel Feature weight contains a line object which displays its values using only markers.

当てはめた値をプロットします。

figure
fitted = predict(nca,X);
plot(y,'r.')
hold on
plot(fitted,'b-')
xlabel('index')
ylabel('Fitted values')

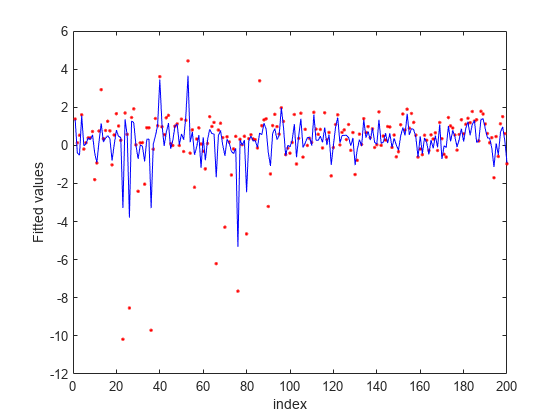
Figure contains an axes object. The axes object with xlabel index, ylabel Fitted values contains 2 objects of type line. One or more of the lines displays its values using only markers

$ϵ$ 許容損失は、外れ値に対するロバスト性が高いようです。関連性があると識別された特徴量の数が MSE より少なくなっています。この当てはめでは、依然として一部の外れ値の影響があることが示されています。

カスタムなロバスト損失関数の使用

外れ値に対してロバストであるカスタムなロバスト損失関数を定義し、回帰用の特徴選択で使用します。

$f (y_{i}, y_{j}) = 1 - \exp (- | y_{i} - y_{j} |)$

customlossFcn = @(yi,yj) 1 - exp(-abs(yi-yj'));

カスタム定義したロバスト損失関数を使用して正則化パラメーターを調整します。

lambdavals = linspace(0,3,50)*std(y)/length(y);
cvp = cvpartition(length(y),'kfold',5);
numtestsets = cvp.NumTestSets;
lossvals = zeros(length(lambdavals),numtestsets);

for i = 1:length(lambdavals)
    for k = 1:numtestsets
        Xtrain = X(cvp.training(k),:);
        ytrain = y(cvp.training(k),:);
        Xtest = X(cvp.test(k),:);
        ytest = y(cvp.test(k),:);
        
        nca = fsrnca(Xtrain,ytrain,'FitMethod','exact', ...
            'Solver','lbfgs','Verbose',0,'Lambda',lambdavals(i), ...
            'LossFunction',customlossFcn);
        
        lossvals(i,k) = loss(nca,Xtest,ytest,'LossFunction','mse');
    end
end

各ラムダ値に対応する平均損失をプロットします。

figure
meanloss = mean(lossvals,2);
plot(lambdavals,meanloss,'ro-')
xlabel('Lambda')
ylabel('Loss (MSE)')
grid on

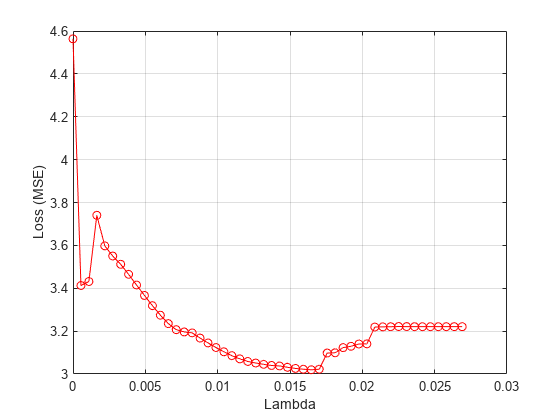
Figure contains an axes object. The axes object with xlabel Lambda, ylabel Loss (MSE) contains an object of type line.

平均損失が最小になる $λ$ の値を求めます。

[~,idx] = min(mean(lossvals,2));
bestlambda = lambdavals(idx)

bestlambda = 0.0165

カスタムなロバスト損失関数と最良の $λ$ の値を使用して特徴選択を実行します。

nca = fsrnca(X,y,'FitMethod','exact','Solver','lbfgs', ...
    'Verbose',1,'Lambda',bestlambda,'LossFunction',customlossFcn);

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 |  8.610073e-01 |   4.921e-02 |   0.000e+00 |        |   1.219e+01 |   0.000e+00 |   YES  |
|        1 |  6.582278e-01 |   2.328e-02 |   1.820e+00 |    OK  |   2.177e+01 |   1.000e+00 |   YES  |
|        2 |  5.706490e-01 |   2.241e-02 |   2.360e+00 |    OK  |   2.541e+01 |   1.000e+00 |   YES  |
|        3 |  5.677090e-01 |   2.666e-02 |   7.583e-01 |    OK  |   1.092e+01 |   1.000e+00 |   YES  |
|        4 |  5.620806e-01 |   5.524e-03 |   3.335e-01 |    OK  |   9.973e+00 |   1.000e+00 |   YES  |
|        5 |  5.616054e-01 |   1.428e-03 |   1.025e-01 |    OK  |   1.736e+01 |   1.000e+00 |   YES  |
|        6 |  5.614779e-01 |   4.446e-04 |   8.350e-02 |    OK  |   2.507e+01 |   1.000e+00 |   YES  |
|        7 |  5.614653e-01 |   4.118e-04 |   2.466e-02 |    OK  |   2.105e+01 |   1.000e+00 |   YES  |
|        8 |  5.614620e-01 |   1.307e-04 |   1.373e-02 |    OK  |   2.002e+01 |   1.000e+00 |   YES  |
|        9 |  5.614615e-01 |   9.318e-05 |   4.128e-03 |    OK  |   3.683e+01 |   1.000e+00 |   YES  |
|       10 |  5.614611e-01 |   4.579e-05 |   8.785e-03 |    OK  |   6.170e+01 |   1.000e+00 |   YES  |
|       11 |  5.614610e-01 |   1.232e-05 |   1.582e-03 |    OK  |   2.000e+01 |   5.000e-01 |   YES  |
|       12 |  5.614610e-01 |   3.174e-06 |   4.742e-04 |    OK  |   2.510e+01 |   1.000e+00 |   YES  |
|       13 |  5.614610e-01 |   7.896e-07 |   1.683e-04 |    OK  |   2.959e+01 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 7.896e-07
              Two norm of the final step     = 1.683e-04, TolX   = 1.000e-06
Relative infinity norm of the final gradient = 7.896e-07, TolFun = 1.000e-06
EXIT: Local minimum found.

選択した特徴量をプロットします。

figure
plot(nca.FeatureWeights,'ro')
grid on
xlabel('Feature index')
ylabel('Feature weight')

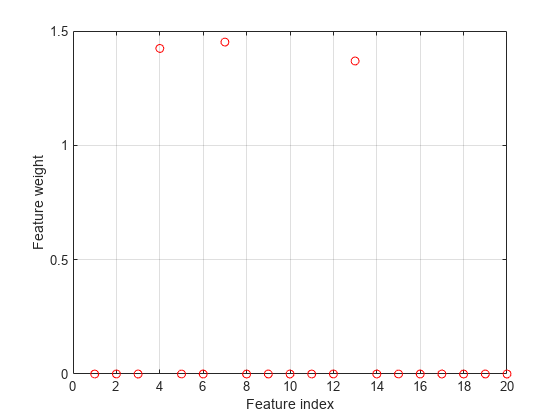
Figure contains an axes object. The axes object with xlabel Feature index, ylabel Feature weight contains a line object which displays its values using only markers.

当てはめた値をプロットします。

figure
fitted = predict(nca,X);
plot(y,'r.')
hold on
plot(fitted,'b-')
xlabel('index')
ylabel('Fitted values')

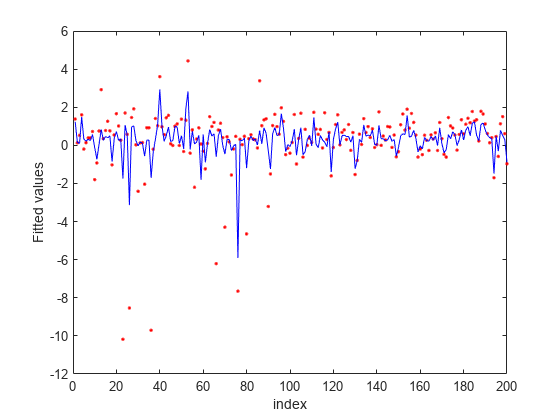
Figure contains an axes object. The axes object with xlabel index, ylabel Fitted values contains 2 objects of type line. One or more of the lines displays its values using only markers

このケースでは、損失が外れ値の影響を受けておらず、結果はほとんどの観測値に基づいています。fsrnca は予測子 4、7 および 13 を関連性がある特徴量として識別しており、他の特徴量は選択していません。

損失関数の選択が結果に影響を与える理由

はじめに、2 つの観測値の差について一連の値の損失関数を計算します。

deltay = linspace(-10,10,1000)';

カスタム損失関数の値を計算します。

customlossvals = customlossFcn(deltay,0);

イプシロン不感応損失関数および値を計算します。

epsinsensitive = @(yi,yj,E) max(0,abs(yi-yj')-E); 
epsinsenvals = epsinsensitive(deltay,0,0.5);

MSE 損失関数および値を計算します。

mse = @(yi,yj) (yi-yj').^2;
msevals = mse(deltay,0);

次に、各損失関数をプロットして、これらの違いおよびこれらが結果に影響を与える理由を調べます。

figure
plot(deltay,customlossvals,'g-',deltay,epsinsenvals,'b-',deltay,msevals,'r-')
xlabel('(yi - yj)')
ylabel('loss(yi,yj)')
legend('customloss','epsiloninsensitive','mse')
ylim([0 20])

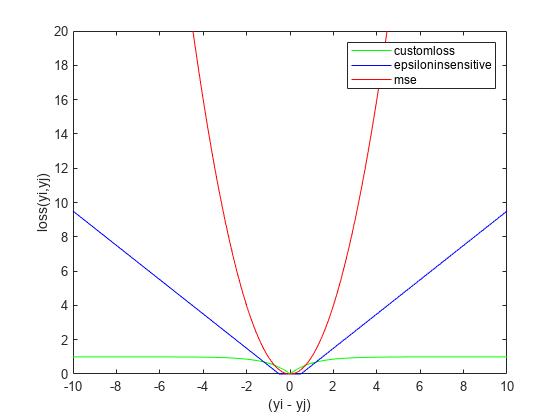
Figure contains an axes object. The axes object with xlabel (yi - yj), ylabel loss(yi,yj) contains 3 objects of type line. These objects represent customloss, epsiloninsensitive, mse.

MSE は、2 つの応答値の差が大きくなると二次関数的に大きくなり、外れ値の影響を大きく受けます。fsrnca がこの損失を最小化しようとすると、より多くの特徴量を関連性があると識別することになります。イプシロン不感応損失は MSE より外れ値に対する耐性が高くなっていますが、結果的には 2 つの観測値の差が大きくなるとそれに比例して大きくなります。ロバスト損失関数は、2 つの観測値の差が大きくなると 1 に近づき、差がさらに大きくなっても値はあまり変化しません。3 つの中で外れ値に対して最もロバストです。

参考

fsrnca | FeatureSelectionNCARegression | refit | predict | loss

回帰に NCA を使用するロバスト特徴選択

外れ値があるデータの生成

非ロバストな損失関数の使用

組み込みロバスト損失関数の使用

カスタムなロバスト損失関数の使用

損失関数の選択が結果に影響を与える理由

参考

関連するトピック