分位点回帰の使用による外れ値の検出
この例では、分位点ランダム フォレストを使用して外れ値を検出する方法を示します。分位点ランダム フォレストは、与えられた に対する の条件付き分布に関して外れ値を検出できます。しかし、この方法では予測子データの外れ値を検出できません。決定木の bag of trees を使用した予測子の外れ値検出については、TreeBagger モデルの OutlierMeasure プロパティを参照してください。
"外れ値" は、データ セット内の他の観測値のほとんどから十分に離れた位置にある観測値なので、異常であると考えられます。異常値の原因には固有変動性や測定ミスなどがあります。外れ値は推定と推論に大きい影響を与えるので、外れ値を検出して、除外するかロバスト分析を検討するかを決定することが重要です。
外れ値の検出を示すため、この例では以下を行います。
不均一分散の非線形モデルからデータを生成し、いくつかの外れ値をシミュレートします。
回帰木の分位点ランダム フォレストを成長させます。
予測子変数の範囲内で条件付き四分位数 (、 および ) と四分位数間範囲 () を推定します。
観測値と "フェンス" (数量 および ) を比較します。 より小さい観測値と より大きい観測値は外れ値です。
データの生成
次のモデルから 500 個の観測値を生成します。
は 0 と の間で一様分布しており、 です。データをテーブルに保存します。
n = 500; rng('default'); % For reproducibility t = randsample(linspace(0,4*pi,1e6),n,true)'; epsilon = randn(n,1).*sqrt((t+0.01)); y = 10 + 3*t + t.*sin(2*t) + epsilon; Tbl = table(t,y);
5 つの観測値をランダムな垂直方向に、応答値の 90% だけ移動します。
numOut = 5; [~,idx] = datasample(Tbl,numOut); Tbl.y(idx) = Tbl.y(idx) + randsample([-1 1],numOut,true)'.*(0.9*Tbl.y(idx));
データの散布図を作成し、外れ値を識別します。
figure; plot(Tbl.t,Tbl.y,'.'); hold on plot(Tbl.t(idx),Tbl.y(idx),'*'); axis tight; ylabel('y'); xlabel('t'); title('Scatter Plot of Data'); legend('Data','Simulated outliers','Location','NorthWest');
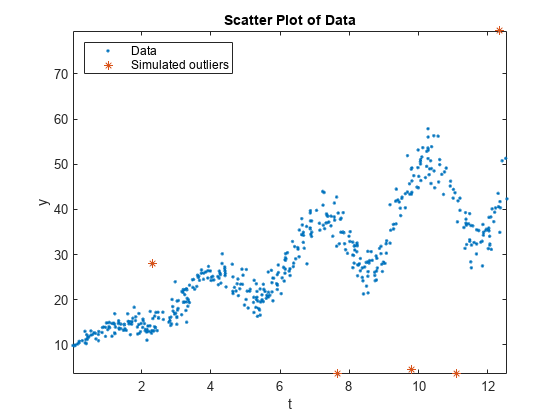
分位点ランダム フォレストの成長
TreeBaggerを使用して 200 本の回帰木の bag of trees を成長させます。
Mdl = TreeBagger(200,Tbl,'y','Method','regression');
Mdl は TreeBagger アンサンブルです。
条件付き四分位数と四分位数間範囲の予測
分位点回帰を使用して、t の範囲内で等間隔に配置されている 50 個の値の条件付き四分位数を推定します。
tau = [0.25 0.5 0.75];
predT = linspace(0,4*pi,50)';
quartiles = quantilePredict(Mdl,predT,'Quantile',tau);quartiles は 500 行 3 列の条件付き四分位数の行列です。行は t の観測値に、列は tau の確率に対応します。
データの散布図上に条件付き平均および中央値応答をプロットします。
meanY = predict(Mdl,predT); plot(predT,[quartiles(:,2) meanY],'LineWidth',2); legend('Data','Simulated outliers','Median response','Mean response',... 'Location','NorthWest'); hold off;
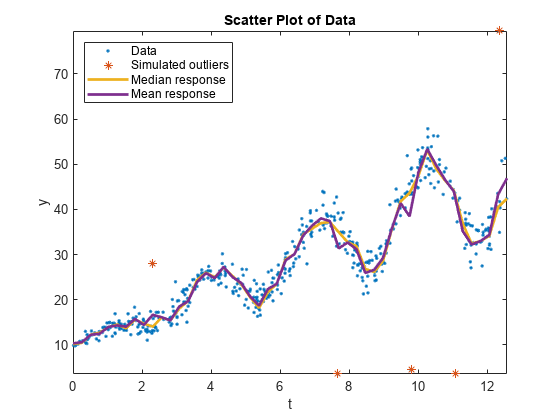
条件付き平均と中央値の曲線は近づいていますが、シミュレートされた外れ値が平均曲線に影響を与える可能性があります。
条件付きの 、 および を計算します。
iqr = quartiles(:,3) - quartiles(:,1); k = 1.5; f1 = quartiles(:,1) - k*iqr; f2 = quartiles(:,3) + k*iqr;
k = 1.5 は、f1 より小さいか f2 より大きいすべての観測値が外れ値であると考えられることを意味しますが、このしきい値は極端な外れ値を明確には区別しません。3 を k にすると極端な外れ値が識別されます。
観測値とフェンスの比較
観測値とフェンスをプロットします。
figure; plot(Tbl.t,Tbl.y,'.'); hold on plot(Tbl.t(idx),Tbl.y(idx),'*'); plot(predT,[f1 f2]); legend('Data','Simulated outliers','F_1','F_2','Location','NorthWest'); axis tight title('Outlier Detection Using Quantile Regression') hold off
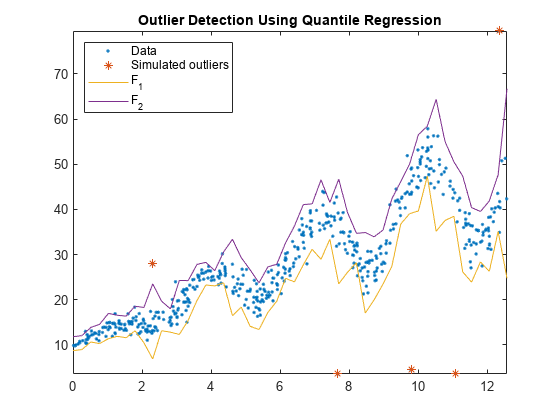
シミュレートされた外れ値はすべて の外部にあり、一部の観測値もこの区間の外部にあります。