mvtcdf
多変量 t 累積分布関数
構文
y = mvtcdf(X,C,DF)
y = mvtcdf(xl,xu,C,DF)
[y,err] = mvtcdf(...)
[...] = mvntdf(...,options)
説明
y = mvtcdf(X,C,DF) は、X の各行で評価される、相関パラメーター C と自由度 DF をもつ多変量 t 分布の累積確率を返します。n 行 d 列の行列 X の行は観測または点に対応し、列は変数または座標に対応します。y は、n 行 1 列のベクトルです。
C は、d x d の対称な正定値行列で、通常は相関行列です。対角要素が 1 でない場合、関数 mvtcdf は、C を相関の形式にスケーリングします。mvtcdf は、X を再スケーリングしません。DF は、スカラーまたは n 要素をもつベクトルです。
多変量 t として分布する乱数ベクトル T の確率として定義される X での多変量 t 累積確率は、X で定義される上限をもつ半無限の矩形範囲、すなわち、Pr{T(1)≤X(1),T(2)≤X(2),...T(d)≤X(d)} に入ります。
y = mvtcdf(xl,xu,C,DF) は、それぞれ xl と xu で定義された上限と下限をもつ矩形全体で評価される、多変量 t 累積確率を返します。
[y,err] = mvtcdf(...) は、y に誤差の推定を返します。二変量分布と三変量分布において、mvtcdf は、参考文献で説明されているように、Genz が開発した手法に基づく t 密度の変換で適応求積法を使用します。これらの場合の既定の設定の絶対許容誤差は、1e-8 です。4 次元以上の場合、mvtcdf は、参考文献で説明されているように Genz と Bretz が開発した手法に基づく準モンテカルロの積分アルゴリズムを使用します。これらの場合の既定の設定の絶対許容誤差は、1e-4 です。
[...] = mvntdf(...,options) は、y の計算に使用される数値積分に対する制御パラメーターを指定します。この引数は、statset の呼び出しで作成されます。statset パラメーターの選択は以下のとおりです。
'TolFun'— 最大絶対許容誤差。既定の設定では、d < 4 の場合1e-8で、d >= 4 の場合1e-4です。'MaxFunEvals'— d ≥ 4 である場合に許容される被積分関数の最大評価回数。既定値は1e7です。d < 4 である場合、'MaxFunEvals'は無視されます。'Display'— 表示出力レベル。選択肢は'off'(既定値)、'iter'、'final'です。'Display'は、d < 4 の場合には無視されます。
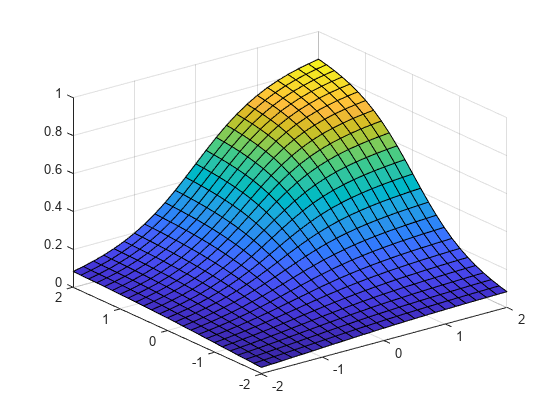
例
参考文献
[1] Genz, A. “Numerical Computation of Rectangular Bivariate and Trivariate Normal and t Probabilities.” Statistics and Computing. Vol. 14, No. 3, 2004, pp. 251–260.
[2] Genz, A., and F. Bretz. “Numerical Computation of Multivariate t Probabilities with Application to Power Calculation of Multiple Contrasts.” Journal of Statistical Computation and Simulation. Vol. 63, 1999, pp. 361–378.
[3] Genz, A., and F. Bretz. “Comparison of Methods for the Computation of Multivariate t Probabilities.” Journal of Computational and Graphical Statistics. Vol. 11, No. 4, 2002, pp. 950–971.
バージョン履歴
R2006a で導入