tall 配列を使用するロジスティック回帰
この例では、ロジスティック回帰および他の手法を使用して tall 配列に対してデータ分析を実行する方法を示します。tall 配列は、大きすぎてコンピューターのメモリに収まらないデータを表します。
実行環境の定義
tall 配列に対する計算を実行する場合、MATLAB® は並列プール (Parallel Computing Toolbox™ がある場合は既定) またはローカルの MATLAB セッションを使用します。Parallel Computing Toolbox がある場合にローカルの MATLAB セッションを使用して例を実行するには、関数 mapreducer を使用してグローバルな実行環境を変更します。
mapreducer(0)
MATLAB へのデータの取得
データがあるフォルダーの場所を参照するデータストアを作成します。データは、単一のファイル、ファイルの集まり、またはフォルダー全体のどれに含まれていてもかまいません。datastore によって NaN 値に置き換えられるようにするため、'NA' 値を欠損データとして扱います。操作する変数のサブセットを選択し、航空会社の名前 (UniqueCarrier) をカテゴリカル変数として含めます。データストアの先頭に tall table を作成します。
ds = datastore('airlinesmall.csv'); ds.TreatAsMissing = 'NA'; ds.SelectedVariableNames = {'DayOfWeek','UniqueCarrier',... 'ArrDelay','DepDelay','Distance'}; ds.SelectedFormats{2} = '%C'; tt = tall(ds); tt.DayOfWeek = categorical(tt.DayOfWeek,1:7,... {'Sun','Mon','Tues','Wed','Thu','Fri','Sat'},'Ordinal',true)
tt =
M×5 tall table
DayOfWeek UniqueCarrier ArrDelay DepDelay Distance
_________ _____________ ________ ________ ________
? ? ? ? ?
? ? ? ? ?
? ? ? ? ?
: : : : :
: : : : :
Preview deferred. Learn more.
フライトの遅れ
フライトが遅れた場合に真になる論理変数を定義することにより、20 分以上遅れたフライトを判別します。この変数をデータの tall table に追加します。まだ評価されていないことに注意してください。この変数のプレビューには、はじめの数行が含まれています。
tt.LateFlight = tt.ArrDelay>=20
tt =
M×6 tall table
DayOfWeek UniqueCarrier ArrDelay DepDelay Distance LateFlight
_________ _____________ ________ ________ ________ __________
? ? ? ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
: : : : : :
: : : : : :
Preview deferred. Learn more.
LateFlight の平均を計算して、フライトの遅れの全体的な比率を求めます。gather を使用して、tall 配列の評価をトリガーし結果をメモリに格納します。
m = mean(tt.LateFlight)
m =
tall double
?
Preview deferred. Learn more.
m = gather(m)
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 2: Completed in 0.46 sec - Pass 2 of 2: Completed in 0.55 sec Evaluation completed in 1.3 sec
m = 0.1580
航空会社別のフライトの遅れ
特定のタイプのフライトに遅れる傾向があるかどうかを調べます。はじめに、特定の航空会社ではフライトが遅れる可能性が高くなるかどうかを調べます。
tt.LateFlight = double(tt.LateFlight); late_by_carrier = gather(grpstats(tt,'UniqueCarrier','mean','DataVar','LateFlight'))
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 1.2 sec Evaluation completed in 1.5 sec
late_by_carrier=29×4 table
GroupLabel UniqueCarrier GroupCount mean_LateFlight
__________ _____________ __________ _______________
{'9E' } 9E 521 0.13436
{'AA' } AA 14930 0.16236
{'AQ' } AQ 154 0.051948
{'AS' } AS 2910 0.16014
{'B6' } B6 806 0.23821
{'CO' } CO 8138 0.16319
{'DH' } DH 696 0.17672
{'DL' } DL 16578 0.15261
{'EA' } EA 920 0.15217
{'EV' } EV 1699 0.21248
{'F9' } F9 335 0.18209
{'FL' } FL 1263 0.19952
{'HA' } HA 273 0.047619
{'HP' } HP 3660 0.13907
{'ML (1)'} ML (1) 69 0.043478
{'MQ' } MQ 3962 0.18778
⋮
航空会社 B6 および EV はフライトの遅れの比率が大きくなっています。航空会社 AQ、ML(1) および HA は、比較的少ないフライト数ですが、遅れる比率は小さくなっています。
曜日別のフライトの遅れ
次に、曜日によってフライトの遅れに傾向があるかどうかを調べます。
late_by_day = gather(grpstats(tt,'DayOfWeek','mean','DataVar','LateFlight'))
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 0.51 sec Evaluation completed in 0.62 sec
late_by_day=7×4 table
GroupLabel DayOfWeek GroupCount mean_LateFlight
__________ _________ __________ _______________
{'Fri' } Fri 15839 0.12899
{'Mon' } Mon 18077 0.14234
{'Sat' } Sat 16958 0.15603
{'Sun' } Sun 18019 0.15117
{'Thu' } Thu 18227 0.18418
{'Tues'} Tues 18163 0.15526
{'Wed' } Wed 18240 0.18399
水曜日と木曜日でフライトの遅れの比率が最も大きくなっており、金曜日で最も小さくなっています。
距離別のフライトの遅れ
フライトの距離によって遅れの傾向があるかどうかを調べます。はじめに、遅れたフライトの飛行距離の密集度を調べ、定刻のフライトと比較します。
ksdensity(tt.Distance(tt.LateFlight==1))
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 2: Completed in 0.44 sec - Pass 2 of 2: Completed in 0.43 sec Evaluation completed in 1.1 sec
hold on
ksdensity(tt.Distance(tt.LateFlight==0))Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 2: Completed in 0.36 sec - Pass 2 of 2: Completed in 0.53 sec Evaluation completed in 1 sec
hold off legend('Late','On time')

飛行距離は、フライトが早いか遅いかによって大きく異なることはありません。しかし、400 マイル前後の距離で、定刻のフライトの密集度がわずかに高くなっているようです。また、2000 マイル前後の距離で、遅延フライトの密度が高くなっています。遅延フライトと定刻のフライトについて、簡単な記述統計をいくつか計算します。
late_by_distance = gather(grpstats(tt,'LateFlight',{'mean' 'std'},'DataVar','Distance'))
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 0.54 sec Evaluation completed in 0.71 sec
late_by_distance=2×5 table
GroupLabel LateFlight GroupCount mean_Distance std_Distance
__________ __________ __________ _____________ ____________
{'0'} 0 1.04e+05 693.14 544.75
{'1'} 1 19519 750.24 574.12
遅延フライトは平均で約 60 マイル長くなっていますが、この値は距離の値の標準偏差では小さな比率を占めるにすぎません。
ロジスティック回帰モデル
連続変数 (Distance など) とカテゴリカル変数 (DayOfWeek など) の両方を使用して確率を予測することにより、フライトが遅れる確率のモデルを構築します。このモデルは、各予測子について個別に観測された以前の結果がまとめて考えた場合にも正しいかどうかを判断するために役立ちます。
glm = fitglm(tt,'LateFlight~Distance+DayOfWeek','Distribution','binomial')
Iteration [1]: 0% completed Iteration [1]: 100% completed Iteration [2]: 0% completed Iteration [2]: 100% completed Iteration [3]: 0% completed Iteration [3]: 100% completed Iteration [4]: 0% completed Iteration [4]: 100% completed Iteration [5]: 0% completed Iteration [5]: 100% completed
glm =
Compact generalized linear regression model:
logit(LateFlight) ~ 1 + DayOfWeek + Distance
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
__________ __________ _______ __________
(Intercept) -1.855 0.023052 -80.469 0
DayOfWeek_Mon -0.072603 0.029798 -2.4365 0.01483
DayOfWeek_Tues 0.026909 0.029239 0.92029 0.35742
DayOfWeek_Wed 0.2359 0.028276 8.343 7.2452e-17
DayOfWeek_Thu 0.23569 0.028282 8.3338 7.8286e-17
DayOfWeek_Fri -0.19285 0.031583 -6.106 1.0213e-09
DayOfWeek_Sat 0.033542 0.029702 1.1293 0.25879
Distance 0.00018373 1.3507e-05 13.602 3.8741e-42
123319 observations, 123311 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 504, p-value = 8.74e-105
このモデルは、以前に観測された結論がやはり正しいことを裏付けています。
水曜日と木曜日の係数は正で、これらの曜日でフライトが遅れる確率が高いことが示されています。金曜日の係数は負なので確率が低いことが示されます。
距離の係数は正なので、飛行距離が長いほど遅れる確率が高くなることがわかります。
これらの係数のすべてで p 値が非常に小さくなっています。これは、多くの観測値が含まれているデータ セットでは大量のデータにより小さい影響を確実に推定できることから、普通に見られます。実際、モデルの不確実性はモデルのパラメーター推定における不確実性より大きくなっています。
モデルによる予測
各曜日および 0 から 3000 マイルまでの距離についてフライトが遅れる確率を予測します。元のテーブル tt の先頭 100 行にインデックスを付けることにより、予測子変数を保持するテーブルを作成します。
x = gather(tt(1:100,{'Distance' 'DayOfWeek'}));Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 0.14 sec Evaluation completed in 0.24 sec
x.Distance = linspace(0,3000)'; x.DayOfWeek(:) = 'Sun'; plot(x.Distance,predict(glm,x)); days = {'Sun' 'Mon' 'Tues' 'Wed' 'Thu' 'Fri' 'Sat'}; hold on for j=2:length(days) x.DayOfWeek(:) = days{j}; plot(x.Distance,predict(glm,x)); end legend(days)
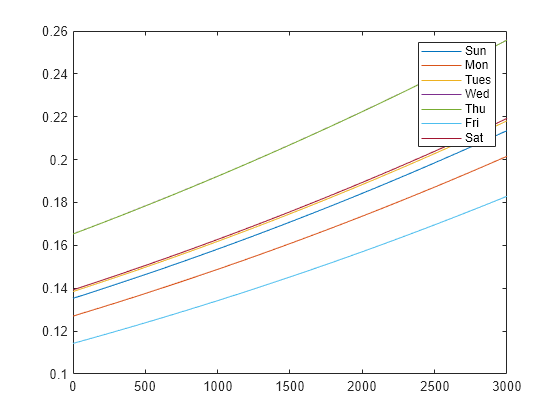
このモデルによると、水曜日または木曜日の 500 マイルのフライトが遅れる確率は約 18% であり、金曜日の約 3000 マイルの場合と同じです。
これらの確率は 50% よりはるかに小さいので、このモデルではこの情報を使用して特定のフライトの遅れを予測することはできないようです。このモデルで予測される遅延確率が 20% 以上のフライトに焦点を当てることによりモデルをさらに調べ、実際の結果と比較します。
C = gather(crosstab(tt.LateFlight,predict(glm,tt)>.20))
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 0.52 sec Evaluation completed in 0.6 sec
C = 2×2
99613 4391
18394 1125
遅れる確率が 20% 以上になると予測されたフライトの中で実際に遅れたのは約 20% (1125/(1125 + 4391)) でした。残りの中で実際に遅れたのは 18394/(18394 + 99613) で 16% 未満でした。