predict
線形混合効果モデルの応答予測
構文
説明
ypred = predict(lme)lme の当てはめに使用される元の予測子の条件付きの予測された応答 ypred を返します。
ypred = predict(___,Name,Value)Name,Value のペアの引数で指定された追加のオプションにより、近似線形混合効果モデル lme から予測応答 ypred のベクトルを返します。
たとえば、信頼水準、同時信頼限界または固定効果のみからの寄与を指定できます。
例
標本データを読み込みます。
load fertilizer.mattable tbl 配列には土壌の種類に基づいて土壌が 3 つのブロックに分けられている分割プロット試験のデータが含まれています。土壌の種類は砂質、シルト、および粘土質です。各ブロックは 5 つのプロットに分割され、5 種類のトマトの苗木 (チェリー、エアルーム、グレープ、枝付き、プラム) がランダムにこれらのプロットに割り当てられます。その後、プロット内のトマトの苗木はサブプロットに分割され、それぞれのサブプロットが 4 つの肥料の中の 1 つにより処置されます。このデータは、シミュレーションされたものです。
table 変数 Tomato、Soil、および Fertilizer をカテゴリカル変数に変換します。
tbl.Tomato = categorical(tbl.Tomato); tbl.Soil = categorical(tbl.Soil); tbl.Fertilizer = categorical(tbl.Fertilizer);
線形混合効果モデルを当てはめます。Fertilizer および Tomato は固定効果変数であり、平均収穫量はブロック (土壌の種類) とブロック内のプロット (土壌の種類の中のトマトの種類) によって独立して変化します。
lme = fitlme(tbl,'Yield ~ Fertilizer * Tomato + (1|Soil) + (1|Soil:Tomato)');元の計画値で応答値を予測します。観測された応答値をもつ最初の 5 つの観測値を表示します。
yhat = predict(lme); [yhat(1:5) tbl.Yield(1:5)]
ans = 5×2
115.4788 104.0000
135.1455 136.0000
152.8121 158.0000
160.4788 174.0000
58.0839 57.0000
標本データを読み込みます。
load carsmallWeight に対する固定効果と、Model_Year でグループ化されたランダム切片で、線形混合効果モデルを当てはめます。まず、データを table に保存します。
tbl = table(MPG,Weight,Model_Year);
lme = fitlme(tbl,'MPG ~ Weight + (1|Model_Year)');データに対する予測された応答を作成します。
yhat = predict(lme,tbl);
元の応答と予測された応答をプロットして、相違点を確認します。それらをモデル年別にグループ化します。
figure() gscatter(Weight,MPG,Model_Year) hold on gscatter(Weight,yhat,Model_Year,[],'o+x') legend('70-data','76-data','82-data','70-pred','76-pred','82-pred') hold off
標本データを読み込み、変数 tbl を表示します。
load fertilizer.mat
tbltbl=60×4 table
Soil Tomato Fertilizer Yield
_________ ____________ __________ _____
{'Sandy'} {'Plum' } 1 104
{'Sandy'} {'Plum' } 2 136
{'Sandy'} {'Plum' } 3 158
{'Sandy'} {'Plum' } 4 174
{'Sandy'} {'Cherry' } 1 57
{'Sandy'} {'Cherry' } 2 86
{'Sandy'} {'Cherry' } 3 89
{'Sandy'} {'Cherry' } 4 98
{'Sandy'} {'Heirloom'} 1 65
{'Sandy'} {'Heirloom'} 2 62
{'Sandy'} {'Heirloom'} 3 113
{'Sandy'} {'Heirloom'} 4 84
{'Sandy'} {'Grape' } 1 54
{'Sandy'} {'Grape' } 2 86
{'Sandy'} {'Grape' } 3 89
{'Sandy'} {'Grape' } 4 115
⋮
table tbl には土壌の種類に基づいて土壌が 3 つのブロックに分けられている分割プロット試験のデータが含まれています。土壌の種類は砂質、シルト、および粘土質です。各ブロックは 5 つのプロットに分割され、5 種類のトマトの苗木 (チェリー、エアルーム、グレープ、枝付き、プラム) がランダムにこれらのプロットに割り当てられます。その後、プロット内のトマトの苗木はサブプロットに分割され、それぞれのサブプロットが 4 つの肥料の中の 1 つにより処置されます。このデータは、シミュレーションされたものです。
table 変数 Tomato、Soil、および Fertilizer をカテゴリカル変数として変換します。
tbl.Tomato = categorical(tbl.Tomato); tbl.Soil = categorical(tbl.Soil); tbl.Fertilizer = categorical(tbl.Fertilizer);
線形混合効果モデルを当てはめます。Fertilizer および Tomato は固定効果変数であり、平均収穫量はブロック (土壌の種類) とブロック内のプロット (土壌の種類の中のトマトの種類) によって独立して変化します。
lme = fitlme(tbl,"Yield ~ Fertilizer * Tomato + (1|Soil) + (1|Soil:Tomato)");計画値をもつ新しい table を作成します。新しいデータセット配列は、モデル lme の近似に使用する元のデータセット配列と同じ変数をもたなければなりません。
tblnew = table(); tblnew.Soil = categorical(["Sandy";"Silty"]); tblnew.Tomato = categorical(["Cherry";"Vine"]); tblnew. Fertilizer = categorical([2;2]);
元の計画点の条件付き応答と限界応答を予測します。
yhatC = predict(lme,tblnew); yhatM = predict(lme,tblnew,Conditional=false); [yhatC yhatM]
ans = 2×2
92.7505 111.6667
87.5891 82.6667
標本データを読み込みます。
load carbigガロンあたりの走行マイル数 (MPG) の線形混合効果モデルを当てはめます。加速度、馬力、気筒数は固定効果で、モデル年によってグループ化される切片と加速度については相関された変量効果の可能性があります。
最初に、線形混合効果モデルを当てはめるための計画行列を準備します。
X = [ones(406,1) Acceleration Horsepower]; Z = [ones(406,1) Acceleration]; Model_Year = nominal(Model_Year); G = Model_Year;
次に、定義した計画行列とグループ化変数で fitlmematrix を使用してモデルを当てはめます。
lme = fitlmematrix(X,MPG,Z,G,'FixedEffectPredictors',.... {'Intercept','Acceleration','Horsepower'},'RandomEffectPredictors',... {{'Intercept','Acceleration'}},'RandomEffectGroups',{'Model_Year'});
応答値を予測する対象データを含む計画行列を作成します。Xnew は X のように 3 つの列をもたなければなりません。最初の列は 1 の列でなければなりません。また、最後の 2 列の値はそれぞれ Acceleration と Horsepower に一致しなければなりません。Znew の 1 列目は 1 の列でなければならず、2 列目には Xnew と同じ Acceleration 値が含まれなければなりません。G の元のグループ化変数はモデル年です。そのため、Gnew にはモデル年の値が含まれなければなりません。Gnew にはノミナル値が含まれていなければなりません。
Xnew = [1,13.5,185; 1,17,205; 1,21.2,193];
Znew = [1,13.5; 1,17; 1,21.2]; % alternatively Znew = Xnew(:,1:2);
Gnew = nominal([73 77 82]);新しい計画行列のデータに対する応答を予測します。
yhat = predict(lme,Xnew,Znew,Gnew)
yhat = 3×1
8.7063
5.4423
12.5384
次に、切片と加速度について変量効果が無相関な線形混合モデルに、同じ手順を繰り返します。最初に、元の変量効果計画と変量効果グループ化変数を変更します。次に、モデルを再度当てはめます。
Z = {ones(406,1),Acceleration};
G = {Model_Year,Model_Year};
lme = fitlmematrix(X,MPG,Z,G,'FixedEffectPredictors',....
{'Intercept','Acceleration','Horsepower'},'RandomEffectPredictors',...
{{'Intercept'},{'Acceleration'}},'RandomEffectGroups',{'Model_Year','Model_Year'});ここで、新しい変量効果計画 Znew およびグループ化変数計画 Gnew を再作成します。これらのどちらかを使用して応答値を予測します。
Znew = {[1;1;1],[13.5;17;21.2]};
MY = nominal([73 77 82]);
Gnew = {MY,MY};新しい計画行列を使用して応答を予測します。
yhat = predict(lme,Xnew,Znew,Gnew)
yhat = 3×1
8.6365
5.9199
12.1247
標本データを読み込みます。
load carbigガロンあたりの走行マイル数 (MPG) の線形混合効果モデルを当てはめます。加速度、馬力、気筒数は固定効果で、モデル年によってグループ化される切片と加速度については相関された変量効果の可能性があります。まず、変数を table に格納します。
tbl = table(MPG,Acceleration,Horsepower,Model_Year);
次に、定義した計画行列とグループ化変数で fitlme を使用してモデルを当てはめます。
lme = fitlme(tbl,'MPG ~ Acceleration + Horsepower + (Acceleration|Model_Year)');新しいデータを作成し、新しい table に格納します。
tblnew = table(); tblnew.Acceleration = linspace(8,25)'; tblnew.Horsepower = linspace(min(Horsepower),max(Horsepower))'; tblnew.Model_Year = repmat(70,100,1);
linspace は、入力値の下限と上限の間で 100 個の等間隔の値を作成します。Model_Year は 70 で固定されています。これは、任意のモデル年について繰り返すことができます。
予測値および 95% の信頼限界 (非同時) を計算およびプロットします。
[ypred,yCI,DF] = predict(lme,tblnew); figure(); h1 = line(tblnew.Acceleration,ypred); hold on; h2 = plot(tblnew.Acceleration,yCI,'g-.');
自由度を表示します。
DF(1)
ans = 389
同時信頼限界を計算およびプロットします。
[ypred,yCI,DF] = predict(lme,tblnew,'Simultaneous',true); h3 = plot(tblnew.Acceleration,yCI,'r--');
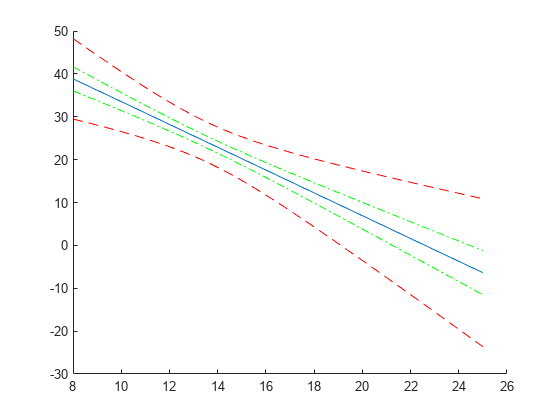
自由度を表示します。
DF
DF = 389
サタースウェイト法を使用して同時信頼限界を計算し、自由度を計算します。
[ypred,yCI,DF] = predict(lme,tblnew,'Simultaneous',true,'DFMethod','satterthwaite'); h4 = plot(tblnew.Acceleration,yCI,'k:'); hold off xlabel('Acceleration') ylabel('Response') ylim([-50,60]) xlim([8,25]) legend([h1,h2(1),h3(1),h4(1)],'Predicted response','95%','95% Sim',... '95% Sim-Satt','Location','Best')
自由度を表示します。
DF
DF = 3.6001
入力引数
名前と値の引数
出力引数
詳細
バージョン履歴
R2013b で導入
