tuneSampler
クラス: HamiltonianSampler
ハミルトニアン モンテカルロ (HMC) サンプラーの調整
構文
tunedSmp = tuneSampler(smp)
[tunedSmp,tuningInfo] = tuneSampler(smp)
[tunedSmp,tuningInfo] = tuneSampler(___,Name,Value)
説明
tunedSmp = tuneSampler(smp)
はじめに、tuneSampler は HMC サンプラー smp の質量ベクトルを調整します。そして、特定の目標採択比率になるようにリープフロッグ法のステップ サイズとステップ数を調整します。
調整済みのサンプラーと drawSamples メソッドを使用してマルコフ連鎖を作成できます。
[ は、追加の調整情報を tunedSmp,tuningInfo] = tuneSampler(smp)tuningInfo で返します。
[ では、1 つ以上の名前と値のペアの引数を使用して追加オプションを指定します。名前と値のペアの引数は、他のすべての入力引数の後で指定します。 tunedSmp,tuningInfo] = tuneSampler(___,Name,Value)
入力引数
調整対象のハミルトニアン モンテカルロ サンプラー。HamiltonianSampler オブジェクトとして指定します。
サンプラーを作成するには、関数 hmcSampler を使用します。
名前と値の引数
オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。
R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。
例: 'StepSizeTuningMethod','dual-averaging','MassVectorTuningMethod','hessian' は、サンプラーのステップ サイズおよび質量ベクトル調整用の指定メソッドを使用して HMC サンプラーを調整します。
調整を開始する初期点。サンプラー smp の StartPoint プロパティと同じ要素数の数値列ベクトルを指定します。
例: 'StartPoint',randn(size(smp.StartPoint))
サンプラーのステップ サイズの調整方法。'StepSizeTuningMethod' と 'dual-averaging' または 'none' から構成されるコンマ区切りのペアとして指定します。
'StepSizeTuningMethod' が 'dual-averaging' に設定された場合、tuneSampler は長さ固定のシミュレーションについて目標採択比率を実現するように HMC サンプラーのリープフロッグ ステップ サイズを調整します。シミュレーションの長さは、ステップ サイズにステップ数を乗算した値です。目標採択比率を指定するには、'TargetAcceptanceRatio' の値を設定します。
シミュレーションの長さを変更するには、何らかの値 a および b について smp.StepSize = a と smp.NumSteps = b を設定します。これにより、シミュレーションの長さが a*b になります。
例: 'StepSizeTuningMethod','none'
サンプラーの質量ベクトルの調整方法。'MassVectorTuningMethod' と次のいずれかの値から構成されるコンマ区切りのペアとして指定します。
| 値 | 説明 |
|---|---|
'iterative-sampling' | 一連の推定質量ベクトルを使用して標本を抽出することにより、連続的な近似で |
'hessian' |
|
'none' | |
例: 'MassVectorTuningMethod','hessian'
ステップ サイズ調整の反復回数。正の整数を指定します。
'StepSizeTuningMethod' の値が 'none' の場合、tuneSampler はステップ サイズを調整しません。
例: 'NumStepSizeTuningIterations',50
マルコフ連鎖の目標採択比率。0 ~ 1 のスカラーを指定します。
tuneSampler は、長さ固定のシミュレーションについて指定された目標採択比率を実現するようにリープフロッグ法のステップ サイズとステップ数を調整します。シミュレーションの長さは、リープフロッグ法のステップ サイズに積分ステップの回数を乗算した値です。
'StepSizeTuningMethod' の値が 'none' の場合、tuneSampler はステップ サイズを調整しません。
シミュレーションの長さを変更するには、何らかの値 a および b について smp.StepSize = a と smp.NumSteps = b を設定します。これにより、シミュレーションの長さが a*b になります。
例: 'TargetAcceptanceRatio',0.55
ステップ サイズ調整時に許容される、リープフロッグの最大ステップ数。正の整数を指定します。
'StepSizeTuningMethod' の値が 'none' の場合、tuneSampler はステップ サイズを調整しません。
例: 'NumStepsLimit',1000
サンプラー調整時のコマンド ウィンドウ出力の詳細レベル。非負の整数を指定します。
値が
0に設定された場合、tuneSamplerは調整の詳細を表示しません。値が
1に設定された場合、tuneSamplerはステップ サイズの調整の詳細を表示します。値が
2以上に設定された場合、tuneSamplerはステップ サイズと質量ベクトルの調整の詳細を表示します。
| 見出し | 説明 |
|---|---|
ITER | 反復回数。 |
LOG PDF | 現在の反復における対数確率密度。 |
STEP SIZE | 現在の反復におけるリープフロッグ法のステップ サイズ。 |
NUM STEPS | 現在の反復におけるリープフロッグ法のステップ数。 |
ACC RATIO | 採択比率、つまり採択された提案の割合。 |
DIVERGENT | リープフロッグ反復で |
例: 'VerbosityLevel',1
詳細出力の頻度。正の整数を指定します。
'VerbosityLevel' の値が正の整数である場合、tuneSampler は 'NumPrint' 回の反復ごとに調整の詳細を出力します。
例: 'NumPrint',50
出力引数
調整されたハミルトニアン モンテカルロ サンプラー。HamiltonianSampler オブジェクトとして返されます。
調整情報。次のフィールドがある構造体として返されます。
| フィールド | 説明 |
|---|---|
MassVector | 調整された質量ベクトル |
StepSize | 調整されたリープフロッグ ステップ サイズ |
NumSteps | 調整されたリープフロッグ法のステップ数の値 |
MassVectorTuningInfo | 質量ベクトルの調整に関する追加情報が含まれている構造体 |
StepSizeTuningInfo | ステップ サイズの調整に関する追加情報が含まれている構造体 |
'iterative-sampling' 法を使用して質量ベクトルを調整した場合、MassVectorTuningInfo には次のフィールドが含まれます。
| フィールド | 説明 |
|---|---|
MassVector | 調整された質量ベクトル |
IterativeSamplingMassVectorProfile | K 回の反復で使用された質量ベクトルが格納されている P 行 K 列の行列。P はサンプリング変数の個数 |
IterativeSamplingNumSamples | K 回の反復のそれぞれで抽出された標本の個数が格納されている K 行 1 列のベクトル |
'hessian' 法を使用して質量ベクトルを調整した場合、MassVectorTuningInfo には次のフィールドが含まれます。
| フィールド | 説明 |
|---|---|
MassVector | 調整された質量ベクトル |
NegativeDiagonalHessian | 調整開始点における |
HessianPoint | ヘッシアンを評価した点 |
MassVectorTuningMethod の値が 'none' の場合、MassVectorTuningInfo は空になります。
'dual-averaging' 法を使用してステップ サイズを調整した場合、StepSizeTuningInfo には次のフィールドが含まれます。
| フィールド | 説明 |
|---|---|
StepSize | 調整されたステップ サイズ |
NumSteps | 調整されたステップ数の値 |
StepSizeProfile | 各調整反復におけるステップ サイズが格納されている列ベクトル |
AcceptanceRatio | 調整で達成された最終的な採択比率 |
ステップ サイズを調整しなかった場合、StepSizeTuningInfo は空になります。
データ型: struct
例
ハミルトニアン モンテカルロ (HMC) サンプラーのパラメーターを調整します。
サンプリングするパラメーターの個数とその平均を定義します。
NumParams = 9; means = [1:NumParams]'; standevs = 1;
はじめに、多変量正規対数確率密度およびその勾配を返す関数 normalDistGrad を MATLAB® パス上に保存します (normalDistGrad はこの例の終わりで定義します)。次に、引数を指定してこの関数を呼び出し、関数 hmcSampler の入力引数 logpdf を定義します。
logpdf = @(theta)normalDistGrad(theta,means,standevs);
開始点を選択し、HMC サンプラーを作成します。
startpoint = randn(NumParams,1); smp = hmcSampler(logpdf,startpoint);
サンプリングの効率化には、サンプラーのパラメーターに適切な値を選択することが重要です。適切な値を求めるための最適な方法として、tuneSampler を使用してパラメーター MassVector、StepSize および NumSteps を自動的に調整します。このメソッドは以下を行います。
1.サンプラーの MassVector を調整する。
2.特定の採択比率を達成するため、長さ固定のシミュレーションについて StepSize と NumSteps を調整する。多くの場合、既定のターゲット採択比率である 0.65 が適しています。
[smp,info] = tuneSampler(smp,'NumStepSizeTuningIterations',50,'VerbosityLevel',1,'NumPrint',10);
o Tuning mass vector using method: iterative-sampling Finished mass vector tuning iteration 1 of 5. Finished mass vector tuning iteration 2 of 5. Finished mass vector tuning iteration 3 of 5. Finished mass vector tuning iteration 4 of 5. Finished mass vector tuning iteration 5 of 5. o Tuning step size using method: dual-averaging. Target acceptance ratio = 0.65 o Initial step size for dual-averaging = 2 |==================================================================================| | ITER | LOG PDF | STEP SIZE | NUM STEPS | ACC RATIO | DIVERGENT | |==================================================================================| | 10 | -1.710457e+01 | 1.193e+00 | 4 | 5.000e-01 | 0 | | 20 | -9.152514e+00 | 9.527e-01 | 5 | 5.500e-01 | 0 | | 30 | -1.068923e+01 | 8.856e-01 | 6 | 5.333e-01 | 0 | | 40 | -1.290816e+01 | 8.506e-01 | 6 | 5.750e-01 | 0 | | 50 | -1.770386e+01 | 8.581e-01 | 6 | 6.000e-01 | 0 |
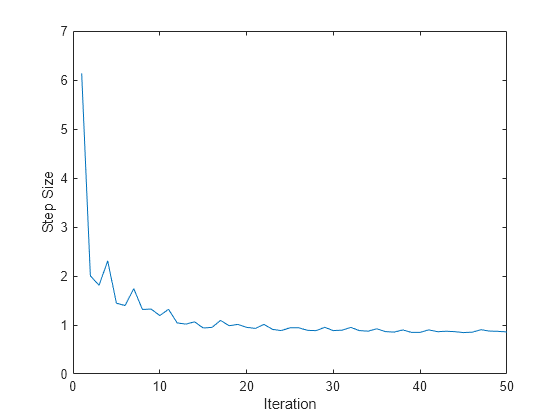
ステップ サイズの調整が収束したことを確認するため、調整時のステップ サイズの変化をプロットします。達成された採択比率を表示します。
figure; plot(info.StepSizeTuningInfo.StepSizeProfile); xlabel('Iteration'); ylabel('Step Size');
accratio = info.StepSizeTuningInfo.AcceptanceRatio
accratio = 0.6000
関数 normalDistGrad は、startpoint と同じ長さの列ベクトルまたはスカラーとして指定された Mu に格納されている平均および Sigma に格納されている標準偏差を使用して、多変量正規確率密度の対数を返します。2 番目の出力引数は、対応する勾配です。
function [lpdf,glpdf] = normalDistGrad(X,Mu,Sigma) Z = (X - Mu)./Sigma; lpdf = sum(-log(Sigma) - .5*log(2*pi) - .5*(Z.^2)); glpdf = -Z./Sigma; end
ヒント
関数
hmcSamplerを使用して HMC サンプラーを作成した後でHamiltonianSamplerクラスのメソッドを使用して、MAP (最大事後確率) 点推定の計算、サンプラーの調整、標本の抽出、収束診断のチェックを行うことができます。このワークフローの例については、ハミルトニアン モンテカルロの使用によるベイズ線形回帰を参照してください。
バージョン履歴
R2017a で導入
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)