Main Content

ハミルトニアン モンテカルロの使用によるベイズ線形回帰

スクリプトを開く

この例では、ハミルトニアン モンテカルロ (HMC) サンプラーを使用して線形回帰モデルに対してベイズ推論を実行する方法を示します。

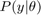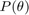ベイズ パラメーター推定の目標は、モデル パラメーターに関する事前知識を組み入れて統計モデルを分析することです。自由パラメーター $\theta$ の事後分布は、次のベイズの定理を使用して、尤度関数 $P(y | \theta)$ と事前分布 $P(\theta)$ を結合します。

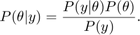
$$ P(\theta | y) = \frac{P(y | \theta) P(\theta)}{P(y)}.$$

通常、事後分布を集計する最適な方法は、モンテカルロ法を使用してその分布から標本を取得することです。これらの標本を使用して、周辺事後分布と派生統計 (事後平均、中央値、標準偏差など) を推定できます。HMC は勾配に基づくマルコフ連鎖モンテカルロ サンプラーであり、特に中次元問題と高次元問題の場合に、標準的なサンプラーより効率的になる可能性があります。

線形回帰モデル

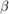自由パラメーターとしてデータ分布の切片 $\alpha$、線形係数 $\beta$ (列ベクトル) およびノイズ分散 $\sigma^2$ をもつ線形回帰モデルを分析します。各データ点には独立したガウス分布があると仮定します。

$$ y_i|\theta \sim \mathcal{N}(\mu_i(\theta), \sigma^2). $$

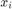ガウス分布の平均 $\mu_i$ を予測子 $x_i$ とモデル パラメーターの関数としてモデル化します。

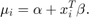
$$\mu_i = \alpha + x_i^T \beta.$$

ベイズ分析では、事前分布をすべての自由パラメーターに割り当てる必要もあります。独立したガウス事前分布を切片と線形係数に割り当てます。

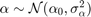$\alpha \sim \mathcal{N}(\alpha_0, \sigma_\alpha^2)$,

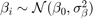$\beta_i \sim \mathcal{N}(\beta_{0}, \sigma_{\beta}^2)$.

HMC を使用するには、すべてのサンプリング変数が制約なしでなければなりません。つまり、すべての実数パラメーター値について事後密度とその勾配が明確に定義されていなければなりません。ある区間に制約されるパラメーターがある場合、このパラメーターを非有界のパラメーターに変換しなければなりません。確率を保持するには、事前分布を対応するヤコビ因子で乗算しなければなりません。また、事後密度の勾配を計算するときに、この因子を考慮します。

ノイズ分散は、正にしかならない (平方の) スケール パラメーターです。したがって、その対数を自由パラメーターとして考える方が容易であり自然です。これは非有界です。正規事前分布をノイズ分散の対数に割り当てます。

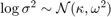$\log \sigma^2 \sim \mathcal{N}(\kappa, \omega^2)$.

自由パラメーター 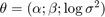$\theta = (\alpha; \beta; \log \sigma^2)$ の事後密度の対数を次のように記述します。

$$\log P(\theta | y) = \mathrm{const.} + \log P(y | \theta) + \log
P(\theta).$$

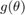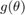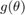定数項を無視し、最後の 2 つの項の和を $g(\theta)$ と呼びます。HMC を使用するため、任意の値の $\theta$ について $g(\theta)$ とその勾配 ${\partial g}/{\partial \theta}$ を評価する関数ハンドルを作成します。$g(\theta)$ の計算に使用する関数は、スクリプトの最後に配置します。

データ セットの作成

切片、線形係数 Beta およびノイズ標準偏差について、真のパラメーター値を定義します。真のパラメーター値がわかると、HMC サンプラーの出力と比較できます。応答に影響を与えるのは 1 番目の予測子のみです。

NumPredictors = 2;

trueIntercept = 2;
trueBeta = [3;0];
trueNoiseSigma = 1;

これらのパラメーター値を使用して、2 つの予測子の乱数値で正規分布している標本データ セットを作成します。

NumData = 100;
rng('default') %For reproducibility
X = rand(NumData,NumPredictors);
mu = X*trueBeta + trueIntercept;
y = normrnd(mu,trueNoiseSigma);

事後確率密度の定義

ガウス事前分布の平均と標準偏差を選択します。

InterceptPriorMean = 0;
InterceptPriorSigma = 10;
BetaPriorMean = 0;
BetaPriorSigma = 10;
LogNoiseVarianceMean = 0;
LogNoiseVarianceSigma = 2;

関数 logPosterior を MATLAB® パスに保存します。この関数は、事前分布と尤度の積の対数、およびこの対数の勾配を返します。関数 logPosterior の定義は、この例の終わりで行います。次に、引数を指定してこの関数を呼び出し、関数 hmcSampler の入力引数 logpdf を定義します。

logpdf = @(Parameters)logPosterior(Parameters,X,y, ...
    InterceptPriorMean,InterceptPriorSigma, ...
    BetaPriorMean,BetaPriorSigma, ...
    LogNoiseVarianceMean,LogNoiseVarianceSigma);

HMC サンプラーの作成

サンプリングを開始する初期点を定義してから、HamiltonianSampler オブジェクトとしてハミルトニアン サンプラーを作成するため、関数 hmcSampler を呼び出します。サンプラーのプロパティを表示します。

Intercept = randn;
Beta = randn(NumPredictors,1);
LogNoiseVariance = randn;
startpoint = [Intercept;Beta;LogNoiseVariance];
smp = hmcSampler(logpdf,startpoint,'NumSteps',50);

smp

smp = 

  HamiltonianSampler with properties:

                  StepSize: 0.1000
                  NumSteps: 50
                MassVector: [4x1 double]
              JitterMethod: 'jitter-both'
      StepSizeTuningMethod: 'dual-averaging'
    MassVectorTuningMethod: 'iterative-sampling'
                    LogPDF: [function_handle]
             VariableNames: {4x1 cell}
                StartPoint: [4x1 double]

MAP 点の推定

事後密度の MAP (最大事後) 点を推定します。サンプリングはどの点からでも開始できますが、多くの場合、MAP 点を推定し、サンプラーの調整と標本の抽出を行うための開始点として使用する方が効率的です。MAP 点を推定して表示します。'VerbosityLevel' の値を 1 に設定すると、より多くの情報を最適化時に表示できます。

[MAPpars,fitInfo] = estimateMAP(smp,'VerbosityLevel',0);
MAPIntercept = MAPpars(1)
MAPBeta = MAPpars(2:end-1)
MAPLogNoiseVariance = MAPpars(end)

MAPIntercept =

    2.3857


MAPBeta =

    2.5495
   -0.4508


MAPLogNoiseVariance =

   -0.1007

最適化が局所的な最適解に収束したことをチェックするため、fitInfo.Objective フィールドをプロットします。このフィールドには、関数最適化の各反復における負の対数密度の値が含まれています。最終的な値はすべてほぼ同じ、つまり最適化は収束しています。

plot(fitInfo.Iteration,fitInfo.Objective,'ro-');
xlabel('Iteration');
ylabel('Negative log density');

サンプラーの調整

サンプリングの効率化には、サンプラーのパラメーターに適切な値を選択することが重要です。適切な値を見つけるための最適な方法として、tuneSampler メソッドを使用してパラメーター MassVector、StepSize および NumSteps を自動的に調整します。このメソッドを使用して、以下を行います。

1.サンプラーの MassVector を調整する。

2.一定の採択比率を達成するため、長さ固定のシミュレーションについて StepSize と NumSteps を調整する。多くの場合、既定のターゲット採択比率である 0.65 が適しています。

より効率的に調整を行うため、推定された MAP 点で調整を開始します。

[smp,tuneinfo] = tuneSampler(smp,'Start',MAPpars);

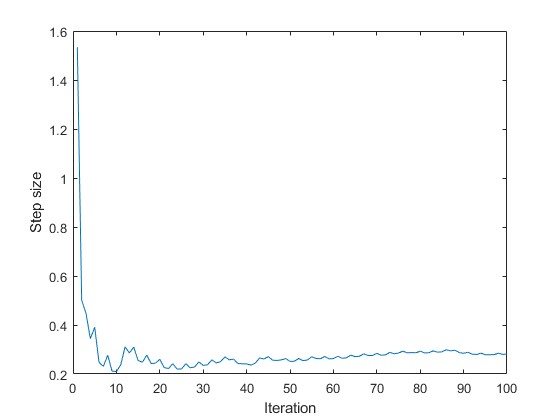
ステップ サイズの調整が収束したことを確認するため、調整時のステップ サイズの変化をプロットします。達成された採択比率を表示します。

figure;
plot(tuneinfo.StepSizeTuningInfo.StepSizeProfile);
xlabel('Iteration');
ylabel('Step size');

accratio = tuneinfo.StepSizeTuningInfo.AcceptanceRatio

accratio =

    0.6700

標本の抽出

いくつかの独立した連鎖を使用して、事後密度から標本を抽出します。各連鎖について異なる初期点を選択します。これらは、推定された MAP 点の周辺でランダムに分布しています。マルコフ連鎖の先頭から破棄するバーンイン標本の数と、バーンイン後に生成する標本の数を指定します。

1 番目の連鎖についてサンプリング時の詳細を出力するように 'VerbosityLevel' の値を設定します。

NumChains = 4;
chains = cell(NumChains,1);
Burnin = 500;
NumSamples = 1000;
for c = 1:NumChains
    if (c == 1)
        level = 1;
    else
        level = 0;
    end
    chains{c} = drawSamples(smp,'Start',MAPpars + randn(size(MAPpars)), ...
        'Burnin',Burnin,'NumSamples',NumSamples, ...
        'VerbosityLevel',level,'NumPrint',300);
end


|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      300 | -1.490356e+02 |   2.617e-01 |          11 |   9.467e-01 |           0 |
|      600 | -1.493478e+02 |   2.199e-02 |           3 |   9.367e-01 |           0 |
|      900 | -1.509868e+02 |   2.244e-01 |           5 |   9.422e-01 |           0 |
|     1200 | -1.493611e+02 |   1.166e-01 |          15 |   9.300e-01 |           0 |
|     1500 | -1.488397e+02 |   2.617e-01 |          11 |   9.320e-01 |           0 |

収束診断の確認

diagnostics メソッドを使用して、標準的な MCMC 診断を計算します。このメソッドでは、各サンプリング パラメーターについて、すべての連鎖を使用して次の統計量を計算します。

  • 事後平均推定値 (Mean)

  • 事後平均推定値の標準偏差である、モンテカルロ標準誤差の推定値 (MCSE)

  • 事後標準偏差の推定値 (SD)

  • 周辺事後分布の 5 番目と 95 番目の分位数の推定値 (Q5 と Q95)

  • 事後平均推定値の有効な標本サイズ (ESS)

  • Gelman-Rubin 収束統計量 (RHat)。目安として、RHat の値が 1.1 未満の場合は、目的の分布に連鎖が収束したと解釈できます。RHat が 1.1 より大きい変数がある場合は、drawSamples メソッドを使用して、より多くの標本を抽出するようにします。

診断表と、この例の最初で定義したサンプリング パラメーターの真の値を表示します。このデータ セットでは事前分布の情報が無いため、真の値は 5 番目と 95 番目の分位数の間 (または近く) にあります。

diags = diagnostics(smp,chains)
truePars = [trueIntercept;trueBeta;log(trueNoiseSigma^2)]

diags =

  4x8 table

     Name       Mean         MCSE         SD          Q5         Q95       ESS       RHat 
    ______    _________    _________    _______    ________    _______    ______    ______

    {'x1'}       2.3792    0.0055101    0.27821      1.9116     2.8372    2549.3    1.0009
    {'x2'}       2.5533    0.0062076    0.32836      2.0223     3.0959    2798.1    1.0004
    {'x3'}     -0.43983    0.0065001    0.34398     -1.0192    0.12916    2800.5    1.0001
    {'x4'}    -0.063367    0.0028645    0.14159    -0.28853     0.1838    2443.3    1.0004


truePars =

     2
     3
     0
     0

標本の可視化

収束や混合などの問題を調べて、抽出した標本が対象の分布からの無作為な実現の妥当な集合を表しているかどうかを判断します。出力を確認するため、1 番目の連鎖を使用して標本のトレース プロットをプロットします。

drawSamples メソッドでは、サンプリングの開始点による影響を抑えるため、マルコフ連鎖の先頭からバーンイン標本を破棄します。さらに、トレース プロットは、目に見える長周期の相関が標本間にない高周波ノイズのように見えます。この挙動は、連鎖が十分に混合されていることを示します。

figure;
subplot(2,2,1);
plot(chains{1}(:,1));
title(sprintf('Intercept, Chain 1'));
for p = 2:1+NumPredictors
    subplot(2,2,p);
    plot(chains{1}(:,p));
    title(sprintf('Beta(%d), Chain 1',p-1));
end
subplot(2,2,4);
plot(chains{1}(:,end));
title(sprintf('LogNoiseVariance, Chain 1'));

連鎖を 1 つの行列に結合し、散布図とヒストグラムを作成して、1 次元および 2 次元の周辺事後分布を可視化します。

concatenatedSamples = vertcat(chains{:});
figure;
plotmatrix(concatenatedSamples);
title('All Chains Combined');

事後分布を計算する関数

関数 logPosterior は、線形モデルについて正規尤度と正規事前分布の積の対数を返します。入力引数 Parameter の形式は [Intercept;Beta;LogNoiseVariance] です。X と Y には、それぞれ予測子および応答の値が含まれています。

関数 normalPrior は、P と同じ長さの列ベクトルまたはスカラーとして指定される、平均 Mu および標準偏差 Sigma をもつ多変量正規確率密度の対数を返します。2 番目の出力引数は、対応する勾配です。

function [logpdf, gradlogpdf] = logPosterior(Parameters,X,Y, ...
    InterceptPriorMean,InterceptPriorSigma, ...
    BetaPriorMean,BetaPriorSigma, ...
    LogNoiseVarianceMean,LogNoiseVarianceSigma)


% Unpack the parameter vector
Intercept        = Parameters(1);
Beta             = Parameters(2:end-1);
LogNoiseVariance = Parameters(end);
% Compute the log likelihood and its gradient
Sigma                   = sqrt(exp(LogNoiseVariance));
Mu                      = X*Beta + Intercept;
Z                       = (Y - Mu)/Sigma;
loglik                  = sum(-log(Sigma) - .5*log(2*pi) - .5*Z.^2);
gradIntercept1          = sum(Z/Sigma);
gradBeta1               = X'*Z/Sigma;
gradLogNoiseVariance1	= sum(-.5 + .5*(Z.^2));
% Compute log priors and gradients
[LPIntercept, gradIntercept2]           = normalPrior(Intercept,InterceptPriorMean,InterceptPriorSigma);
[LPBeta, gradBeta2]                     = normalPrior(Beta,BetaPriorMean,BetaPriorSigma);
[LPLogNoiseVar, gradLogNoiseVariance2]  = normalPrior(LogNoiseVariance,LogNoiseVarianceMean,LogNoiseVarianceSigma);
logprior                                = LPIntercept + LPBeta + LPLogNoiseVar;
% Return the log posterior and its gradient
logpdf               = loglik + logprior;
gradIntercept        = gradIntercept1 + gradIntercept2;
gradBeta             = gradBeta1 + gradBeta2;
gradLogNoiseVariance = gradLogNoiseVariance1 + gradLogNoiseVariance2;
gradlogpdf           = [gradIntercept;gradBeta;gradLogNoiseVariance];
end

function [logpdf,gradlogpdf] = normalPrior(P,Mu,Sigma)
Z          = (P - Mu)./Sigma;
logpdf     = sum(-log(Sigma) - .5*log(2*pi) - .5*(Z.^2));
gradlogpdf = -Z./Sigma;
end

参考

関数

クラス