drawSamples

クラス: HamiltonianSampler

ハミルトニアン モンテカルロ (HMC) の使用によるマルコフ連鎖の生成

構文

chain = drawSamples(smp)
[chain,endpoint,accratio] = drawSamples(smp)
[chain,endpoint,accratio] = drawSamples(___,Name,Value)


説明

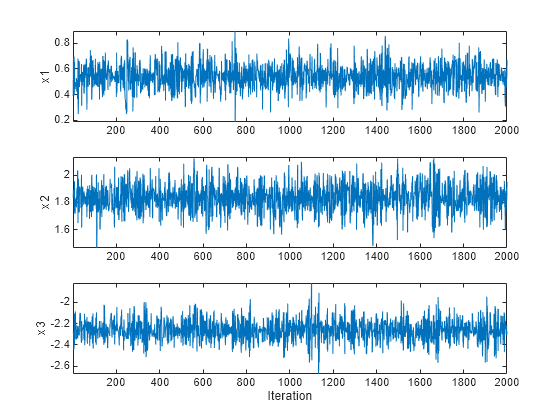
chain = drawSamples(smp) は、ハミルトニアン モンテカルロ サンプラー smp を使用して標本を抽出することによりマルコフ連鎖を生成します。

[chain,endpoint,accratio] = drawSamples(smp) は、マルコフ連鎖の最終状態を endpoint で、採択された提案の割合を accratio で返します。

[chain,endpoint,accratio] = drawSamples(___,Name,Value) では、1 つ以上の名前と値のペアの引数を使用して追加オプションを指定します。名前と値のペアの引数は、他のすべての入力引数の後で指定します。

入力引数

smp — ハミルトニアン モンテカルロ サンプラー

HamiltonianSampler オブジェクト

ハミルトニアン モンテカルロ サンプラー。HamiltonianSampler オブジェクトとして指定します。

drawSamples は、smp.LogPDF 内の目標対数確率密度から標本を抽出します。サンプラーを作成するには、関数 hmcSampler を使用します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'Burnin',500,'NumSamples',2000 は、500 個のバーンイン標本を破棄してから 2000 個の標本を抽出することによりマルコフ連鎖を生成します。

Burnin — 破棄するバーンイン標本の個数

1000 (既定値) | 正の整数

マルコフ連鎖の最初から破棄するバーンイン標本の個数。正の整数を指定します。

例: 'Burnin',500

NumSamples — 抽出する標本の個数

1000 (既定値) | 正の整数

HMC サンプラーを使用してマルコフ連鎖から抽出する標本の個数。正の整数を指定します。

drawSamples メソッドは、バーンイン期間後にこの個数の標本を生成します。

例: 'NumSamples',2000

ThinSize — マルコフ連鎖の間引きサイズ

1 (既定値) | 正の整数

マルコフ連鎖の間引きサイズ。正の整数を指定します。

'ThinSize' 個の標本のうち 1 つだけが保持されます。残りの標本は破棄されます。

例: 'ThinSize',5

StartPoint — サンプリングを開始する初期点

smp.StartPoint (既定値) | 数値列ベクトル

サンプリングを開始する初期点。サンプラー smp の StartPoint プロパティと同じ要素数の数値列ベクトルを指定します。

例: 'StartPoint',randn(5,1)

VerbosityLevel — コマンド ウィンドウ出力の詳細レベル

0 (既定値) | 正の整数

サンプリング時のコマンド ウィンドウ出力の詳細レベル。0 または正の整数を指定します。

値が 0 に設定された場合、drawSamples はサンプリング時に詳細を表示しません。

値が正の整数に設定された場合、drawSamples はサンプリングの詳細を表示します。出力の頻度を設定するには、名前と値のペアの引数 'NumPrint' を使用します。

drawSamples は、次の列がある表として出力を表示します。

見出し	説明
ITER	反復回数
LOG PDF	現在の反復における対数確率密度
STEP SIZE	現在の反復におけるリープフロッグ法のステップ サイズ。ステップ サイズが微変動する場合、この値は反復間で変化する可能性があります。
NUM STEPS	現在の反復におけるリープフロッグ法のステップ数。ステップ数が微変動する場合、この値は反復間で変化する可能性があります。
ACC RATIO	採択比率、つまり採択された提案の割合。採択比率は、バーンイン期間を含めてサンプリングの最初から計算されます。
DIVERGENT	リープフロッグ反復で NaN または Inf が発生したために有効な提案をサンプラーが生成できなかった回数。標本を抽出するときに、DIVERGENT 列の非ゼロ値は、選択されたステップ サイズが状態空間のいずれかの領域で安定しきい値を上回っていることを示します。この問題を解決するには、StepSize をより小さい値に設定し、新しい標本を抽出して、DIVERGENT 列の値がすべて 0 になることを確認します。

例: 'VerbosityLevel',1

NumPrint — 詳細出力の頻度

100 (既定値) | 正の整数

詳細出力の頻度。正の整数を指定します。

'VerbosityLevel' の値が正の整数である場合、drawSamples は 'NumPrint' 回の反復ごとにサンプリングの詳細を出力します。

例: 'NumPrint',200

出力引数

chain — ハミルトニアン モンテカルロを使用して生成されたマルコフ連鎖

数値行列

ハミルトニアン モンテカルロを使用して生成されたマルコフ連鎖。数値行列として返されます。

chain の各行は標本であり、各列は 1 つのサンプリング変数を表します。

endpoint — マルコフ連鎖の最終状態

数値列ベクトル

マルコフ連鎖の最終状態。smp.StartPoint と同じ長さの数値列ベクトルとして返されます。

accratio — 採択比率

数値スカラー

マルコフ連鎖の提案の採択比率。数値スカラーとして返されます。採択比率は、バーンイン期間を含めてサンプリングの最初から計算されます。

例

HMC サンプラーの使用による標本の抽出

ハミルトニアン モンテカルロ (HMC) サンプラーを使用して多変量正規分布の MCMC 連鎖を作成します。

サンプリングするパラメーターの個数とその平均を定義します。

NumParams = 100;
means = randn(NumParams,1);
standevs = 0.1;

はじめに、多変量正規対数確率密度およびその勾配を返す関数 normalDistGrad を MATLAB® パス上に保存します (normalDistGrad はこの例の終わりで定義します)。次に、引数を指定してこの関数を呼び出し、関数 hmcSampler の入力引数 logpdf を定義します。

logpdf = @(theta)normalDistGrad(theta,means,standevs);

サンプラーの開始点を選択します。HMC サンプラーを作成し、そのパラメーターを調整します。

startpoint = randn(NumParams,1);
smp = hmcSampler(logpdf,startpoint);
smp = tuneSampler(smp);

いくつかの独立した連鎖を使用して、事後密度から標本を抽出します。各連鎖について、ランダムに分布している異なる開始点を選択します。マルコフ連鎖の先頭から破棄するバーンイン標本の数と、バーンイン後に生成する標本の数を指定します。1 番目の連鎖についてサンプリング時に詳細を出力するように 'VerbosityLevel' を設定します。

NumChains  = 4;
chains     = cell(NumChains,1);
Burnin     = 500;
NumSamples = 2000;
for c = 1:NumChains
    if c == 1
        showOutput = 1;
    else
        showOutput = 0;
    end
    chains{c} = drawSamples(smp,'Burnin',Burnin,'NumSamples',NumSamples,...
        'Start',randn(size(startpoint)),'VerbosityLevel',showOutput,'NumPrint',500);
end

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      500 |  8.450463e+01 |   4.776e-01 |           5 |   9.060e-01 |           0 |
|     1000 |  8.034444e+01 |   4.776e-01 |           9 |   8.810e-01 |           0 |
|     1500 |  9.156276e+01 |   4.776e-01 |           2 |   8.867e-01 |           0 |
|     2000 |  8.027782e+01 |   2.817e-02 |           6 |   8.890e-01 |           0 |
|     2500 |  9.892440e+01 |   4.648e-01 |           2 |   8.904e-01 |           0 |

ランダムな標本を取得した後で収束や混合などの問題を調べて、標本が対象の分布からの無作為な実現の妥当な集合を表しているかどうかを判断します。出力を確認するため、1 番目の連鎖を使用して最初のいくつかの変数について標本のトレース プロットをプロットします。

サンプリング開始点の影響を抑えるため、一定数のバーンイン標本が削除されています。さらに、トレース プロットは、目に見える長周期の相関が標本間にない高周波ノイズのように見えます。これは、連鎖が十分に混合されていることを示します。

for p = 1:3
    subplot(3,1,p);
    plot(chains{1}(:,p));
    ylabel(smp.VariableNames(p))
    axis tight
end
xlabel('Iteration')

関数 normalDistGrad は、startpoint と同じ長さの列ベクトルまたはスカラーとして指定された、Mu に格納されている平均および Sigma に格納されている標準偏差を使用して、多変量正規確率密度の対数を返します。2 番目の出力引数は、対応する勾配です。

function [lpdf,glpdf] = normalDistGrad(X,Mu,Sigma)
Z = (X - Mu)./Sigma;
lpdf = sum(-log(Sigma) - .5*log(2*pi) - .5*(Z.^2));
glpdf = -Z./Sigma;
end

ヒント

• 関数 hmcSampler を使用して HMC サンプラーを作成した後で HamiltonianSampler クラスのメソッドを使用して、MAP (最大事後確率) 点推定の計算、サンプラーの調整、標本の抽出、収束診断のチェックを行うことができます。このワークフローの例については、ハミルトニアン モンテカルロの使用によるベイズ線形回帰を参照してください。

バージョン履歴

R2017a で導入

参考

関数

• hmcSampler

クラス

• HamiltonianSampler

トピック

• ハミルトニアン モンテカルロの使用によるベイズ線形回帰