一般化線形混合効果モデルの当てはめ

この例は、GLME (一般化線形混合効果モデル) を標本データに当てはめる方法を示します。

標本データの読み込み

標本データセット mfr を読み込みます。

load mfr.mat

ある製造企業は世界で 50 の工場を操業し、各工場は完成品の生産のためにバッチプロセスを実行します。同社は各バッチの欠陥数を減少させるために新たな製造プロセスを開発しました。しかし、同社の 50 か所すべてに展開させる前に、選択した工場で新プロセスをテストし、そのプロセスが効果的であることを確実にしたいと思っています。

新しいプロセスが各バッチでの欠陥数を大幅に減少させるかどうかをテストするために、同社は実験に参加する 20 の工場を無作為に選択しました。10 工場は新プロセスを実施し、残りの 10 工場は旧プロセスを用いました。

20 の工場 (i = 1, 2, ..., 20) のそれぞれで、同社は 5 つのバッチ (j = 1, 2, ..., 5) を実行し、table mfr に以下のデータを記録しました。

新プロセスの使用を示すフラグ。バッチが新プロセスを使用している場合、newprocess = 1。バッチが旧プロセスを使用している場合、newprocess = 0。
バッチの処理時間 (時間単位) (time)。
バッチの温度。摂氏 (temp)。
バッチに使用する化学薬品の供給業者 (supplier)。supplier は A、B および C の水準をもつカテゴリカル変数であり、各水準は 3 つの供給業者のいずれかを示します。
バッチ内の欠陥数 (defects)。

またデータに含まれる time_dev と temp_dev は、摂氏 20 度で 3 時間の標準プロセスから得られる時間と温度の絶対偏差をそれぞれ表します。応答変数 defects はポアソン分布になります。このデータは、シミュレーションされたものです。

同社は、新プロセスによってバッチごとの欠陥数が大幅に削減されるかどうかを判断することを望んでいますが、時間、温度および供給業者など、工場に固有な変動が原因となって品質の差が発生する可能性も考慮します。バッチごとの欠陥数はポアソン分布を使用してモデル化できます。

$d e f e c t s_{i j} \sim P o i s s o n (μ_{i j})$

一般化線形混合効果モデルを使用し、バッチごとの欠陥数をモデル化します。

$\log (μ_{i j}) = β_{0} + β_{1} n e w p r o c e s s_{i j} + β_{2} t i m e_d e v_{i j} + β_{3} t e m p_d e v_{i j} + β_{4} s u p p l i e r_C_{i j} + β_{6} s u p p l i e r_B_{i j} + b_{i}$ ,

ここで

$d e f e c t s_{i j}$ は、バッチ "j" 処理中の工場 "i" で実行されたバッチで観測された欠陥数です。
$μ_{i j}$ は、バッチ "j" (j = 1, 2, ..., 5) 処理中の工場 "i" (i = 1, 2, ..., 20) に対応する欠陥の平均数です。
$n e w p r o c e s s_{i j}$ 、 $t i m e_d e v_{i j}$ および $t e m p_d e v_{i j}$ は、バッチ "j" 処理中の工場 "i" に対応する各変数の測定値です。たとえば $n e w p r o c e s s_{i j}$ は、工場 "i" で実行されたバッチ "j" 処理中に新プロセスが使用されたかどうかを示します。
$s u p p l i e r_C_{i j}$ および $s u p p l i e r_B_{i j}$ はエフェクト (ゼロサム) コーディングを使用するダミー変数であり、バッチ "j" 処理中に工場 "i" で実行されたバッチに対して、それぞれ会社 C または B が加工化学薬品を供給したかどうかを示します。
$b_{i} \sim N (0, σ_{b}^{2})$ は、工場特有の品質変動に相当する、各工場 "i" の変量効果の切片です。

GLME モデルの当てはめと結果の解釈

固定効果予測子として newprocess、time_dev、temp_dev および supplier を使用して一般化線形混合効果モデルを当てはめます。工場特有の変動に起因して品質に差がある可能性を考慮するために、工場別にグループ化された切片の変量効果項を含めます。応答変数 defects はポアソン分布であり、このモデルの適切なリンク関数は log です。係数の予測にラプラス近似メソッドを使用します。ダミー変数エンコードを 'effects' として指定すると、ダミー変数の係数の合計が 0 になります。

glme = fitglme(mfr,...
'defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1|factory)',...
'Distribution','Poisson','Link','log','FitMethod','Laplace',...
'DummyVarCoding','effects')

glme = 
Generalized linear mixed-effects model fit by ML

Model information:
    Number of observations             100
    Fixed effects coefficients           6
    Random effects coefficients         20
    Covariance parameters                1
    Distribution                    Poisson
    Link                            Log   
    FitMethod                       Laplace

Formula:
    defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1 | factory)

Model fit statistics:
    AIC       BIC       LogLikelihood    Deviance
    416.35    434.58    -201.17          402.35  

Fixed effects coefficients (95% CIs):
    Name                   Estimate     SE          tStat       DF    pValue        Lower        Upper    
    {'(Intercept)'}           1.4689     0.15988      9.1875    94    9.8194e-15       1.1515       1.7864
    {'newprocess' }         -0.36766     0.17755     -2.0708    94      0.041122     -0.72019    -0.015134
    {'time_dev'   }        -0.094521     0.82849    -0.11409    94       0.90941      -1.7395       1.5505
    {'temp_dev'   }         -0.28317      0.9617    -0.29444    94       0.76907      -2.1926       1.6263
    {'supplier_C' }        -0.071868    0.078024     -0.9211    94       0.35936     -0.22679     0.083051
    {'supplier_B' }         0.071072     0.07739     0.91836    94       0.36078    -0.082588      0.22473

Random effects covariance parameters:
Group: factory (20 Levels)
    Name1                  Name2                  Type           Estimate
    {'(Intercept)'}        {'(Intercept)'}        {'std'}        0.31381 

Group: Error
    Name                        Estimate
    {'sqrt(Dispersion)'}        1

Model information 表は標本データの観測値の合計 (100)、固定効果および変量効果係数の数 (それぞれ 6 および 20)、共分散パラメーターの数 (1) を表示しています。また、応答変数は Poisson 分布であり、リンク関数は Log であり、近似メソッドが Laplace であることもわかります。

Formula はウィルキンソンの表記法によるモデル仕様を示します。

Model fit statistics 表はモデルの適合度の評価に使用された統計を表します。これには赤池情報量基準 (AIC)、ベイズ情報量基準 (BIC) 値、対数尤度 (LogLikelihood) および逸脱度 (Deviance) の値が含まれます。

Fixed effects coefficients 表は、fitglme が 95% の信頼区間を返したことを示します。これには固定効果予測子ごとに 1 行が含まれ、各列にはその予測子に対応する統計が含まれます。列 1 (Name) には各固定効果係数の名前が含まれ、列 2 (Estimate) にはその推定値が含まれ、列 3 (SE) には係数の標準誤差が含まれます。列 4 (tStat) には係数が 0 に等しいという仮説検定のための "t" 統計量が含まれます。列 5 (DF) と列 6 (pValue) には "t" 統計量に対応する自由度と "p" 値がそれぞれ含まれます。最後の 2 列 (Lower および Upper) には、各固定効果係数の 95% 信頼区間の下限と上限がそれぞれ表示されます。

Random effects covariance parameters は各グループ化変数 (ここでは factory のみ) の表を表示します。これには水準の総数 (20)、共分散パラメーターのタイプおよび推定値が含まれます。ここでの std は、工場の予測子に関連付けられている変量効果の標準偏差が fitglme から返されることを示します。この推定値は 0.31381 です。また、誤差パラメーターのタイプ (ここでは分散パラメーターの平方根) およびその推定値 1 を含む表も表示します。

fitglme により生成される標準表示は変量効果パラメーターの信頼区間を指定しません。covarianceParameters を使用して、これらの値を計算し表示します。

変量効果の有意性のチェック

工場によりグループ化された変量効果切片が統計的に有意であるかどうかを判定するには、推定共分散パラメーターに対する信頼区間を計算します。

[psi,dispersion,stats] = covarianceParameters(glme);

covarianceParameters は psi の推定共分散パラメーター、推定分散パラメーター dispersion および関連する統計の cell 配列 stats を返します。stats の最初のセルは factory に関する統計を含み、2 番目のセルは分散パラメーターに関する統計を含みます。

stats の最初のセルを表示し、factory の推定共分散パラメーターに対する信頼区間を確認します。

stats{1}

ans = 
    Covariance Type: Isotropic

    Group      Name1                  Name2                  Type           Estimate    Lower      Upper  
    factory    {'(Intercept)'}        {'(Intercept)'}        {'std'}        0.31381     0.19253    0.51148

列 Lower および Upper は、factory の推定共分散パラメーターに関する既定の 95% の信頼区間を表示します。区間 [0.19253,0.51148] は 0 を含まないため、変量効果切片は 5% の有意水準において有意です。したがって、新たな製造プロセスの効果について結論を出す前に、工場に固有の変動が原因となる変量効果を考慮しなければなりません。

2 つのモデルの比較

factory によりグループ化された変量効果切片を含む混合効果モデルを、変量効果を含まないモデルと比較し、データにより適合しているのはどちらのモデルかを判定します。固定効果予測子 newprocess、time_dev、temp_dev および supplier のみを使用し、最初のモデル FEglme を当てはめます。2 番目のモデル glme を当てはめると、これらの同じ固定効果予測子を使用しますが、factory によりグループ化された変量効果切片を含めます。

FEglme = fitglme(mfr,...
'defects ~ 1 + newprocess + time_dev + temp_dev + supplier',...
'Distribution','Poisson','Link','log','FitMethod','Laplace');

glme = fitglme(mfr,...
'defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1|factory)',...
'Distribution','Poisson','Link','log','FitMethod','Laplace');

尤度比検定を使用して 2 つのモデルを比較します。'CheckNesting' を true として指定すると、compare は入れ子要件が満たされていない場合に警告を返します。

results = compare(FEglme,glme,'CheckNesting',true)

results = 
    Theoretical Likelihood Ratio Test

    Model     DF    AIC       BIC       LogLik     LRStat    deltaDF    pValue    
    FEglme    6     431.02    446.65    -209.51                                   
    glme      7     416.35    434.58    -201.17    16.672    1          4.4435e-05

compare は各モデルの自由度 (DF)、赤池情報量基準 (AIC)、ベイズ情報量基準 (BIC) および対数尤度値を返します。glme は FEglme よりも AIC、BIC および対数尤度値が小さくなっているため、glme (工場によりグループ化された切片に対する変量効果項を含むモデル) はこのデータに関してはより当てはまるモデルであることを示しています。加えて、"p" 値が小さい場合、compare は応答ベクトルが混合効果モデル glme により生成されたという対立仮説を優先して、応答ベクトルが固定効果専用モデル FEglme により生成されたという帰無仮説を棄却することを示します。

結果のプロット

モデルの当てはめた条件付き平均値を生成します。

mufit = fitted(glme);

観測された応答値と近似応答値をプロットします。

figure
scatter(mfr.defects,mufit)
title('Observed Values versus Fitted Values')
xlabel('Fitted Values')
ylabel('Observed Values')

Figure contains an axes object. The axes object with title Observed Values versus Fitted Values, xlabel Fitted Values, ylabel Observed Values contains an object of type scatter.

条件付きピアソン残差を使用して診断プロットを作成し、モデルの仮定を検定します。一般化線形混合効果モデルの生の残差には観測間で定数分散がないため、条件付きピアソン残差を代わりに使用します。

ピアソン残差の平均が 0 に等しいことを視覚的に確認するため、ヒストグラムをプロットします。モデルが正しい場合、ピアソン残差の中心は 0 になっているはずです。

plotResiduals(glme,'histogram','ResidualType','Pearson')

Figure contains an axes object. The axes object with title Histogram of residuals, xlabel Residuals, ylabel Probability density contains an object of type patch.

ヒストグラムは、ピアソン残差が 0 を中心にしていることを示します。

ピアソン残差と当てはめた値をプロットして残差間の非定数分散の兆候 (不均一分散) を確認します。条件付きピアソン残差には、一定の分散があると予測されます。したがって、条件付きピアソン残差と条件付きの当てはめた値のプロットは、条件付き近似値において体系的な依存性を示さないはずです。

plotResiduals(glme,'fitted','ResidualType','Pearson')

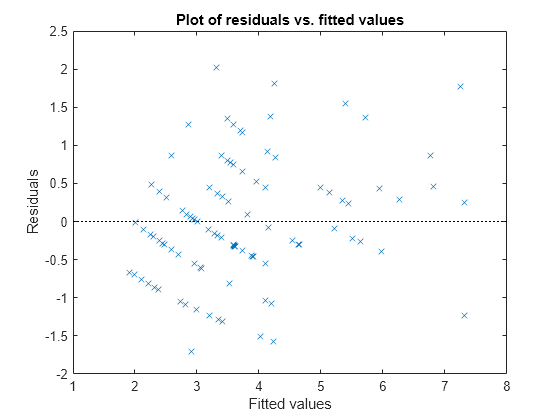
Figure contains an axes object. The axes object with title Plot of residuals vs. fitted values, xlabel Fitted values, ylabel Residuals contains 2 objects of type line. One or more of the lines displays its values using only markers

このプロットは当てはめた値において体系的な依存性を示さず、残差間でも非定数分散の兆候がありません。

ピアソン残差とラグ付き残差をプロットして、残差間の相関を確認します。GLME の条件付き独立仮定は、条件付きピアソン残差がほぼ無相関であることを示します。

plotResiduals(glme,'lagged','ResidualType','Pearson')

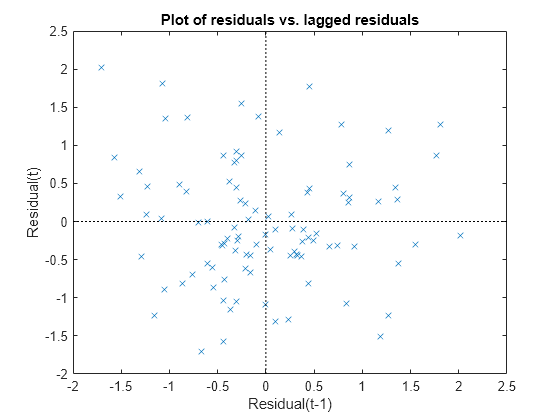
Figure contains an axes object. The axes object with title Plot of residuals vs. lagged residuals, xlabel Residual(t-1), ylabel Residual(t) contains 3 objects of type line. One or more of the lines displays its values using only markers

プロットにパターンはありません。そのため、残差間で相関の兆候はありません。

参考

fitglme | GeneralizedLinearMixedModel

トピック

一般化線形モデル