生存データまたは信頼性データの分析

寿命データの特徴

寿命データには、他のタイプのデータにはない、顕著な特徴があります。第 1 に、寿命データの値は常に正であり、通常は時間を表します。第 2 に、寿命データの中には、正確に観測されず、一部の値よりも大きいことのみがわかるようなデータがあります。第 3 の特徴は、よく使用される分布と分析方法が寿命データに特化したものであるということです。

100 個のスロットルを故障するまでテストした結果のシミュレーションを実行してみましょう。ほとんどのスロットルは寿命がかなり長く、少数のスロットルは非常に早く故障する傾向があった場合に観測されるデータを生成します。

rng(2,'twister');
lifetime = [wblrnd(15000,3,90,1); wblrnd(1500,3,10,1)];

この例では、現場で実際に 100 時間使用した状況を各テスト時間で再現できるように、厳しい条件下でスロットルをテストすると仮定します。多くの場合、実践的な理由のため、信頼性試験は一定の時間が経過すると停止されます。この例では、140 時間を採用します。これは、実際の稼働時間が 14,000 時間に達した状況に相当します。試験中に故障するものもあれば、140 時間故障しないものもあります。実際の試験では、後者の時間は 14,000 として記録されます。これを、シミュレートされたデータで再現します。また、故障時間を並べ替えることもよく行われます。

T = 14000;
obstime = sort(min(T, lifetime));

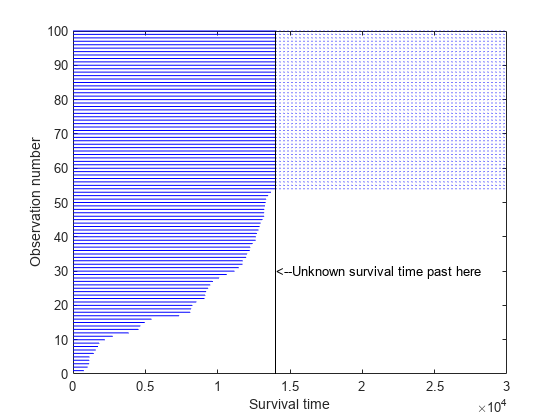
試験で故障しなかったスロットルもいずれは故障することは理解できますが、実際の故障時間を観測できるほど試験期間は長くありません。この試験から判断できるのは、それらのスロットルの寿命が 14,000 時間以上であることのみです。このような値を、打ち切られた値と呼びます。次のプロットは、データの約 40% が 14,000 で打ち切られていることを示しています。

failed = obstime(obstime<T); nfailed = length(failed);
survived = obstime(obstime==T); nsurvived = length(survived);
censored = (obstime >= T);
plot([zeros(size(obstime)),obstime]', repmat(1:length(obstime),2,1), ...
     'Color','b','LineStyle','-')
line([T;3e4], repmat(nfailed+(1:nsurvived), 2, 1), 'Color','b','LineStyle',':');
line([T;T], [0;nfailed+nsurvived],'Color','k','LineStyle','-')
text(T,30,'<--Unknown survival time past here')
xlabel('Survival time'); ylabel('Observation number')

分布を調べる方法

データの分布を観測する前に、確率分布を調べるさまざまな方法を検討してみましょう。

ワイブル分布を使用した、これら 4 つのプロット タイプの例を以下に示しています。ワイブル分布は、寿命データのモデル化によく使用されています。

x = linspace(1,30000);
subplot(2,2,1);
plot(x,wblpdf(x,14000,2),x,wblpdf(x,18000,2),x,wblpdf(x,14000,1.1))
title('Prob. Density Fcn')
subplot(2,2,2);
plot(x,1-wblcdf(x,14000,2),x,1-wblcdf(x,18000,2),x,1-wblcdf(x,14000,1.1))
title('Survivor Fcn')
subplot(2,2,3);
wblhaz = @(x,a,b) (wblpdf(x,a,b) ./ (1-wblcdf(x,a,b)));
plot(x,wblhaz(x,14000,2),x,wblhaz(x,18000,2),x,wblhaz(x,14000,1.1))
title('Hazard Rate Fcn')
subplot(2,2,4);
probplot('weibull',wblrnd(14000,2,40,1))
title('Probability Plot')

ワイブル分布の近似

ワイブル分布は、指数分布を一般化したものです。寿命が指数分布に従う場合、寿命のハザード率は一定です。これは、寿命が経年変化しないことを意味します。つまり、ある区間において故障が観測される確率は、その区間の開始までの生存が与えられていれば、区間がどこで始まろうが関係ない、ということを意味します。ワイブル分布では、ハザード率が増減することがあります。

寿命データのモデル化に使用される他の分布として、対数正規分布、ガンマ分布、およびバーンバウム・サンダース分布が挙げられます。

可能な各生存時間までに故障する比率を示す、データの経験累積分布関数をプロットします。点線の曲線によって、これらの確率の 95% 信頼区間が与えられます。

subplot(1,1,1);
[empF,x,empFlo,empFup] = ecdf(obstime,'censoring',censored);
stairs(x,empF);
hold on;
stairs(x,empFlo,':'); stairs(x,empFup,':');
hold off
xlabel('Time'); ylabel('Proportion failed'); title('Empirical CDF')

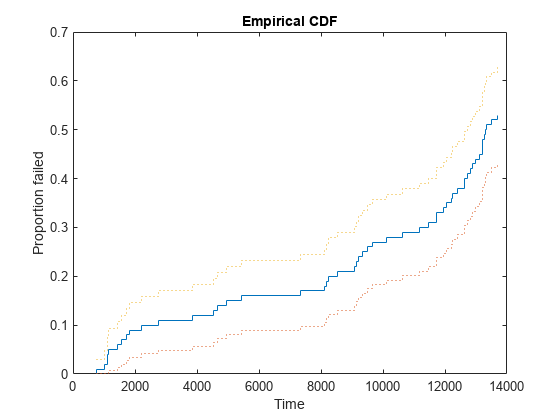
このプロットからわかるように、たとえば、4,000 時間までに故障する比率は約 12% であり、この時間までの故障確率の 95% 信頼限界は 6% ～ 18% です。試験は 14,000 時間しか実施されていないため、経験累積分布関数を使用して計算できるのは、その限度までの故障確率にすぎません。データの約半分が 14,000 で打ち切られているため、経験累積分布関数は、1.0 ではなく約 0.53 まで上がるだけです。

ワイブル分布は通常、装置故障に適したモデルです。関数 wblfit は、ワイブル分布をデータ (打ち切りを伴うデータを含む) に当てはめます。パラメーター推定を計算した後、それらの推定を使用して近似ワイブル分布の累積分布関数を評価します。累積分布関数の値は推定されたパラメーターに基づくため、それらの信頼限界を計算します。

paramEsts = wblfit(obstime,'censoring',censored);
[nlogl,paramCov] = wbllike(paramEsts,obstime,censored);
xx = linspace(1,2*T,500);
[wblF,wblFlo,wblFup] = wblcdf(xx,paramEsts(1),paramEsts(2),paramCov);

経験累積分布関数と近似累積分布関数のプロットを重ね合わせることができます。こうすることで、スロットルの信頼性データがワイブル分布によって、どの程度適切にモデル化されるかを判断できます。

stairs(x,empF);
hold on
handles = plot(xx,wblF,'r-',xx,wblFlo,'r:',xx,wblFup,'r:');
hold off
xlabel('Time'); ylabel('Fitted failure probability'); title('Weibull Model vs. Empirical')

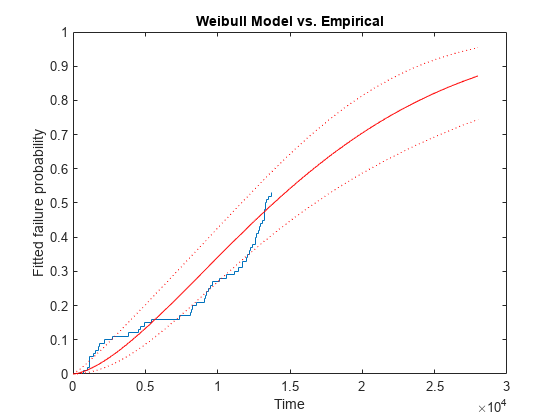
ワイブル モデルを使用すると、試験が終了した後の時間における故障確率を予想し、計算することができます。しかし、近似曲線がデータと十分に一致しないように思われます。2,000 時間より前の初期故障が、ワイブル モデルで予想されるよりもはるかに多く、その結果、約 7,000 ～ 約 13,000 時間における初期故障が非常に少なくなっています。これは驚くことではありません。この種の動作を伴うデータを生成したことを思い出してください。

滑らかなノンパラメトリック推定の追加

Statistics and Machine Learning Toolbox™ に用意されている事前定義済み関数には、このような過剰な初期故障がある分布は含まれていません。その代わり、関数 ksdensity を使用して、経験累積分布関数を介した滑らかなノンパラメトリック曲線を描画することができます。ワイブル累積分布関数の信頼帯を取り除き、2 つの曲線を追加します。一方の曲線は既定の平滑化パラメーターを使用したもので、他方の曲線は既定値の 1/3 の平滑化パラメーターを使用したものです。平滑化パラメーターが小さいほど、曲線がより密接にデータに追従します。

delete(handles(2:end))
[npF,ignore,u] = ksdensity(obstime,xx,'cens',censored,'function','cdf');
line(xx,npF,'Color','g');
npF3 = ksdensity(obstime,xx,'cens',censored,'function','cdf','width',u/3);
line(xx,npF3,'Color','m');
xlim([0 1.3*T])
title('Weibull and Nonparametric Models vs. Empirical')
legend('Empirical','Fitted Weibull','Nonparametric, default','Nonparametric, 1/3 default', ...
       'location','northwest');

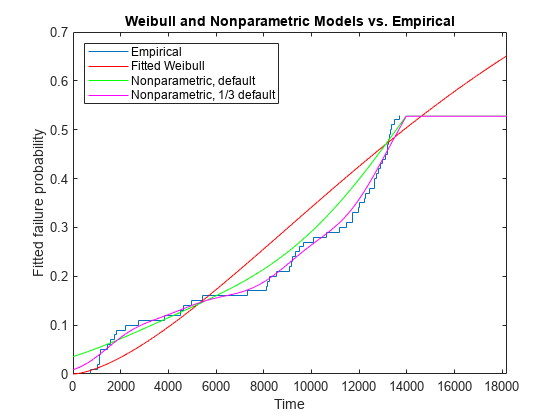
より小さい平滑化パラメーターを使用したノンパラメトリック推定は、十分にデータと一致します。しかし、経験累分布関数と同様に、テストが終了した後にノンパラメトリック モデルを外挿することは不可能です。つまり、推定された累積分布関数が、最後の観測の後は平坦になります。

このノンパラメトリック近似のハザード率を計算し、データの範囲全体にわたってプロットしてみましょう。

hazrate = ksdensity(obstime,xx,'cens',censored,'width',u/3) ./ (1-npF3);
plot(xx,hazrate)
title('Hazard Rate for Nonparametric Model')
xlim([0 T])

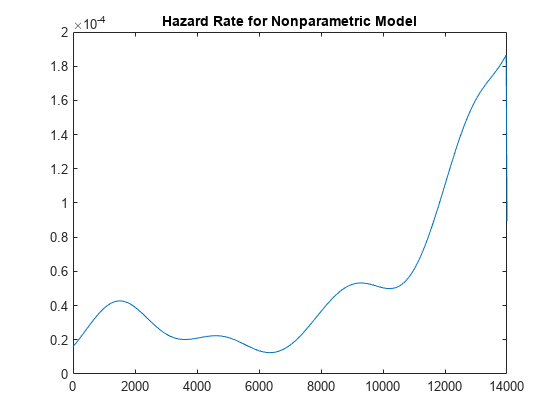
この曲線は "バスタブ" のような形状をしており、ハザード率が 2,000 付近で高く、その後、低い値になり、次に再び上昇しています。これは、寿命の早期に故障しやすく (初期故障)、寿命の後期に再び故障しやすい (経年劣化) コンポーネントに典型的なハザード率です。

また、ノンパラメトリック モデルにおける打ち切られていない最大の観測を超えてハザード率を推定することはできず、グラフがゼロまで下がることに注意してください。

代替モデル

この例で使用した、シミュレートされたデータの場合、ワイブル分布は適切な近似ではないことがわかりました。ノンパラメトリック近似を使用すると、十分にデータを当てはめることができましたが、そのモデルは、そのデータの範囲内でのみ役に立ちました。

代替法は、異なるパラメトリック分布を使用するというものです。Statistics and Machine Learning Toolbox には、対数正規分布、ガンマ分布、バーンバウム・サンダース分布など他の一般的な寿命分布向けの関数と、寿命モデルではあまり使用されない他の分布向けの関数が含まれています。また、カスタム分布当てはめ時の数値問題の回避の例で説明されているように、カスタム パラメトリック モデルを定義して、寿命データに当てはめることもできます。

さらに別の方法は、2 つのパラメトリック分布 (一方は初期故障を表し、他方は残りの分布を表す) を組み合わせて使用するというものです。分布の混合の当てはめについては、カスタム分布の当てはめの例で説明します。