SM ST10C
Discrete-time or continuous-time synchronous machine ST10C static excitation system with automatic voltage regulator
Since R2023a
Libraries:
Simscape /
Electrical /
Control /
SM Control
Description
The SM ST10C block implements a synchronous-machine-type ST10C static excitation system model in conformance with IEEE Std 421.5-2016 [1].
Use this block to model the control and regulation of the field voltage of a synchronous machine.
Switch between continuous and discrete implementations of the block by using the
Sample time (-1 for inherited) parameter. To configure the
integrator for continuous time, set the Sample time (-1 for
inherited) parameter to 0. To configure the integrator
for discrete time, set the Sample time (-1 for inherited) parameter
to a positive scalar. To inherit the sample time from an upstream block, set the
Sample time (-1 for inherited) parameter to
-1.
The SM ST10C block comprises four major components:
The Current Compensator component modifies the measured terminal voltage as a function of the terminal current.
The Voltage Measurement Transducer component simulates the dynamics of a terminal voltage transducer using a low-pass filter.
The Excitation Control Elements component compares the voltage transducer output with a terminal voltage reference to produce a voltage error value. The component then passes this value through a voltage regulator to produce the field voltage.
The Power Source component models the power source for the controlled rectifier when it is independent from the terminal voltage.
This diagram shows the structure of the ST10C excitation system model:
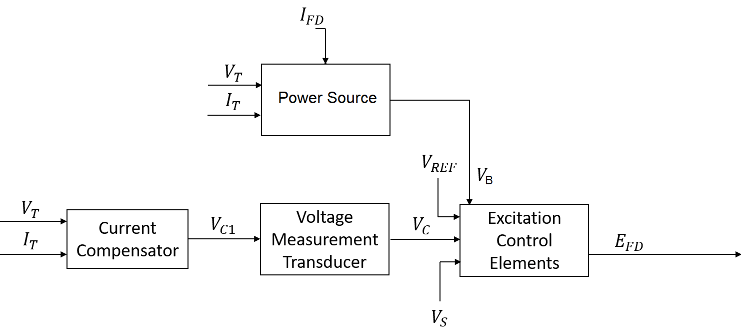
In the diagram:
VT and IT are the measured terminal voltage and current of the synchronous machine, respectively.
VC1 is the current-compensated terminal voltage.
VC is the filtered, current-compensated terminal voltage.
VREF is the reference terminal voltage.
VS is the power system stabilizer voltage.
VB is the exciter field voltage.
EFD and IFD are the field voltage and current, respectively.
Current Compensator and Voltage Measurement Transducer
The block models the current compensator by using this equation:
where:
RC is the load compensation resistance.
XC is the load compensation reactance.
The block implements the voltage measurement transducer as a Low-Pass Filter block with the time constant TR. Refer to the documentation for the Low-Pass Filter block for information about the exact discrete and continuous implementations.
Excitation Control Elements
This diagram shows the structure of the excitation control elements:

In the diagram:
The Summation Point Logic subsystem models the summation point input location for the overexcitation limiter (OEL), underexcitation limiter (UEL), and stator current limiter (SCL). For more information about using limiters with this block, see Field Current Limiters.
There are two Take-over Logic subsystems. They model the take-over point input location for the OEL, UEL and SCL voltages. For more information about using limiters with this block, see Field Current Limiters.
A parallel configuration of Lead-Lag (Discrete or Continuous) blocks offer independent control settings when a limiter is active. The model offers a common gain factor KR and two Lead-Lag (Discrete or Continuous) blocks for the AVR and for the underexcitation and overexcitation limiters. The SW_UEL and SW_OEL Switch blocks activate the appropriate control path when the VUEL and/or VOEL signals are connected to their respective alternate positions. The SW_UEL and SW_OEL Switch blocks are on position B when you set the Alternate UEL input locations (V_UEL) and Alternate OEL input locations (V_OEL) parameters to
Take-over at voltage error.The two Lead-Lag blocks in each control path model additional dynamics associated with the voltage regulator and with the underexcitation and overexcitation limiters. The first Lead-Lag block in each respective path represents a transient gain reduction, where TC2 (or TUC2 and TOC2) is the lead time constant and TB2 (or TUB2 and TOB2) is the lag time constant. The second Lead-Lag block allows the possibility of representing a transient gain increase, where TC1 (or TUC1 and TOC1) is the lead time constant and TB1 (or TUB1 and TOB1) is the lag time constant. See the documentation for the Lead-Lag block for information about the discrete and continuous implementations.
The SM ST10C block also offers the option to apply the PSS signal at the AVR summing junction after the first Take-over Logic subsystem or at the output of the gate structure, through a separate path (the bottom path in the model). This separate path comprises the same control elements as the main summing junction path.
The Power source selector parameter controls the origin of the power source for the controlled rectifier. The subsystem multiplies the voltage regulator command signal VRby the exciter field voltage VB. For more information about the logical switch for the power source of the controlled rectifier, see Power Source.
Field Current Limiters
You can use different types of field current limiter to modify the output of the voltage regulator under unsafe operating conditions:
Use an overexcitation limiter to prevent overheating of the field winding due to excessive field current demand.
Use an underexcitation limiter to boost field excitation when it is too low, which risks desynchronization.
Use a stator current limiter to prevent overheating of the stator windings due to excessive current.
Attach the output of any of these limiters at one of these points:
Summation point — Use the limiter as part of the automatic voltage regulator (AVR) feedback loop.
Take-over points — Override the usual behavior of the AVR.
If you are using the stator current limiter at the summation point, use the input VSCLsum. If you are using the stator current limiter at the take-over point, use the overexcitation input VSCLoel, and the underexcitation input VSCLuel.
Power Source
You can use different power source representations for the controlled rectifier by
setting the Power source selector parameter value. To derive
the power source for the controlled rectifier from the terminal voltage, set the
Power source selector parameter to Position A:
power source derived from generator terminal voltage. To specify
that the power source is independent of the terminal voltage, set the
Power source selector parameter to Position B:
power source independent of generator terminal conditions.
This diagram shows a model of the exciter power source utilizing a phasor combination of the terminal voltage VT and terminal current IT:

Ports
Input
Output
Parameters
References
[1] IEEE Std 421.5-2016 (Revision of IEEE Std 421.5-2005). "IEEE Recommended Practice for Excitation System Models for Power System Stability Studies." Piscataway, NJ: IEEE, 2016.
Extended Capabilities
Version History
Introduced in R2023a
