このページは前リリースの情報です。該当の英語のページはこのリリースで削除されています。

Battery

汎用バッテリー モデル

• 

ライブラリ:
Simscape / Electrical / Specialized Power Systems / Sources

説明

Battery ブロックは、最も一般的なタイプの充電式バッテリーを表す汎用の動的モデルを実装します。

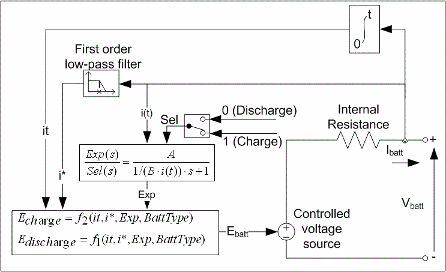
次の図は、ブロックでモデル化される等価回路を示しています。

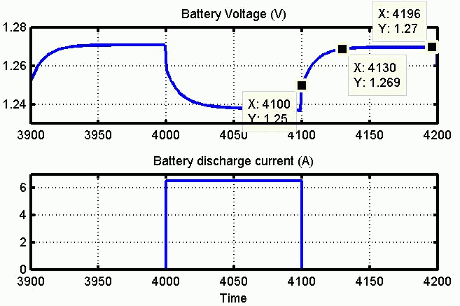
充電特性と放電特性

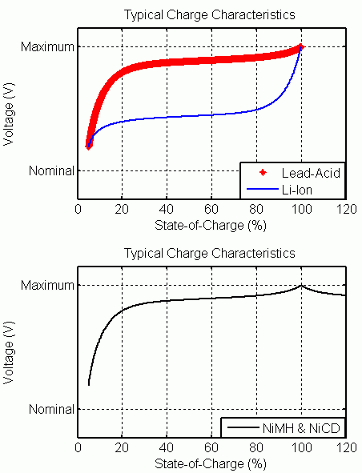
回路のパラメーターを変更して、特定のバッテリー タイプとその放電特性を表すことができます。一般的な放電曲線は 3 つのセクションで構成されます。

最初のセクションは、バッテリー充電時の指数電圧降下を表します。降下の幅はバッテリー タイプによって異なります。2 番目のセクションは、電圧降下がバッテリーのノミナル電圧を下回るまでにバッテリーから引き出すことができる電荷を表します。最後の 3 番目のセクションは、バッテリーの全放電 (電圧が急速に降下する状態) を表します。

バッテリー電流が負のときは、充電特性に従ってバッテリーが再充電されます。

モデルのパラメーターは放電特性から導出されます。放電と充電の特性は同じであると仮定されます。

Exp(s) 伝達関数は、鉛蓄電池、ニッケルカドミウム (NiCD) 電池、およびニッケル水素 (NiMH) 電池の充電サイクルと放電サイクルにおけるヒステリシス現象を表します。バッテリーの充電状態に関係なく、バッテリーの充電中は指数電圧が上昇します。バッテリーの放電中は指数電圧が即座に降下します。

バッテリーの充電状態 (SOC) は、バッテリーの電荷を満充電に対する割合として表した尺度です。放電深度 (DOD) は SOC の補数で、DOD = 100% - SOC となります。

たとえば、SOC に応じて次のようになります。

• 100% — バッテリーが完全に充電されていて、DOD は 0% です。

• 75% — バッテリーが 3/4 まで充電されていて、DOD は 25% です。

• 50% — バッテリーが 1/2 まで充電されていて、DOD は 50% です。

• 0% — バッテリーの電荷が 0 で、DOD は 100% です。

モデルの検証

モデルの実験的検証では、充電 (電流が 0 ～ 2 C のとき) と放電 (電流が 0 ～ 5 C のとき) のダイナミクスの最大誤差は 5% (SOC が 10% ～ 100% のとき) となっています。

パラメーター化

データ シートからのバッテリー パラメーターの抽出

次の図は、Panasonic NiMH-HHR650D バッテリーのデータ シートから抽出した詳細なパラメーターを示したものです。

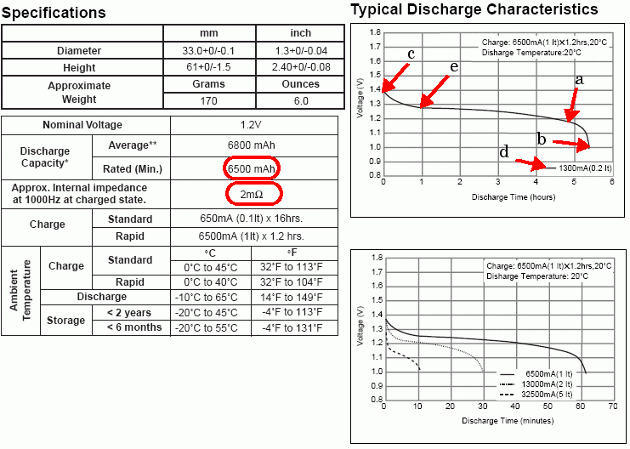
定格容量と内部抵抗は仕様の表から得られます。それ以外の詳細なパラメーターは「Typical Discharge Characteristics」のプロットから導出されます。

パラメーター	値
定格容量	6.5 Ah
内部抵抗	2 mΩ
ノミナル電圧 (a)	1.18 V
定格容量	6.5 Ah
最大容量 (b)	7 Ah (5.38 h * 1.3 A)
満充電電圧 (c)	1.39 V
ノミナル放電電流 (d)	1.3 A
ノミナル電圧での容量 (a)	6.25 Ah
指数電圧 (e)	1.28 V
指数容量 (e)	1.3 Ah

これらのパラメーターは概算であり、放電曲線から得られる点の精度に左右されます。

これらのパラメーターから得られる放電曲線 (次の図の点線で示した曲線) は、データ シートの曲線に近くなっています。

直接/並列のセルのモデル化

直接/並列のセルの組み合わせを単一のセルのパラメーターに基づいてモデル化するには、次の表に示すパラメーター変換を使用します。Nb_ser 変数は直列のセルの数に対応し、Nb_par は並列のセルの数に対応します。

パラメーター	値
ノミナル電圧	1.18 * Nb_ser
定格容量	6.5 * Nb_par
最大容量	7 * Nb_par
満充電電圧	1.39 * Nb_ser
ノミナル放電電流	1.3 * Nb_par
内部抵抗	0.002 * Nb_ser/Nb_par
ノミナル電圧での容量	6.25 * Nb_par
指数領域	1.28 * Nb_ser、1.3 * Nb_par

方程式

鉛蓄電池のタイプには、次の方程式がモデルで使用されます。

• 放電モデル (i* > 0)

  $$f_1\left(it,i*,i,Exp\right)=E_0-K\cdot \frac{Q}{Q-it}\cdot i*-K\cdot \frac{Q}{Q-it}\cdot it+{\text{Laplace}}^{-1}\left(\frac{Exp(s)}{Sel(s)}\cdot 0\right)$$

• 充電モデル (i* < 0)

  $$f_2\left(it,i*,i,Exp\right)=E_0-K\cdot \frac{Q}{it+0.1\cdot Q}\cdot i*-K\cdot \frac{Q}{Q-it}\cdot it+{\text{Laplace}}^{-1}\left(\frac{Exp(s)}{Sel(s)}\cdot \frac{1}{s}\right)$$

  充電中は it > 0 です。

リチウムイオン電池のタイプには、次の方程式がモデルで使用されます。

• 放電モデル (i* > 0)

  $$f_1\left(it,i*,i\right)=E_0-K\cdot \frac{Q}{Q-it}\cdot i*-K\cdot \frac{Q}{Q-it}\cdot it+A\cdot \exp \left(-B\cdot it\right)$$

• 充電モデル (i* < 0)

  $$f_2\left(it,i*,i\right)=E_0-K\cdot \frac{Q}{it+0.1\cdot Q}\cdot i*-K\cdot \frac{Q}{Q-it}\cdot it+A\cdot \exp \left(-B\cdot it\right)$$

ニッケルカドミウム電池とニッケル水素電池のタイプには、次の方程式がモデルで使用されます。

• 放電モデル (i* > 0)

  $$f_1\left(it,i*,i,Exp\right)=E_0-K\cdot \frac{Q}{Q-it}\cdot i*-K\cdot \frac{Q}{Q-it}\cdot it+{\text{Laplace}}^{-1}\left(\frac{Exp(s)}{Sel(s)}\cdot 0\right)$$

• 充電モデル (i* < 0)

  $$f_2\left(it,i*,i,Exp\right)=E_0-K\cdot \frac{Q}{\left|it\right|+0.1\cdot Q}\cdot i*-K\cdot \frac{Q}{Q-it}\cdot it+{\text{Laplace}}^{-1}\left(\frac{Exp(s)}{Sel(s)}\cdot \frac{1}{s}\right).$$

  方程式では、次のようになります。

  • E_Batt は非線形電圧 (V) です。

  • E₀ は定電圧 (V) です。

  • Exp(s) は指数領域のダイナミクス (V) です。

  • Sel(s) はバッテリーのモードを表します。バッテリー放電中は Sel(s) = 0、バッテリー充電中は Sel(s) = 1 です。

  • K は分極定数 (V/Ah) または分極抵抗 (オーム) です。

  • i* は低周波電流のダイナミクス (A) です。

  • i はバッテリー電流 (A) です。

  • it は引き出される容量 (Ah) です。

  • Q は最大バッテリー容量 (Ah) です。

  • A は指数電圧 (V) です。

  • B は指数容量 (Ah⁻¹) です。

制限と仮定

制限

• 最小無負荷バッテリー電圧は 0 V、最大バッテリー電圧は 2 × E₀ に相当します。

• バッテリーの最小容量は 0 Ah、最大容量は Q_max です。

仮定

• 内部抵抗は充電サイクルと放電サイクルにおいて一定であると仮定され、電流の振幅によって変動しません。

• モデルのパラメーターは放電特性から導出されます。放電と充電の特性は同じであると仮定されます。

• バッテリーの容量は電流の振幅によって変動しません (ポイケルト効果はありません)。

• バッテリーの自己放電は表されません。これは、バッテリー端子と並列に大きな抵抗を追加することで表すことができます。

• バッテリーにメモリの影響はありません。

端子

出力

m — バッテリーの温度、充電状態、電流、および電圧

Simulink^® 信号 | ベクトル

バッテリーの温度、充電状態、電流、および電圧の信号の出力ベクトル。信号を逆多重化するには、Bus Selector ブロックを使用できます。

信号	定義	単位
セル温度	セル温度または内部温度	℃
SOC	バッテリーの SOC。割合 (0 ～ 100%) として表されます。満充電のバッテリーは SOC 100%、空のバッテリーは 0% です。SOC は次のように計算されます。 $$SOC=100\left(1-\frac{1}{Q}{\displaystyle {\int }_0^{t}i(t)dt}\right).$$	%
電流	バッテリー電流	A
電圧	バッテリー電圧	V

保存

+ — 正の端子

特定用途向けの電気

バッテリーの正の端子に関連付けられた特定用途向けの電気量保存端子。

- — 負の端子

特定用途向けの電気

バッテリーの負の端子に関連付けられた特定用途向けの電気量保存端子。

パラメーター

Parameters

Type — バッテリー モデル

Lithium-Ion (既定値) | Lead-Acid | Nickel-Cadmium | Nickel-Metal-Hydride

バッテリー モデル。電荷挙動があらかじめ決められた 4 つのバッテリー タイプがブロックで提供されます。

Nominal voltage (V) — ノミナル電圧

7.2 (既定値) | 正のスカラー

バッテリーのノミナル電圧 V_nom (V)。ノミナル電圧は、放電特性の線形領域の終端を表します。

Rated capacity (Ah) — 定格容量

5.4 (既定値) | 正のスカラー

バッテリーの定格容量 Q_rated (Ah)。定格容量は、バッテリーの最小有効容量です。

Initial state-of-charge (%) — 初期 SOC

100 (既定値)

シミュレーション開始時のバッテリーの充電状態 (SOC)。最大電荷量に対する割合として表されます。SOC 100% は満充電のバッテリーを示し、0% は空のバッテリーを示します。

この指定値は、[Discharge] 設定で [Plot] をクリックするとブロックによって生成される放電曲線には影響しません。

Battery response time (s) — 応答時間

30 (既定値) | 非負のスカラー

最終値の 95% でのバッテリーの応答時間 (秒)。この値は電圧のダイナミクスを表し、電流ステップが適用されるときに観察できます。

以下のプロットは、応答時間が 30 秒のバッテリーの電圧と放電電流を示しています。

Discharge

Determined from the nominal parameters of the battery — 放電パラメーターの決定

オン (既定値) | オフ

選択すると、[Parameters] 設定のパラメーターに指定した値に基づいて、ブロックで [Discharge] 設定のパラメーターが決定されます。

依存関係

このパラメーターをオンにすると、[Discharge] 設定のパラメーターは無効になります。

Maximum capacity (Ah) — 最大アンペア時容量

5.4 (既定値) | 正のスカラー

バッテリー電圧に不連続が生じるときの理論上の最大容量 Q (Ah)。一般に、この値は定格容量の 105% に相当します。

Cut-off Voltage (V) — カットオフ電圧

5.4 (既定値) | 正のスカラー

最小許容バッテリー電圧 (V)。この電圧は、放電特性の終端を表します。カットオフ電圧でバッテリーは完全に放電されます。

Fully charged voltage (V) — 満充電電圧

8.3807 (既定値) | 正のスカラー

与えられた放電電流に対する満充電電圧 V_full。満充電電圧は無負荷電圧ではありません。

Nominal discharge current (A) — ノミナル放電電流

2.3478 (既定値) | 正のスカラー

放電曲線を測定する対象のノミナル放電電流 (A)。

たとえば、1.5 Ah の NiMH 電池の一般的な放電電流は定格容量の 20% です。(0.2 * 1.5 Ah / 1 h = 0.3 A)。

Internal resistance (Ohms) — 内部抵抗

0.013333 (既定値) | 正のスカラー

バッテリーの内部抵抗 (オーム)。プリセット モデルを使用する場合、ノミナル電力 (ノミナル電圧にバッテリー定格容量を乗算) の 1% に対応する汎用値が読み込まれます。抵抗は充電サイクルと放電サイクルにおいて一定であり、電流の振幅によって変動しません。

Capacity (Ah) at nominal voltage — ノミナル電圧でのアンペア時容量

4.8835 (既定値) | 正のスカラー

電圧降下がノミナル電圧を下回るまでのバッテリーから引き出される容量 Q_nom。この値は Q_exp ～ Q_max でなければなりません。

Exponential zone [Voltage (V), Capacity (Ah)] — 指数領域の電圧と容量

[7.7788 0.2653] (既定値) | 非負のベクトル

指数領域の終端に対応する電圧 V_exp と容量 Q_exp。電圧は V_nom ～ V_full でなければなりません。容量は 0 ～ Qnom でなければなりません。

参照

[1] Omar N., M. A. Monem, Y. Firouz, J. Salminen, J. Smekens, O. Hegazy, H. Gaulous, G. Mulder, P. Van den Bossche, T. Coosemans, and J. Van Mierlo. “Lithium iron phosphate based battery — Assessment of the aging parameters and development of cycle life model.” Applied Energy, Vol. 113, January 2014, pp. 1575–1585.

[2] Saw, L.H., K. Somasundaram, Y. Ye, and A.A.O. Tay, “Electro-thermal analysis of Lithium Iron Phosphate battery for electric vehicles.” Journal of Power Sources. Vol. 249, pp. 231–238.

[3] Tremblay, O., L.A. Dessaint, "Experimental Validation of a Battery Dynamic Model for EV Applications." World Electric Vehicle Journal. Vol. 3, May 13–16, 2009.

[4] Zhu, C., X. Li, L. Song, and L. Xiang, “Development of a theoretically based thermal model for lithium ion battery pack.” Journal of Power Sources. Vol. 223, pp. 155–164.

拡張機能

C/C++ コード生成
Simulink® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2008a で導入

R2024b: 温度と経年劣化の影響を削除

Battery ブロックで温度と経年劣化の影響はモデル化されなくなりました。バッテリーの温度と経年劣化の影響をモデル化する必要がある場合は、Simscape Electrical の Battery ブロックと Battery (Table-Based) ブロックを使用します。

この変更の結果として、次の端子と以下のパラメーターは削除されました。

端子

• Ta

パラメーター

• Simulate temperature effects

• Use a preset battery

• Simulating aging effects

• Discharge current [i1, i2, i3,...] (A)

• Units

• Plot

• Initial cell temperature (deg, C)

• Nominal ambient temperature T1 (deg, C)

• Second ambient temperature T2 (deg, C)

• Maximum capacity (Ah)

• Initial discharge voltage (V)

• Voltage at 90% maximum capacity (V)

• Exponential zone [Voltage (V), Capacity (Ah)]

• Thermal resistance, cell-to-ambient (deg, C/W)

• Thermal time constant, cell-to-ambient (s)

• Heat loss difference [charge vs. discharge] (W)]

• Initial battery age (Equivalent full cycles)

• Aging model sampling time (s)

• Ambient temperature Ta1 (deg, C)

• Capacity at EOL (End Of Life) (Ah)

• Internal resistance at EOL (Ohms)

• Charge current (nominal, maximum) [Ic (A), Icmax (A)]

• Discharge current (nominal, maximum) [Id (A), Idmax (A)]

• Cycle life at 100% DOD, Ic and Id (Cycles)

• Cycle life at 25% DOD, Ic and Id (Cycles)

• Cycle life at 100% DOD, Ic and Idmax (Cycles)

• Cycle life at 100% DOD, Icmax and Id (Cycles)

• Ambient temperature Ta2 (deg, C)

参考

AC Voltage Source | DC Voltage Source