押し出しおよび回転のモデル化
押し出しおよび回転
カスタムの断面をもつ固体では、Extruded Solid ブロックと Revolved Solid ブロックを使って、Brick Solid、Cylindrical Solid、Spherical Solid などの単純な形状では通常不可能な、より正確な固体表現を作成することができます。これらは、任意でありながら、軸に沿った、または軸を中心とした一定の断面をもつ固体をモデル化する場合に使用します。Extruded Solid ブロックは [General] 押し出しまたは [Regular] 押し出しのいずれかです。
Extruded Solid ブロックとは
一般押し出しは、カスタムの断面平面に対し垂直な軸に沿った、その断面の線形スイープです。スイープは、Extruded Solid ブロックのダイアログ ボックスで指定された長さにわたって行われます。穴がある場合には断面の指定規則は若干異なりますが、断面は任意の輪郭と 1 つ以上の中空セクションをもつことができます。
一般押し出しの例には、まっすぐなビーム、プレート、円材、支柱、ロッドなどがあります。次の図はアングル ビームを示しています。これは、L 字状に配置された 2 つの細い四角形で断面が構成された一般押し出しです。Extruded Solid ブロックは、L 字形状を断面平面から線形にスイープして、最終的なビームのジオメトリを得ます。
線形スイープとしての一般的な Extruded Solid ブロック
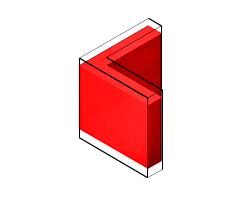
Extruded Solid 形状に関するメモ. Extruded Solid ブロックは、[Regular] 押し出しと呼ばれる別の押し出し形状を提供します。この形状は、[General] 押し出しの簡易版で、各辺の長さが等しい正多角形の断面をもつ固体にのみ適しています。断面の輪郭は多角形の辺の数によって決まっており、穴を含めることはできません。
Revolution Solid ブロックとは
Revolved Solid ブロックは、断面と同じ平面上にある軸を中心とした断面の角スイープを作成する際に使用します。スイープは、1 回転または 0 ~ 360 度の間より小さい角度の範囲で行うことができます。押し出し形状と同様に断面の輪郭は任意で、穴ありにも穴なしにもできます。
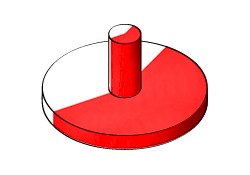
Revolved の例には、円錐、ドーム、ピストン、ギア シャフト、曲がり管などがあります。次の図は円柱ペグを示しています。これは、アングル ビームと同様に L 字状に配置された 2 つの細い四角形で断面が構成された Revolved Solid です。Revolved Solid ブロックは、断面平面上にある軸を中心に L 字形状をスイープし、最終的なペグのジオメトリを得ます。
角スイープとしての Revolved Solid
断面プロファイル
選択した断面の点の座標ペアを入力した MATLAB® 行列により、数値的に断面を指定します。行列の各行は 1 つの点に対する座標ペアを指定します。座標行列の行数に上限はありませんが、閉じた形状を完全に定義するには少なくとも 3 行が必要となります。
% Coordinate Matrix Example: % Square Cross-Section with Center at [0, 0] and Side Length 2 [ -1 -1; % Lower left corner 1 -1; % Lower right corner 1 1; % Upper right corner -1 1; % Upper left corner ]
座標ペアは、押し出し形状の場合は (x, y) 値として扱われ、回転形状の場合は (x, z) 値 (この順序で指定) として扱われます。座標は、(0, 0) のペアが Extruded Solid ブロックまたは Revolved Solid ブロックの基準座標系の原点と一致するように、この座標系で解決されます。一般的な方法は、主要な固体寸法 (半径や長さなど) に関連付けられた MATLAB 変数によって座標をパラメーター化することです。
座標から断面へ
座標ペアは、座標行列内での暗黙的な順序で接続されます。接続は、まっすぐな線分を使用して行われます。その結果として閉じたポリラインができ、材料で埋められる領域 (固体部分) と中空のままの領域 (存在する可能性のある穴と、周囲の空白部分) が隔てられます。
ポリラインに沿って 1 つの点から次の点に進むにつれ、固体領域が左側に、中空領域が右側に広がるように 2 つの領域間の境界が定められます。最初と最後の座標ペアは多くの場合同じですが、そうでない場合は、実際に必ず断面が閉じるよう、間に接続ラインが挿入されます。次のアニメーションによる図解は、穴のないバイナリ リンク断面の描画を示しています。

ポリラインがどこかの点で交差している場合は、断面が無効になることに注意してください。ただし、2 つの線分が互いに近接していたり、一致していたとしても問題ありません。それどころか、この性質を利用して、1 つ以上の穴をもつ断面を指定することもできます。
回転に対する特別な制約
Revolved Solid の座標行列は特別な制約の対象になります。それは、x 座標を負にできないことです。この規則は、Revolved Solid ブロックで使用される回転軸 (z) に一部由来しています。断面をスイープすると、この軸の左側の領域 (負の x 座標をもつ領域) が右側の領域 (正の x 座標をもつ領域) とオーバーラップし、予期しない固体ジオメトリが生成されます。この問題を防ぐため、Revolved Solid の断面に負の x 座標が見つかった場合にはエラーが表示されます。
実践: 単純な断面の定義
図に示された断面について考えます。これは、丸い端部をもつ穴のないバイナリ リンクの断面です。示されている寸法で断面をパラメーター化し、座標行列の形式で指定します。
バイナリ リンクの断面 (穴なし)

はじめに、新しい MATLAB スクリプトを開き、modelParams という名前で任意の場所に保存します。図に示されている長さ (l) と幅 (w) の寸法に用いる、2 つの変数を追加します。長さを 20、幅を 2 に設定します (単位は後で cm になります)。
l = 20;
w = 2; 丸い端部を半円として定義します。まず、左端の角度範囲と右端の角度範囲をもつ 2 つの配列を生成します。これらの配列では、単純な三角関数の式を使用して (x, y) 座標をパラメーター化できます。各配列には 5 つの点がありますが、さらに多くを指定して、より滑らかな形状にすることができます。転置記号 (') によって、A と B が必ず列配列になるようにします。
A = linspace(-pi/2, pi/2, 5)';
B = linspace(pi/2, 3*pi/2, 5)';右端部 (csRight) と左端部 (csLeft) の座標行列を定義します。各行列の最初の列は x 座標に対応します。2 番目の列は y 座標に対応します。2 つの端部の x 座標は、反対方向に l/2 ずつオフセットされます。
csRight = [l/2 + w/2*cos(A) w/2*sin(A)];
csLeft = [-l/2 + w/2*cos(B) w/2*sin(B)];座標行列を結合して cs という名前の単一の行列にします。これは、Revolved Solid ブロックの [Cross-Section] パラメーターで指定しなければならない行列です。断面の直線セグメントは、半円の端点が接続されると自動生成されることに注意してください。
cs = [csRight; csLeft];MATLAB の plot コマンドを使用して、断面の輪郭を可視化できます。次に示すコードを MATLAB コマンド プロンプトで入力してください。
figure; hold on; axis equal; plot(cs(:,1), cs(:,2), 'Color', [0.6 0.6 0.6], 'Marker', '.',... 'MarkerSize', 9, 'MarkerEdgeColor', [1 0 0]);
プロットにバイナリ リンクの断面が表示されます。座標行列内の点は、赤い点で示されています。結果の断面輪郭は、ライト グレーの線で示されています。端部セクションは、それぞれ角度範囲の配列で指定した数である 5 つの点で構成されていることに注意してください。

穴のある断面
座標行列は、常に単一の連続したパスを表している必要があります。この規則は、穴のない断面を指定するときには正しく機能しますが、穴がある場合には特別な注意が必要となります。穴の輪郭は断面の輪郭と連続していないため、この 2 つの間に細い切れ目を追加しなければなりません。この切れ目により、1 つのループで断面と穴の輪郭をすべて通ることができるようになります。
一方の端に穴のあるバイナリ リンクについて考えます。このボディの断面は 2 つの閉じたパスで構成されています。1 つは断面の輪郭のパスで、もう 1 つは穴の輪郭のパスです。パスは物理的に分離しています。しかし、各パスを頂点で切断し、切断された頂点を追加の線分でつなぐことでパスを接続できます。次のアニメーションによる図解は、穴が 1 つあるバイナリ リンク断面の描画を示しています。

このアプローチは、複数の穴をもつ断面に拡張できます。各穴に切れ目がなければならないことに注意してください。切れ目へのアプローチに最適な単独の方法はありません。重要な点は、ポリラインが交差しないようにしながら、断面と穴のすべてを単一の連続したパスで通ることができるようにそれらを計画することです。次のアニメーションによる図解は、穴が 2 つあるバイナリ リンク断面の描画を示しています。

実践: 2 つの穴のある断面の定義
modelParams スクリプトの座標行列を、図に示すようなまったく同じ 2 つの穴を含めるように変更します。作業中はスクリプトを頻繁に保存してください。
バイナリ リンクの断面 (2 つ穴)

はじめに、穴の直径用に新しい変数 (d) を追加します。直径を 1.2 に設定します (単位は後で cm になります)。
d = 1.2;左右の穴用に新しい角度範囲の配列を生成します。左右の穴は同じ順序で描画されるため、1 つの配列で済みます。配列の要素は時計回りの順序になっているため、断面を生成するときに固体領域が必ず左側になります。配列の要素数は、穴の角度範囲が広くなった (180° に対し 360°) ことが反映されるよう、倍になっています。
C = linspace(3*pi/2, -pi/2, 10)';左の穴 (csLeftHole)、右の穴 (csRightHole)、およびその 2 つの間の接続ライン (csConnLine) の輪郭を定義します。x 座標は、左の穴については、その長さの半分 (l/2) だけ左にシフトし、右の穴については、それと同じ距離だけ右にシフトします。
csLeftHole = [-l/2 + d/2*cos(C) d/2*sin(C)];
csRightHole = [+l/2 + d/2*cos(C) d/2*sin(C)];
csConnLine = [-l/2 -w/2; +l/2 -w/2];新しい座標行列を既存の cs 行列に追加します。行列の順序によって、断面全体が描画される順序が決定されます。結果は、Revolved Solid ブロックの [Cross-section] パラメーターで指定できる変数になります。
cs = [csRight; csLeft; csLeftHole; ...
csConnLine; csRightHole];前述のように、断面の輪郭は MATLAB の plot コマンドを使用して可視化できます。必ず、以下に示すプロット用コードがスクリプトに含まれるようにしてください。その後、スクリプトを実行してプロットを生成します。
figure; hold on; axis equal; plot(cs(:,1), cs(:,2), 'Color', [0.6 0.6 0.6], 'Marker', '.',... 'MarkerSize', 9, 'MarkerEdgeColor', [1 0 0]);
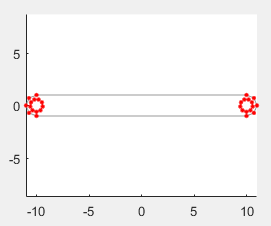
プロットにバイナリ リンクの断面が表示されます。座標行列内の点は、赤い点で示されています。結果の断面輪郭は、ライト グレーの線で示されています。穴セクションは、それぞれ、角度範囲の配列で指定した数である 10 個の点で構成されていることに注意してください。
断面から固体へ
基準座標系の z 軸は、Extruded Solid ブロックと Revolved Solid ブロックの両方で、スイープ軸として機能します。Extruded Solid ブロックの場合はこの軸に沿って、Revolved Solid ブロックの場合はこの軸を中心に、指定した断面がスイープされます。スイープは、断面平面に対して対称になります。つまり、スイープ長またはスイープ角度の半分のスイープが、スイープ軸からそれぞれの方向に向けて実行されます。この対称性により、断面平面は (したがって基準座標系の原点は) スイープの終点間の中間に維持されます。
実践: 断面を使用した固体のモデル化
新しい Simulink® モデルを開き、Bodies ライブラリから Extruded Solid ブロックを追加します。モデル キャンバスをクリックし、ブロック名を入力して、表示されたオプションから選択することができます。モデルを任意の場所に
binaryLinkSolidとして保存します。Extruded Solid ブロックのダイアログ ボックスで、[Geometry] パラメーターを次の表のとおりに設定します。パラメーターの単位を
cmに設定します。[Cross-Section] パラメーターは、modelParamsスクリプトでcs変数によって定義されます。パラメーター 値 Cross-Section csLength 1 モデル ワークスペースに
modelParamsスクリプトを読み込みます。[モデル化] タブで、[モデル エクスプローラー] をクリックします。このツールを使用して、以前に作成した
modelParamsスクリプトをモデル ワークスペースに読み込みます。[モデルの階層構造] ペインで、モデル ([binaryLinkSolid]) に対応するノードを展開し、[モデル ワークスペース] を選択します。
[モデル ワークスペース] ペインで、[データ ソース] パラメーターを
[MATLAB ファイル]に設定し、modelParamsのスクリプトを参照します。[ソースから再初期化] ボタンをクリックして、スクリプトで定義された変数を読み込みます。
Extruded Solid ブロックのダイアログ ボックスで、[Update Visualization] ボタン
 をクリックします。可視化ペインが更新され、最終的な固体ジオメトリが表示されます。
をクリックします。可視化ペインが更新され、最終的な固体ジオメトリが表示されます。 [Fit to View] ボタンをクリックして、可視化ペインのサイズに合わせてバイナリ リンクをスケーリングします。[Toggle visibility of frames] ボタンをクリックして、固体の基準座標系を表示します。基準座標系の原点は断面座標の [0, 0] と一致し、押し出しの終端の中間に配置されています。
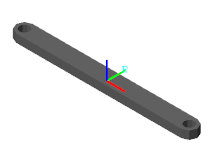
丸い端部と穴の外観がギザギザになっていることに注意してください。この効果は、座標行列の丸い部分、
csLeftEnd、csRightEnd、csLeftHole、およびcsRightHoleに使用されている点の数が少ないことに起因します。より滑らかなジオメトリを得るには、角度範囲の行列の要素数を増やします。
