陰的なソルバーに対するヤコビ メソッドの選択

陰的なソルバーに対し、Simulink^® では "ソルバーのヤコビアン" を計算しなければなりません。これは、Simulink モデルの連続表現に関連付けられているヤコビ行列の部分行列です。一般的に、この連続表現の形式は次のようになります。

$$\begin{array}{l}\dot{x}=f(x,t,u)\\ y=g(x,t,u).\end{array}$$

この方程式系から形成されるヤコビアン J は次のとおりです。

$$J=\left(\begin{array}{cc}\frac{\partial f}{\partial x}& \frac{\partial f}{\partial u}\\ \frac{\partial g}{\partial x}& \frac{\partial g}{\partial u}\end{array}\right)=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right).$$

これにより、ソルバーのヤコビアンは部分行列 $$J_x$$ になります。

$$J_x=A=\frac{\partial f}{\partial x}.$$

ヤコビアンのスパース性

多くの物理システムでは、ソルバーのヤコビアン J_x は "スパース"、つまり、 J_x の多くの要素はゼロになっています。

次の方程式系を考えます。

$$\begin{array}{l}{\dot{x}}_1=f_1(x_1,x_3)\\ {\dot{x}}_2=f_2(x_2)\\ {\dot{x}}_3=f_3(x_2).\end{array}$$

このシステムからは、方程式の構造を反映したスパース パターンを導出できます。このパターンの boolean 行列は、方程式の右側に明示的に表示される各 $$x_i$$ に対し、1 の値をもっています。したがって、次が得られます。

$$J_{x,pattern}=\left(\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 0& 1& 0\end{array}\right)$$

スパース摂動法とスパース解析法は、このスパース パターンを利用して必要な計算数を削減し、パフォーマンスを向上できる場合があります。

ソルバーのヤコビ メソッド

[コンフィギュレーション パラメーター] ダイアログ ボックスの [ソルバー] ペインで陰的ソルバーを選択すると、[ソルバーのヤコビ メソッド] というパラメーターとドロップダウン メニューが表示されます。このメニューには、ソルバーのヤコビアンを計算する際のオプションが 5 つあります。

メモ

[診断] ペインの [ソルバー] セクションで [自動ソルバー パラメーターの選択] を [エラー] に設定し、Simulink が推奨するソルバーとは異なるソルバーを選択すると、エラーが表示される場合があります。

制限

ソルバーのヤコビ メソッドには次の制限が伴います。

• 解析的ヤコビ メソッドが選択されていてもモデル内の 1 つ以上のブロックに解析的なヤコビアンがない場合、Simulink は摂動法を適用します。

• スパース摂動を選択し、モデルにデータ ストア ブロックが含まれている場合は、Simulink によってフル摂動法が適用されます。

ヒューリスティックな [自動] 方法

[Solver Jacobian method] の既定の設定は [自動] です。この項目を選択すると、Simulink では 4 つの残りのメソッドのいずれがモデルに最適であるかを判断します。このフローチャートはアルゴリズムを表現しています。

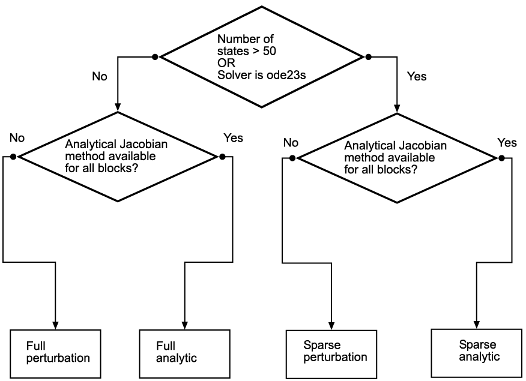
スパース法は多数の状態をもつモデルにとって有益です。モデルに 50 以上の状態が存在する場合は、[自動] によってスパース法が選択されます。他の陰的なソルバーとは異なり、タイム ステップごとに新しいヤコビアンを生成するため、ode23s はスパース法です。したがって、スパース解析法またはスパース摂動法は効果的です。[自動] を選択することで、モデル内の各ブロックが解析ヤコビアンを生成できる場合にのみ、解析的手法が使用されるようになります。

フル摂動法とスパース摂動法

フル摂動法は摂動方程式の完全なセットを解き、線形代数演算に LAPACK を使用します。この方法は、計算の観点から見るとコストが高くなりますが、ベースライン結果を確立するための推奨される方法となっています。

スパース摂動法では、スパースなヤコビアンのパターンを数学的に利用して、実行時の性能を向上させます。3 つの方程式と 3 つの状態のサンプル システムに戻ります。

$$\begin{array}{l}{\dot{x}}_1=f_1(x_1,x_3)\\ {\dot{x}}_2=f_2(x_2)\\ {\dot{x}}_3=f_3(x_2).\end{array}$$

ソルバーのヤコビアンは次のとおりです。

$$\begin{array}{c}{J}_x=\left(\begin{array}{ccc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& \frac{\partial f_1}{\partial x_3}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& \frac{\partial f_2}{\partial x_3}\\ \frac{\partial f_3}{\partial x_1}& \frac{\partial f_3}{\partial x_2}& \frac{\partial f_3}{\partial x_3}\end{array}\right)\\ =\left(\begin{array}{ccc}\frac{f_1(x_1+\Delta x_1,x_2,x_3)-f_1}{\Delta x_1}& \frac{f_1(x_1,x_2+\Delta x_2,x_3)-f_1}{\Delta x_2}& \frac{f_1(x_1,x_2,x_3+\Delta x_3)-f_1}{\Delta x_3}\\ \frac{f_2(x_1+\Delta x_1,x_2,x_3)-f_2}{\Delta x_1}& \frac{f_2(x_1,x_2+\Delta x_2,x_3)-f_2}{\Delta x_2}& \frac{f_2(x_1,x_2,x_3+\Delta x_3)-f_2}{\Delta x_3}\\ \frac{f_3(x_1+\Delta x_1,x_2,x_3)-f_3}{\Delta x_1}& \frac{f_3(x_1,x_2+\Delta x_2,x_3)-f_3}{\Delta x_2}& \frac{f_3(x_1,x_2,x_3+\Delta x_3)-f_3}{\Delta x_3}\end{array}\right)\end{array}$$

したがって、3 つの各状態に摂動を 3 回与え、導関数を 3 回評価することが必要になります。n 個の状態をもつシステムでは、状態に n 回摂動が与えられます。

スパース パターンを適用し、状態 x₁ および x ₂ に共に摂動を与えると、この行列は次のように縮小されます。

$$J_x=\left(\begin{array}{ccc}\frac{f_1(x_1+\Delta x_1,x_2+\Delta x_2,x_3)-f_1}{\Delta x_1}& 0& \frac{f_1(x_1,x_2,x_3+\Delta x_3)-f_1}{\Delta x_3}\\ 0& \frac{f_2(x_1+\Delta x_1,x_2+\Delta x_2,x_3)-f_2}{\Delta x_2}& 0\\ 0& \frac{f_3(x_1+\Delta x_1,x_2+\Delta x_2,x_3)-f_3}{\Delta x_2}& 0\end{array}\right)$$

これでソルバーは、1 回のスイープで列 1 と列 2 を解くことができるようになりました。スパース摂動法では計算量が大幅に節約されますが、コンパイルのオーバーヘッドも増加します。システムに多数の連続状態が含まれていない場合は、シミュレーションの速度が遅くなる場合もあります。この方法を適用することで性能が向上する分岐点が存在します。一般的に、多数の連続状態をもつシステムは通常はスパースであるため、スパース法が適しています。

スパース摂動法では、スパース解析法と同様に、UMFPACK を使用して線形代数演算を実行します。また、スパース摂動法は、RSim およびラピッド アクセラレータ モードの両方をサポートしています。

フル解析法とスパース解析法

フル解析法とスパース解析法では、摂動方程式の代わりに解析方程式を使用してヤコビアンを計算することで、性能を向上させます。またスパース解析法ではスパース情報を使用して、常微分方程式を解くのに必要な線形代数演算を高速化します。

MATLAB^® でのスパース パターンへのアクセスと解釈の方法の詳細については、モデルのソルバー ヤコビ行列構造の探索を参照してください。

コード生成のサポート

スパース摂動法は RSim をサポートしていますが、スパース解析法ではサポートしていません。その結果、選択したスパース法にかかわらず、生成されたコードではスパース摂動法が使用されます。この制限は、ラピッド アクセラレータ モードにも適用されます。