このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

Hampel 識別子を使用した外れ値の排除

この例では、hampel が、外れ値の検出と削除に使用する手順をナイーブに実行する方法について説明します。実際の関数は、はるかに高速です。

24 個のサンプルを含むランダム信号 x を生成します。再現可能な結果が必要な場合は、乱数発生器をリセットします。

rng default

lx = 24;
x = randn(1,lx);

x の各要素を囲む観測ウィンドウを生成します。サンプルの両側に k = 2 個の近傍を取ります。結果として得られた移動ウィンドウの長さは、$$2\times 2+1=5$$ サンプルです。

k = 2;

iLo = (1:lx)-k;
iHi = (1:lx)+k;

ウィンドウを打ち切り、信号のエッジが近づくにつれて関数がより小さなセグメントの中央値を計算するようにします。

iLo(iLo<1) = 1;
iHi(iHi>lx) = lx;

周囲の各ウィンドウの中央値を記録します。ウィンドウの中央値に対する各要素の絶対偏差の中央値を探します。

for j = 1:lx
    w = x(iLo(j):iHi(j));
    medj = median(w);
    mmed(j) = medj;
    mmad(j) = median(abs(w-medj));
end

以下によって、中央絶対偏差をスケーリングします。

$$\frac{{\displaystyle 1}}{{\displaystyle \sqrt{2}{erf}^{-1}(1/2)}}\approx 1.4826$$

これにより、正規分布の標準偏差の推定値が取得されます。

sd = mmad/(erfinv(1/2)*sqrt(2));

中央値から nd = 2 の標準偏差より大きく離れているサンプルを探します。これらの各外れ値を、それを囲むウィンドウの中央値に置き換えます。これが、Hampel アルゴリズムの本質です。

nd = 2;
ki = abs(x-mmed) > nd*sd;

yu = x;
yu(ki) = mmed(ki);

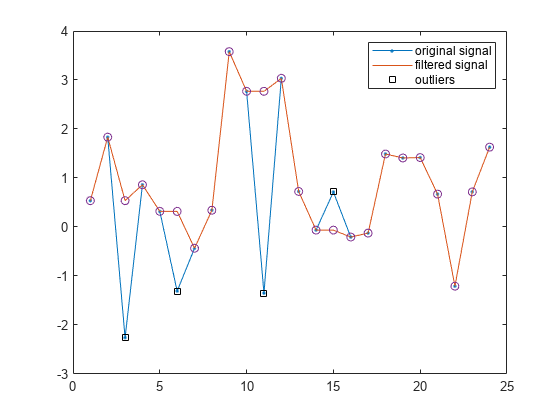
関数 hampel を使用し、フィルター処理した信号を計算して、外れ値に注釈を付けます。この例で計算したフィルター処理済みの値を重ね合わせます。

hampel(x,k,nd)

hold on
plot(yu,'o','HandleVisibility','off')
hold off

参考

hampel