余弦波の解析信号
この例では、解析信号を求める方法を示します。この例ではまた、余弦波に対応する解析信号の虚数部は同じ周波数をもつ正弦波であることも説明します。この余弦波の平均が非ゼロ (DC シフト) の場合、解析信号の実数部は同じ平均をもつ元の余弦波ですが、虚数部はゼロ平均です。
周波数 100 Hz の余弦波を作成します。サンプル レートは 10 kHz です。余弦波に 2.5 の DC オフセットを加算します。
t = 0:1e-4:1; x = 2.5 + cos(2*pi*100*t);
関数 hilbert を使用して解析信号を求めます。実数部は元の信号と同じです。虚数部は元の信号のヒルベルト変換です。比較のために、実数部と虚数部をプロットします。
y = hilbert(x); plot(t,real(y)) hold on plot(t,imag(y)) xlim([0 0.1]) grid on text([0.015 0.015],[3.7 1.2], ... {'Real Part \downarrow';'Imaginary Part \downarrow'})
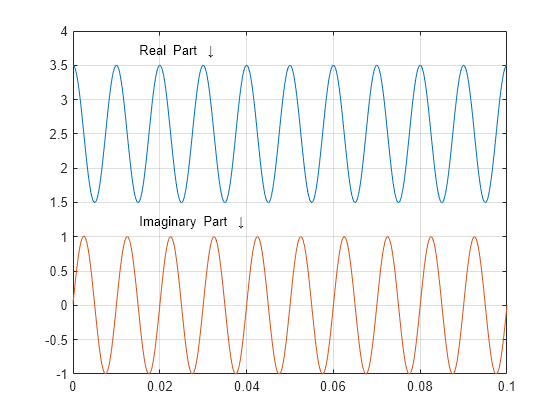
虚数部は、余弦波の実数部と同じ周波数をもつ正弦波であることがわかります。ただし、虚数部は平均 0 をもち、実数部は平均 2.5 をもちます。
元の信号は以下で表されます。
結果として得られる解析信号は次のようになります。
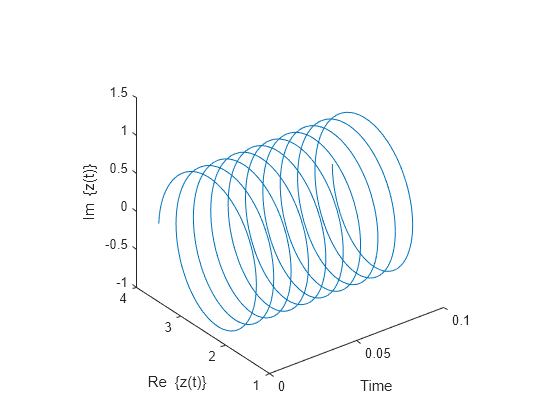
複素数値の解析信号を 10 周期プロットします。
prds = 1:1000; figure plot3(t(prds),real(y(prds)),imag(y(prds))) xlabel('Time') ylabel('Re \{z(t)\}') zlabel('Im \{z(t)\}') axis square