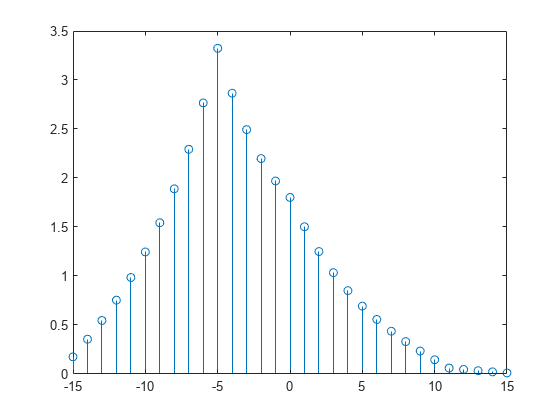
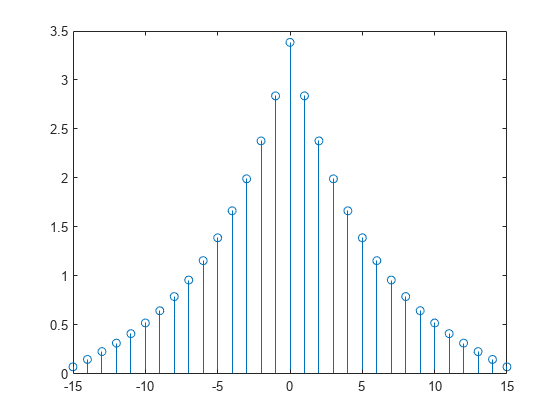
xcorr
相互相関
説明
例
入力引数
出力引数
詳細
参照
[1] Buck, John R., Michael M. Daniel, and Andrew C. Singer. Computer Explorations in Signals and Systems Using MATLAB®. 2nd Edition. Upper Saddle River, NJ: Prentice Hall, 2002.
[2] Stoica, Petre, and Randolph Moses. Spectral Analysis of Signals. Upper Saddle River, NJ: Prentice Hall, 2005.