等間隔でサンプリングされている信号のリサンプリング
この例では、等間隔でサンプリングされた信号を別の等間隔のレートでリサンプリングする方法を説明します。ここでは、大きな過渡特性の影響を低減する方法および望ましくない高周波数成分を除去する方法を説明します。
有理因数によるレート変換
関数 resample は、あるサンプル レートから別のサンプル レートへの変換を実行します。resample では、整数の因数 p でアップサンプリングし、続いて別の整数の因数 q で間引きできます。この方法では、元のサンプル レートの有理数の倍数 (p / q) でリサンプリングできます。
等間隔のサンプルに対して関数 resample を使用するには、この有理因数の分子係数と分母係数の両方を与えなければなりません。必要な整数を決定するには、関数 rat を使用できます。
以下は、48 kHz から 44.1 kHz へ変換する場合に rat を呼び出す方法の例です。
originalFs = 48000; desiredFs = 44100; [p,q] = rat(desiredFs / originalFs)
p = 147
q = 160
rat は、147 でアップサンプリングして 160 で間引きできることを示しています。これで目的のレートになるかどうかを検証するには、次のように p / q を元のサンプル レートで乗算します。
originalFs * p / q
ans = 44100
新しいサンプル レートと元のサンプル レートの比率が得られたら、resample を呼び出すことができます。
たとえば、次のように元の 48 kHz のサンプル レートを使用して長さ 10 ms の 500 Hz 正弦波を作成し、それを 44.1 kHz に変換します。
tEnd = 0.01; Tx = 0:1/originalFs:tEnd; f = 500; x = sin(2*pi*f*Tx); y = resample(x,p,q); Ty = (0:numel(y)-1)/desiredFs; plot(Tx,x,". ") hold on plot(Ty,y,"o ") hold off legend("Original","Resampled")
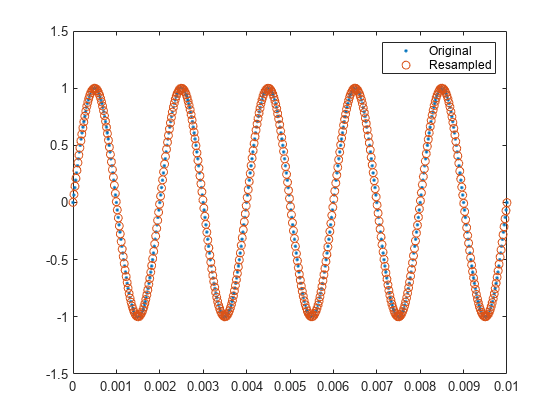
上記の正弦波のように整った動作の信号の場合、注意して選択した p および q を指定して resample を使用するだけで、正しく再構成されるはずです。
過渡特性または著しいノイズのある信号では、resample 内のポリフェーズ アンチエイリアシング フィルターをより厳密に制御する必要が生じる場合もあります。
過渡特性のフィルター処理
関数 resample では、レート変換時にフィルターを使用します。このフィルター処理は信号の大きな過渡特性の影響を大きく受けます。
矩形パルスをリサンプリングしてこれを説明します。
x = [zeros(1,120) ones(1,241) zeros(1,120)]; y = resample(x,p,q); plot(Tx,x,"-", Ty,y,"-") legend("Original","Resampled")
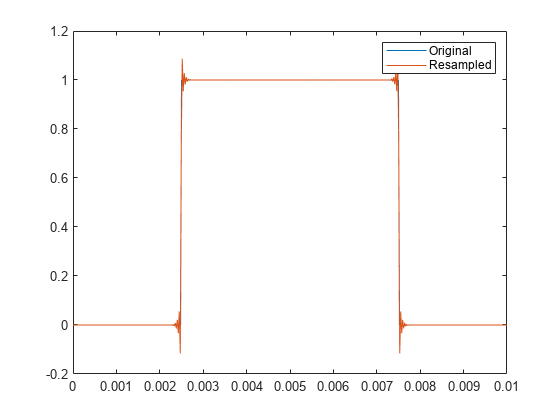
この関数は、パルスの平坦な領域については再構成を適切に行うことができます。しかし、このパルスのエッジにはスパイクがあります。
次のように、最初のパルスのエッジにズームインします。
xlim([2e-3 3e-3])
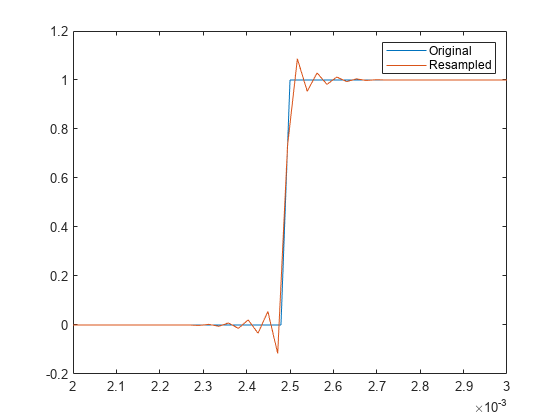
遷移領域に減衰振動があります。内部フィルターの設定を調整することで、この振動を抑えることができます。
resample では、エッジの影響をある程度軽減可能なアンチエイリアシング フィルターに適用するカイザー ウィンドウを制御できます。
2 つのパラメーター n および beta は、フィルターの相対的な長さとフィルターが試行する平滑化の量を制御します。n の値が大きいと、フィルター長は長くなります。beta が 0 の場合、平滑化は行われません。beta の値が大きいと、平滑化の量が大きくなります。既定の設定では、n は 10 で beta は 5 です。
実際に行う際には、既定の値から始めて必要に応じて調整してください。ここでは、n を 5、beta を 20 に設定します。
n = 5; beta = 20; y = resample(x,p,q,n,beta); plot(Tx,x,".-") hold on plot(Ty,y,"o-") hold off legend("Original","Resampled") xlim([2e-3 3e-3])
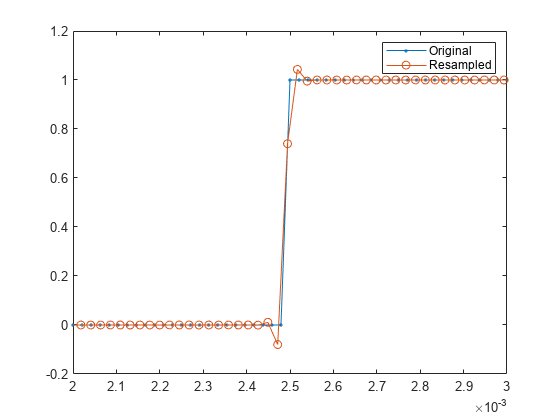
振動が大幅に減少しています。
エイリアスのフィルター処理
関数 resample は、サンプル レートをより高く、あるいはより低く変換するように設計されています。そのため、アンチエイリアシング フィルターの周波数のカットオフは、入力または出力 (どちらか低い方) のサンプル レートのナイキスト周波数に設定されています。この既定の設定により、関数 resample はさまざまな用途に利用できます。
フィルターを直接制御すると有益な場合があります。
これを説明するため、96 kHz でサンプリングされたチャープ信号のスペクトログラムを構成して表示します。チャープ信号は、0 Hz から 48 kHz のナイキスト範囲全体で 8 秒間にわたって周波数が二次的に変化する正弦波で構成されています。
fs1 = 96000; t1 = 0:1/fs1:8; x = chirp(t1, 0, 8, fs1/2, "quadratic"); spectrogram(x,kaiser(256,15),220,412,fs1,"yaxis")
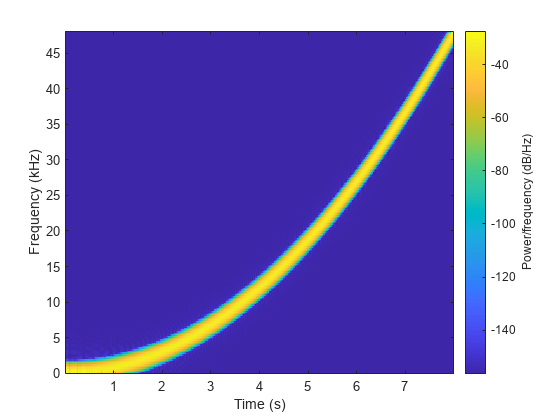
次に、resample の既定の設定を使用してチャープを 44.1 kHz に変換し、スペクトログラムを表示します。
fs2 = 44100;
[p,q] = rat(fs2/fs1);
y = resample(x,p,q);
spectrogram(y,kaiser(256,15),220,412,fs2,"yaxis")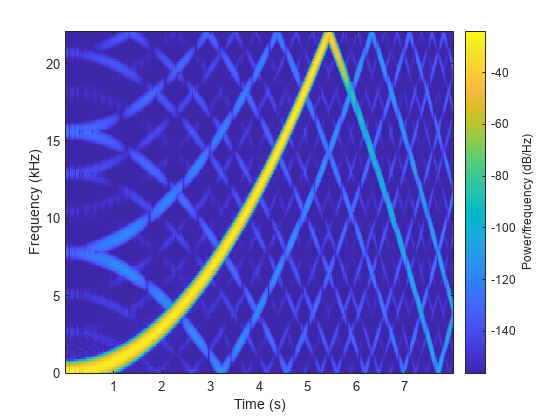
ここでは、元の信号だけでなく、望ましくない周波数成分も確認できます。正弦波は、0 Hz で始まり 5.422 秒で 22.05 kHz のナイキスト周波数に達するまで続くのが理想的です。しかし、リサンプリングに使用した既定のフィルターのエッジで発生した小さな不連続部分が原因となり、アーティファクトが生じています。これらのアーティファクトを防ぐには、既定のフィルターよりカットオフ周波数がわずかに低く、阻止帯域の抑制量が大きい、長めのフィルターを使用します。
適切に時間調整するために、フィルターは奇数長である必要があります。長さは p または q (大きい方) の数倍でなければなりません。同様に、目的の正規化カットオフ周波数を p または q のいずれか大きい方で除算します。いずれの場合にも、結果として得られる係数を p で乗算します。
以下は、出力されるナイキスト周波数の 98% (0.98) をカットオフし、間引き係数の 256 倍の次数をもち、12 の beta でカイザー ウィンドウを適用されるフィルターの例です。
normFc = .98 / max(p,q); order = 256 * max(p,q); beta = 12; lpFilt = firls(order, [0 normFc normFc 1],[1 1 0 0]); lpFilt = lpFilt .* kaiser(order+1,beta)'; lpFilt = lpFilt / sum(lpFilt); % multiply by p lpFilt = p * lpFilt; % resample and plot the response y = resample(x,p,q,lpFilt); spectrogram(y,kaiser(256,15),220,412,fs2,"yaxis")

エイリアスが除去されていることに注意してください。
参考情報
リサンプリングについての詳細については、マルチレート信号処理を参照してください。
参考文献: fredric j harris, "Multirate Signal Processing for Communications Systems", Prentice Hall, 2004.