Tire-Road Interaction (Magic Formula)

Tire-road dynamics given by Magic Formula coefficients

• 

Libraries:
Simscape / Driveline / Tires & Vehicles / Tire Subcomponents

Description

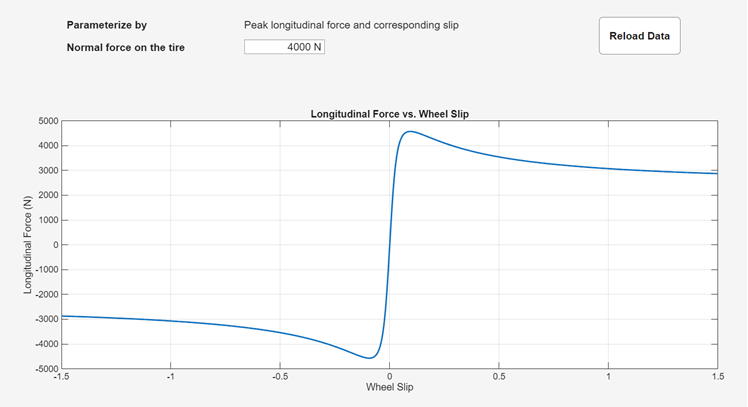
The Tire-Road Interaction (Magic Formula) block represents the interaction between the tire tread and the road pavement. The Magic Formula predicts the longitudinal force that results from this interaction by using an empirical equation based on fitting coefficients. The block ignores tire properties such as compliance and inertia.

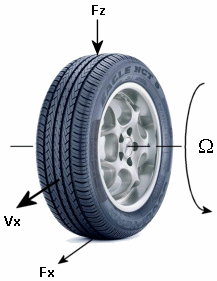
Tire-Road Interaction Model

The block represents the longitudinal forces at the tire-road contact patch using the Magic Formula of Pacejka [2].

The figure displays the forces on the tire. The table defines the tire model variables.

Symbol	Description
Ω	Wheel angular velocity.
rw	Wheel radius.
Vx	Wheel hub longitudinal velocity.
$$r_w\Omega$$	Tire tread longitudinal velocity.
u	Tire longitudinal deformation.
$$V_T=r_w{\Omega }^{\prime }=r_w\Omega +\dot{u}$$	Tire tread longitudinal velocity. Typically, the tire tread longitudinal velocity has a component due to tire rotation, rwΩ, and an optional component due to tire deformation, $$\dot{u}$$. Because port T computes VT, the calculations for tire rotations and deformation occur outside of the block.
$$V_{sx}=V_x-V_T$$	Contact patch slip velocity. If there is no tire longitudinal compliance, then $$u=0$$.
$$k=-\frac{V_{sx}}{{\left|V_x\right|}_{smooth}}$$	Wheel slip for a tire without compliance.
Fz	Vertical load on tire.
Fz0	Nominal vertical load on tire.
$$F_x=f(k,F_z)$$	Longitudinal force exerted on the tire at the contact point. f is a characteristic function of the tire.

Tire Response

You can model tire roll and slip.

Forces and Characteristic Function

The block uses a steady-state tire characteristic function, $$F_x=f(k,F_z)$$, where:

• F_x is the longitudinal force on the tire.

• F_z is the vertical load.

• k is the wheel slip

Roll and Slip

The equation for translational motion of a non-slipping, non-compliant tire is $$V_x=r_w\Omega$$. When tires experience slip, they develop a longitudinal force, F_x.

The contact patch slip velocity is $$V_{sx}=V_x-r_w\Omega -\dot{u}$$. For a tire without compliance, u = 0. The unsmoothed contact patch slip is

$$k=-\frac{V_{sx}}{\left|V_x\right|},$$

and the block saturates the slip denominator as

$$\left|V_x\right|=\{\begin{array}{ll}{V}_{XLOW}\hfill & \text{if }\left|V_x\right|<V_{XLOW}\hfill \\ \left|V_x\right|\hfill & \text{otherwise}\hfill \end{array}$$

where V_XLOW is the Lower boundary of slip denominator, VXLOW parameter. The block smoothly transitions |V_x| to V_XLOW over the transition regions -V_XLOW - V_th/2 < V_x < -V_XLOW + V_th/2 and V_XLOW - V_th/2 < V_x < V_XLOW + V_th/2. The block saturates slip according to

$$k=\{\begin{array}{ll}kpumin\hfill & \text{if }-\frac{V_{sx}}{\left|V_x\right|}<kpumin\hfill \\ kpumax\hfill & \text{if }-\frac{V_{sx}}{\left|V_x\right|}>kpumax\hfill \\ -\frac{V_{sx}}{\left|V_x\right|}\hfill & \text{otherwise}\hfill \end{array}$$

where kpumin is the Minimum valid wheel slip, KPUMIN parameter and kpumax is the Maximum valid wheel slip, KPUMAX parameter. The block transitions k over the regions kpumin - k_th/2 < k < kpumin + k_th/2 and kpumax - k_th/2 < k < kpumax + k_th/2. The block defines the slip smoothing threshold as

$$k_{th}=\frac{V_{th}}{1m/s}.$$

For this equation, a locked, sliding wheel has k = -1. For perfect rolling, k = 0.

Magic Formula Coefficients for Typical Road Conditions

The block uses numerical values based on empirical tire data. These values are typical sets of constant Magic Formula coefficients for common road conditions.

Surface	B	C	D	E
Dry tarmac	10	1.9	1	0.97
Wet tarmac	12	2.3	0.82	1
Snow	5	2	0.3	1
Ice	4	2	0.1	1

Parameterizations

Peak Longitudinal Force and Corresponding Slip

When you set Parameterize by to Peak longitudinal force and corresponding slip, the block uses a representative set of Magic Formula coefficients. The block scales the coefficients to yield the peak longitudinal force F_x0 at the corresponding slip κ₀ that you specify, for rated vertical load F_z0.

Magic Formula with Constant Coefficients

When you set Parameterize by to Constant Magic Formula coefficients, the block uses the dimensionless coefficients, B, C, D, and E, or stiffness, shape, peak, and curvature, such that

$$F_x=f(\kappa ,F_z)=F_z\cdot D\cdot \sin \left(C\cdot \arctan \left\{B\kappa -E\left[B\kappa -\arctan \left(B\kappa \right)\right]\right\}\right).$$

The slope of f at $$k=0$$ is $$BCD\cdot F_z$$.

Magic Formula with Load-Dependent Coefficients

When you set Parameterize by to Load-dependent Magic Formula coefficients, the block uses dimensionless coefficients that are functions of the tire load. A more complex set of parameters p_i, entered in the property inspector, specifies these functions:

$$F_{x0}=D_x\sin \left(C_x\arctan \left\{B_x{\kappa }_x-E_x\left[B_x{\kappa }_x-\arctan \left(B_x{\kappa }_x\right)\right]\right\}\right)+S_{Vx},$$

where:

$$d{f}_{\text{z}}=\frac{\left(F_{\text{z}}–F_{\text{z}0}\right)}{F_{\text{z0}}}$$

$${\kappa }_{{}_x}=\kappa +S_{{}_{Hx}}$$

$$C_{\text{x}}=\text{ p}\_\text{Cx1}$$

$$D_{\text{x}}={\mu }_{\text{x}}·F_{\text{z}}$$

$${\mu }_{\text{x}}=\text{ p}\_\text{Dx1 }+\text{ p}\_\text{Dx2}·d{f}_{\text{z}}$$

$$E_{\text{x}}=\left(\text{p}\_\text{Ex1 }+\text{ p}\_\text{Ex2}·d{f}_{\text{z}}+\text{ p}\_\text{Ex3}·d{f}_{\text{z}}{}^{\text{2}}\right)\left[\text{1 }–\text{ p}\_\text{Ex4}·\text{sgn}\left({\kappa }_{\text{x}}\right)\right]$$

$$K_{\text{x}\kappa }=F_{\text{z}}\cdot \left(\text{p}\_\text{Kx1 }+\text{ p}\_\text{Kx2}·d{f}_{\text{z}}\right)\cdot e^{\left(\text{p}\_\text{Kx3}·d{f}_{\text{z}}\right)}$$

$$B_{\text{x}}=\frac{K_{\text{x}\kappa }}{C_{\text{x}}{D}_{\text{x}}+{\epsilon }_{\text{x}}}$$

$$S_{\text{Hx}}=\text{ p}\_\text{Hx1 }+\text{ p}\_\text{Hx2}·d{f}_{\text{z}}$$

$$S_{\text{Vx}}=F_{\text{z}}·\left(\text{p}\_\text{Vx1 }+\text{ p}\_\text{Vx2}·d{f}_{\text{z}}\right)$$

S_Hx and S_Vx represent offsets to the slip and longitudinal force in the force-slip function, or horizontal and vertical offsets if the function is plotted as a curve. μ_x is the longitudinal load-dependent friction coefficient. ε_x is a small number that prevents division by zero as F_z approaches zero.

Assumptions and Limitations

The Tire-Road Interaction (Magic Formula) block assumes only longitudinal motion and includes no camber, turning, or lateral motion.

Ports

Input

N — Normal force, N

physical signal

Physical signal input port associated with the normal force acting on the tire, in N. The normal force is positive if it acts downward on the tire, pressing it against the pavement.

M — Magic formula coefficients, unitless

physical signal | vector

Physical signal input port associated with the Magic Formula coefficients. Provide the Magic Formula coefficients as a four-element vector specified in the order [B, C, D, E].

Dependencies

To enable this port, set Parameterize by to Physical signal Magic Formula coefficients.

Output

S — Slip

physical signal

Physical signal output port associated with the relative slip, k, between the tire and road.

Conserving

T — Tire tread

mechanical rotational

Mechanical rotational port associated with the tire tread.

H — Hub

mechanical translational

Mechanical translational port associated with the wheel hub that transmits the thrust generated by the tire to the remainder of the vehicle.

Parameters

Main

Parameterize by — Parameterization method

Peak longitudinal force and corresponding slip (default) | Constant Magic Formula coefficients | Load-dependent Magic Formula coefficients | Physical signal Magic Formula coefficients

Magic Formula tire simulation option. Select how the block parameterizes the tire using the Magic Formula:

• Peak longitudinal force and corresponding slip — Parameterize the Magic Formula by using the physical characteristics of the tire.

• Constant Magic Formula coefficients — Specify the parameters that define the constant B, C, D, and E coefficients as scalars.

• Load-dependent Magic Formula coefficients — Specify the parameters that define the load-dependent C, D, E, K, H, and V coefficients as vectors, one for each coefficient.

• Physical signal Magic Formula coefficients — Specify the Magic Formula coefficients using port M as a four-element vector in the order [B, C, D,E].

Rated vertical load — Rated load force

3000 N (default) | positive scalar

Rated vertical load force F_z0.

Dependencies

To enable this parameter, set Parameterize by to Peak longitudinal force and corresponding slip.

Peak longitudinal force at rated load — Maximum longitudinal force at rated load

3500 N (default) | positive scalar

Maximum longitudinal force F_x0 that the tire exerts on the wheel when the vertical load equals its rated value F_z0.

Dependencies

To enable this parameter, set Parameterize by to Peak longitudinal force and corresponding slip.

Slip at peak force at rated load (percent) — Percent slip at maximum longitudinal force and rated load

10 (default) | positive scalar

Contact slip κ'₀, expressed as a percentage (%), when the longitudinal force equals its maximum value F_x0 and the vertical load equals its rated value F_z0.

Dependencies

To enable this parameter, set Parameterize by to Peak longitudinal force and corresponding slip.

Magic Formula B coefficient — Constant Magic Formula B coefficient

10 (default) | positive scalar

Load-independent Magic Formula B coefficient.

Dependencies

To enable this parameter, set Parameterize by to Constant Magic Formula coefficients.

Magic Formula C coefficient — Constant Magic Formula C coefficient

1.9 (default) | positive scalar

Load-independent Magic Formula C coefficient.

Dependencies

To enable this parameter, set Parameterize by to Constant Magic Formula coefficients.

Magic Formula D coefficient — Constant Magic Formula D coefficient

1 (default) | positive scalar

Load-independent Magic Formula D coefficient.

Dependencies

To enable this parameter, set Parameterize by to Constant Magic Formula coefficients.

Magic Formula E coefficient — Constant Magic Formula E coefficient

0.97 (default) | positive scalar

Load-independent Magic Formula E coefficient.

Dependencies

To enable this parameter, set Parameterize by to Constant Magic Formula coefficients.

Tire nominal vertical load, FNOMIN — Normal force

4000 N (default) | positive scalar

Nominal normal force F_z0 on tire.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula C-coefficient parameter, p_Cx1 — Variable Magic Formula C coefficient

1.685 (default) | scalar

Load-dependent Magic Formula C coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula D-coefficient parameters, [p_Dx1 p_Dx2] — Variable Magic Formula D coefficient

[1.21, -.037] (default) | vector

Load-dependent Magic Formula D coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula E-coefficient parameters, [p_Ex1 p_Ex2 p_Ex3 p_Ex4] — Variable Magic Formula E coefficient

[.344, .095, -.02, 0] (default) | vector

Load-dependent Magic Formula E coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula BCD-coefficient parameters, [p_Kx1 p_Kx2 p_Kx3] — Variable Magic Formula K coefficient

[21.51, -.163, .245] (default) | vector

Load-dependent Magic Formula K coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula H-coefficient parameters, [p_Hx1 p_Hx2] — Variable Magic Formula H coefficient

[-.002, .002] (default) | vector

Load-dependent Magic Formula H coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula V-coefficient parameters, [p_Vx1 p_Vx2] — Variable Magic Formula V coefficient

[0, 0] (default) | vector

Load-dependent Magic Formula V coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Scaling

Enable scaling coefficients — Scaling option

off (default) | on

Whether to include scaling coefficients in the Magic Formula parameterization.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Scale factor of Fx nominal vertical load, LFZO — F_x nominal vertical load

1 (default) | positive scalar

Scale factor of the F_x nominal vertical load, λ_FZO. LFZO is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx shape factor, LCX — F_x shape factor

1 (default) | positive scalar

Scale factor of the F_x shape factor, λ_LCX. LCX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx peak friction coefficient, LMUX — F_x peak friction coefficient

1 (default) | positive scalar

Scale factor of the F_x peak friction coefficient, λ_μX. LMUX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx curvature factor, LEX — F_x curvature factor

1 (default) | positive scalar

Scale factor of the F_x curvature factor, λ_EX. LEX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx slip stiffness, LKX — F_x slip stiffness

1 (default) | positive scalar

Scale factor of the F_x slip stiffness, λ_KX. LKX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx horizontal shift, LHX — F_x horizontal shift

1 (default) | positive scalar

Scale factor of the F_x horizontal shift, λ_hX. LHX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx vertical shift, LVX — F_x vertical shift

1 (default) | positive scalar

Scale factor of the F_x vertical shift, λ_VX. LVX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of rolling resistance, LMY — Rolling resistance

1 (default) | positive scalar

Scale factor of the rolling resistance, λ_MY. LMY is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Advanced

Lower boundary of slip denominator, VXLOW — Lower boundary of slip denominator

1 m/s (default) | positive scalar

Lower boundary of slip denominator, V_XLOW. VXLOW is the TIR file identifier.

Velocity threshold — Wheel hub velocity threshold for mathematical slip model

0.1 m/s (default) | positive scalar

Wheel hub velocity, V_th, below which the block smooths the transition to zero.

Minimum valid wheel slip, KPUMIN — Minimum wheel slip threshold

-1.5 (default) | scalar

Minimum valid wheel slip. A negative value represents wheel slip in the reverse rotational direction.

Maximum valid wheel slip, KPUMAX — Maximum wheel slip threshold

1.5 (default) | scalar

Maximum valid wheel slip.

More About

Real-Time and Hardware-in-the-Loop Simulation

For optimal simulation performance, set the Dynamics > Compliance parameter to No compliance - Suitable for HIL simulation.

References

[1] Besselink, I. J.M., A. J.C. Schmeitz, and H. B. Pacejka. “An Improved Magic Formula/Swift Tyre Model That Can Handle Inflation Pressure Changes.” Vehicle System Dynamics 48, no. sup1 (December 2010): 337–52. https://doi.org/10.1080/00423111003748088.

[2] Pacejka, H. B. Tire and Vehicle Dynamics. Elsevier Science, 2005.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2011a

R2024b: Track power dissipated due to tread slip

The block now logs power_dissipated in the simlog workspace variable, which represents power dissipated due to tread slip.

R2023a: Magic Formula compatibility enhancements

You can set Parameterize by to Load-dependent Magic Formula coefficients to enable load-dependent Magic Formula coefficients.

These parameters are new for all parameterizations:

• Lower boundary of slip denominator, VXLOW

• Minimum valid wheel slip, KPUMIN

• Maximum valid wheel slip, KPUMAX