gm2dm
Convert disk-based gain margin to disk size and skew
Description
umargin and
diskmargin
model gain and phase variation as a multiplicative factor
F(s) taking values in a disk centered on the real
axis. The disk is described by two parameters: ɑ, which sets the size of
the variation, and σ, or skew, which biases the gain variation toward
increase or decrease. (See Algorithms for more details about
this model.) The disk can alternatively be described by its real-axis intercepts
DGM = [gmin,gmax], which represent the relative amount of gain
variation around the nominal value F = 1. Use gm2dm
and dm2gm to convert between the
ɑ,σ values and the disk-based gain margin
DGM = [gmin,gmax] that describe the same disk.
Examples
Input Arguments
Output Arguments
Algorithms
umargin and
diskmargin
model gain and phase variations in an individual feedback channel as a frequency-dependent
multiplicative factor F(s) multiplying the nominal
open-loop response L(s), such that the perturbed
response is
L(s)F(s).
The factor F(s) is parameterized by:
In this model,
δ(s) is a gain-bounded dynamic uncertainty, normalized so that it always varies within the unit disk (||δ||∞ < 1).
ɑ sets the amount of gain and phase variation modeled by F. For fixed σ, the parameter ɑ controls the size of the disk. For ɑ = 0, the multiplicative factor is 1, corresponding to the nominal L.
σ, called the skew, biases the modeled uncertainty toward gain increase or gain decrease.
The factor F takes values in a disk centered on the real axis and
containing the nominal value F = 1. The disk is characterized by its
intercept DGM = [gmin,gmax] with the real axis. gmin
< 1 and gmin > 1 are the minimum and maximum relative changes in
gain modeled by F, at nominal phase. The phase uncertainty modeled by
F is the range DPM = [-pm,pm] of phase values at
the nominal gain (|F| = 1). For instance, in the following plot, the
right side shows the disk F that intersects the real axis in the interval
[0.71,1.4]. The left side shows that this disk models a gain variation of ±3 dB and a phase
variation of ±19°.
DGM = [0.71,1.4]
F = umargin('F',DGM)
plot(F)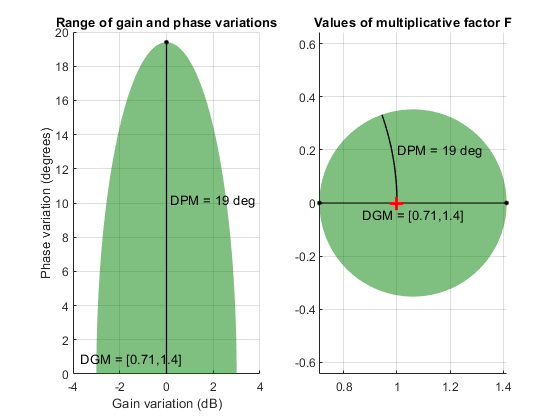
gm2dm and gm2dm converts between these two ways
of specifying a disk of multiplicative gain and phase uncertainty: a gain-variation range of
the form DGM = [gmin,gmax], and the
ɑ,σ parameterization of the corresponding disk.
For further details about the uncertainty model for gain and phase variations, see Stability Analysis Using Disk Margins.
Version History
Introduced in R2020a
See Also
diskmargin | diskmarginplot | dm2gm | getDGM | umargin


