beamdwellfactor
Description
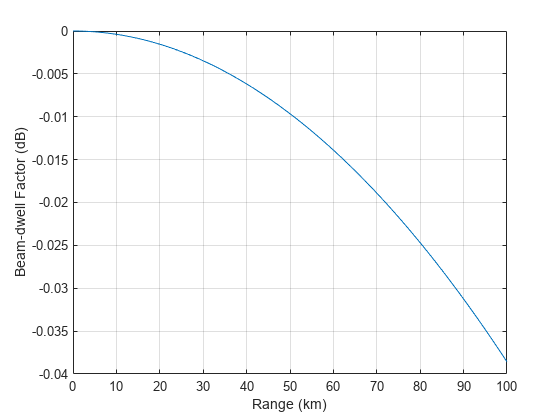
fbd = beamdwellfactor(r,hpbw,scanrate)fbd for an antenna at the specified range r,
half-power beamwidth hpbw, and scan rate scanrate.
The beamdwellfactor function assumes that the transmitter and receiver
antennas have equal beamwidth and an ideal Gaussian antenna pattern with no side
lobes.
Examples
Input Arguments
Output Arguments
More About
References
[1] Barton, David Knox. "Beam-Dwell Factor Fbd." In Radar Equations for Modern Radar, 362. Artech House Radar Series. Boston, Mass: Artech House, 2013.
[2] Barton, David Knox. "Antenna Patterns." In Radar Equations for Modern Radar, 147. Artech House Radar Series. Boston, Mass: Artech House, 2013.
Extended Capabilities
Version History
Introduced in R2021a